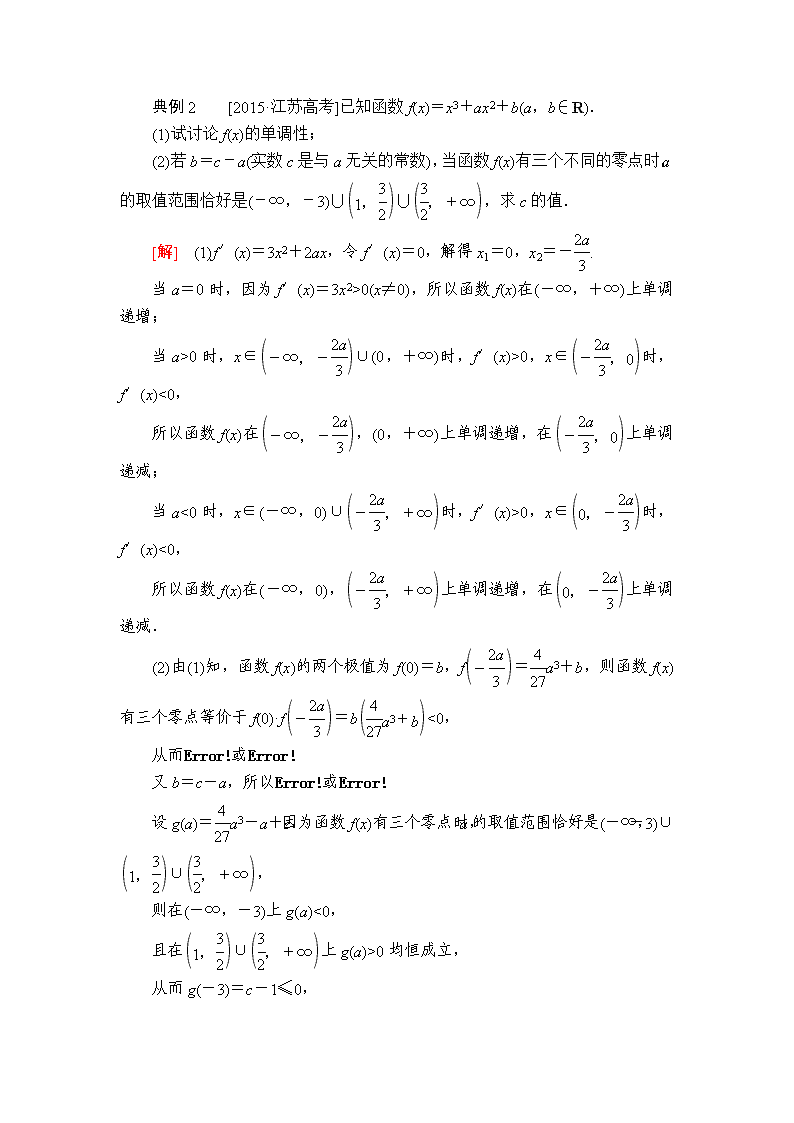2017届高考文科数学(全国通用)二轮文档讲义:第1编专题1-3分类讨论思想
第三讲 分类讨论思想
思想方法解读
考点 由概念、法则、公式引起的分类讨论
典例1 (1)[2015·福建高考]若函数f(x)=(a>0,且a≠1)的值域是[4,+∞),则实数a的取值范围是________.
[解析] 因为f(x)=所以当x≤2时,f(x)≥4;又函数f(x)的值域为[4,+∞),所以解得1
0,因为Sn=(+)2(n≥2),所以=+,即数列{}是以=为首项,以为公差的等差数列,所以=n,所以Sn=n2a1,所以当n≥2时,an=Sn-Sn-1=n2a1-(n-1)2a1=(2n-1)a1,当n=1时,适合上式,
所以bn=+=+=1++1-=2+2,
所以Tn=2n+2=2n+2=2n+=.
[答案]
四步解决由概念、法则、公式引起的分类讨论问题
第一步:确定需分类的目标与对象.即确定需要分类的目标,一般把需要用到公式、定理解决问题的对象作为分类目标.
第二步:根据公式、定理确定分类标准.运用公式、定理对分类对象进行区分.
第三步:分类解决“分目标”问题.对分类出来的“分目标”分别进行处理.
第四步:汇总“分目标”.将“分目标”问题进行汇总,并作进一步处理.
【针对训练1】 在公差为d的等差数列{an}中,已知a1=10,且a1,2a2+2,5a3成等比数列.
(1)求d,an;
(2)若d<0,求|a1|+|a2|+|a3|+…+|an|.
解 (1)由题意得5a3·a1=(2a2+2)2,
即5(a1+2d)·a1=(2a1+2d+2)2
d2-3d-4=0,解得d=-1或d=4,
所以an=-n+11或an=4n+6.
(2)设数列{an}前n项和为Sn,
因为d<0,所以d=-1,an=-n+11,则
由an≥0,即-n+11≥0得n≤11.
所以当n≤11时,an≥0,n≥12时,an<0.
所以n≤11时,|a1|+|a2|+|a3|+…+|an|=Sn=-n2+n;
n≥12时,|a1|+|a2|+…+|a11|+|a12|+…+|an|=a1+a2+…+a11-a12-…-an=S11-(Sn-S11)=-Sn+2S11=n2-n+110.
综上所述,|a1|+|a2|+…+|an|
=
考点 由参数变化引起的分类讨论
典例2 [2015·江苏高考]已知函数f(x)=x3+ax2+b(a,b∈R).
(1)试讨论f(x)的单调性;
(2)若b=c-a(实数c是与a无关的常数),当函数f(x)有三个不同的零点时,a的取值范围恰好是(-∞,-3)∪∪,求c的值.
[解] (1)f′(x)=3x2+2ax,令f′(x)=0,解得x1=0,x2=-.
当a=0时,因为f′(x)=3x2>0(x≠0),所以函数f(x)在(-∞,+∞)上单调递增;
当a>0时,x∈∪(0,+∞)时,f′(x)>0,x∈时,f′(x)<0,
所以函数f(x)在,(0,+∞)上单调递增,在上单调递减;
当a<0时,x∈(-∞,0)∪时,f′(x)>0,x∈时,f′(x)<0,
所以函数f(x)在(-∞,0),上单调递增,在上单调递减.
(2)由(1)知,函数f(x)的两个极值为f(0)=b,f=a3+b,则函数f(x)有三个零点等价于f(0)·f=b<0,
从而或
又b=c-a,所以或
设g(a)=a3-a+c,因为函数f(x)有三个零点时,a的取值范围恰好是(-∞,-3)∪∪,
则在(-∞,-3)上g(a)<0,
且在∪上g(a)>0均恒成立,
从而g(-3)=c-1≤0,
且g=c-1≥0,因此c=1.
此时,f(x)=x3+ax2+1-a=(x+1)[x2+(a-1)x+1-a],
因函数有三个零点,则x2+(a-1)x+1-a=0有两个异于-1的不等实根,
所以Δ=(a-1)2-4(1-a)=a2+2a-3>0,且(-1)2-(a-1)+1-a≠0,
解得a∈(-∞,-3)∪∪.
综上c=1.
1.变量或参数变化时常见的分类讨论
(1)解含参数的不等式时,常按参数的取值不同分类讨论.
(2)平面解析几何中,直线点斜式中按斜率k存在和不存在,直线截距式中按截距b=0和b≠0分类讨论.
2.利用分类讨论思想的注意点
(1)分类讨论要标准统一,层次分明,分类要做到“不重不漏”.
(2)分类讨论时要根据题设条件确定讨论的级别,再确定每级讨论的对象与标准,每级讨论中所分类别应做到与前面所述不重不漏,最后将讨论结果归类合并,其中级别与级别之间有严格的先后顺序、类别和类别之间没有先后;最后整合时要注意是取交集、并集,还是既不取交集也不取并集只是分条列出.
【针对训练2】 [2016·四川高考]设函数f(x)=ax2-a-ln x,其中a∈R.
(1)讨论f(x)的单调性;
(2)确定a的所有可能取值,使得f(x)>-e1-x在区间(1,+∞)内恒成立(e=2.718…为自然对数的底数).
解 (1)f′(x)=2ax-=(x>0).
当a≤0时,f′(x)<0,f(x)在(0,+∞)内单调递减.
当a>0时,由f′(x)=0,有x=.
此时,当x∈时,f′(x)<0,f(x)单调递减;
当x∈时,f′(x)>0,f(x)单调递增.
(2)令g(x)=-,s(x)=ex-1-x.
则s′(x)=ex-1-1.
而当x>1时,s′(x)>0,
所以s(x)在区间(1,+∞)内单调递增.
又由s(1)=0,有s(x)>0,
从而当x>1时,g(x)>0.
当a≤0,x>1时,f(x)=a(x2-1)-ln x<0.
故当f(x)>g(x)在区间(1,+∞)内恒成立时,必有a>0.
当01.
由(1)有f0,
所以此时f(x)>g(x)在区间(1,+∞)内不恒成立.
当a≥时,令h(x)=f(x)-g(x)(x≥1).
当x>1时,h′(x)=2ax-+-e1-x>x-+-=>>0.
因此,h(x)在区间(1,+∞)内单调递增.
又h(1)=0,所以当x>1时,h(x)=f(x)-g(x)>0,即f(x)>g(x)恒成立.
综上,a∈.
考点 根据图形位置或形状分类讨论
典例3 [2015·广东高考]已知过原点的动直线l与圆C1:x2+y2-6x+5=0相交于不同的两点A,B.
(1)求圆C1的圆心坐标;
(2)求线段AB的中点M的轨迹C的方程;
(3)是否存在实数k,使得直线L:y=k(x-4)与曲线C只有一个交点?若存在,求出k的取值范围;若不存在,说明理由.
[解] (1)圆C1的标准方程为(x-3)2+y2=4,圆心坐标为C1(3,0).
(2)由垂径定理知,C1M⊥AB,故点M在以OC1为直径的圆上,即2+y2=.
故线段AB的中点M的轨迹C的方程是2+y2=在圆C1:(x-3)2+y2=4内部的部分,设AB方程为y=k1x,当AB与圆C1相切时⇒(k+1)x2-6x+5=0,
由Δ=36-4×5×(k+1)=0得k1=±,
代入方程组得x=,因此x∈.
即2+y2=.
(3)联立解得
不妨设其交点为P1,P2,
设直线L:y=k(x-4)所过定点为P(4,0),
则kPP1=-,kPP2=.
当直线L与圆C相切时,=,解得k=±.
故当k∈∪时,直线L与曲线C只有一个交点.
六类常见的由图形的位置或形状变化引起的分类讨论
(1)二次函数对称轴的变化;(2)函数问题中区间的变化;(3)函数图象形状的变化;(4)直线由斜率引起的位置变化;(5)圆锥曲线由焦点引起的位置变化或由离心率引起的形状变化;(6)立体几何中点、线、面的位置变化等.
【针对训练3】 (1)设圆锥曲线C的两个焦点分别为F1,F2,若曲线C上存在点P满足|PF1|∶|F1F2|∶|PF2|=4∶3∶2,则曲线C的离心率等于( )
A.或 B.或2
C.或2 D.或
答案 A
解析 不妨设|PF1|=4t,|F1F2|=3t,|PF2|=2t,其中t≠0,若该曲线为椭圆,则有|PF1|+|PF2|=6t=2a,|F1F2|=3t=2c,e====.
若该曲线为双曲线,则有|PF1|-|PF2|=2t=2a,
|F1F2|=3t=2c,e====.
(2)已知变量x,y满足的不等式组表示的是一个直角三角形围成的平面区域,则实数k=( )
A.- B.
C.0 D.-或0
答案 D
解析 不等式组表示的可行域如图(阴影部分)所示,由图可知,若要使不等式组表示的平面区域是直角三角形,只有当直线y=kx+1与直线x=0或y=2x垂直时才满足.
结合图形可知斜率k的值为0或-.