- 2021-06-23 发布 |
- 37.5 KB |
- 16页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
数学·山东省德州市武城二中2016-2017学年高二上学期第一次月考数学试卷 Word版含解析]x
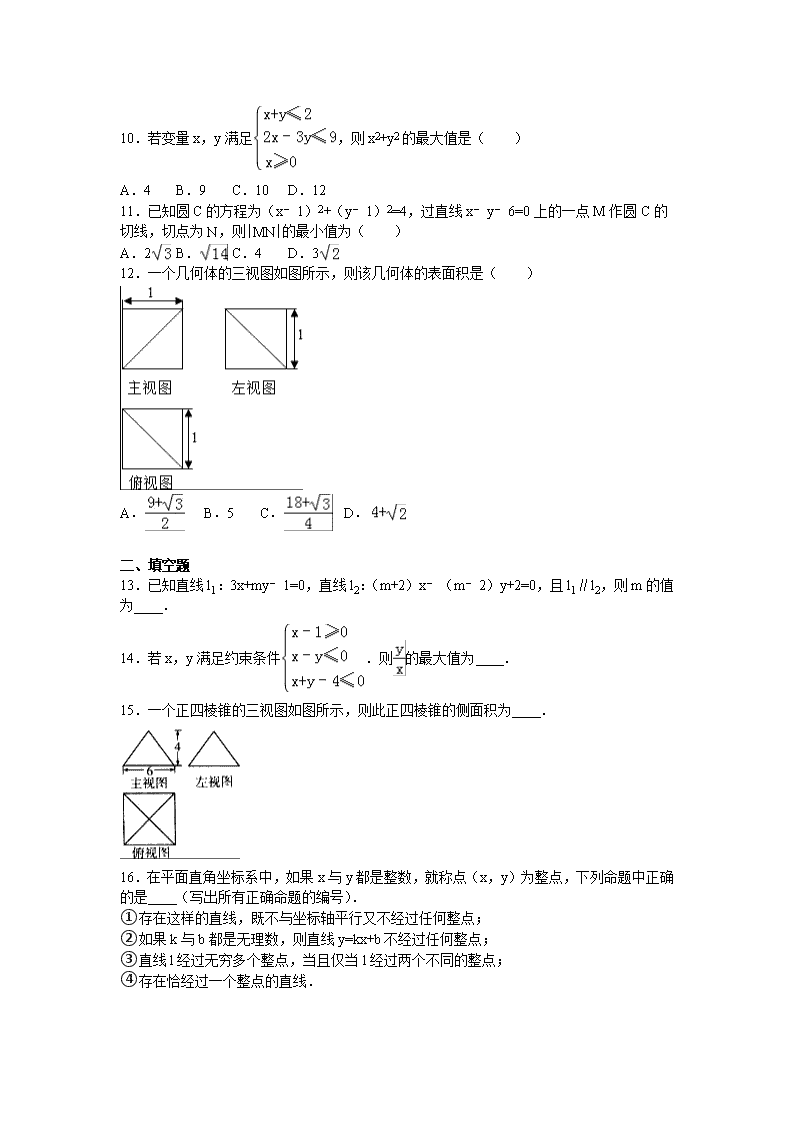
2016-2017学年山东省德州市武城二中高二(上)第一次月考数学试卷 一、选择题 1.过点P(﹣2,m)和Q(m,4)的直线斜率等于1,那么m的值等于( ) A.1或3 B.4 C.1 D.1或4 2.已知a>0,b<0,c>0则直线ax+by+c=0必不经过( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 3.与直线3x﹣4y+5=0关于y轴对称的直线方程是( ) A.3x+4y﹣5=0 B.3x+4y+5=0 C.3x﹣4y+5=0 D.3x﹣4y﹣5=0 4.过点(﹣1,2)且与直线2x﹣3y+4=0垂直的直线方程为( ) A.3x+2y﹣1=0 B.3x+2y+7=0 C.2x﹣3y+5=0 D.2x﹣3y+8=0 5.已知直线l1与圆x2+y2+2y=0相切,且与直线l2:3x+4y﹣6=0平行,则直线l1的方程是( ) A.3x+4y﹣1=0 B.3x+4y+1=0或3x+4y﹣9=0 C.3x+4y+9=0 D.3x+4y﹣1=0或3x+4y+9=0 6.在平面直角坐标系中,不等式组表示的平面区域的面积是( ) A. B.4 C. D.2 7.点A(1,1)到直线xcosθ+ysinθ﹣2=0的距离的最大值是( ) A.1+ B.2+ C.1+ D.2+ 8.已知水平放置的△ABC是按“斜二测画法”得到如图所示的直观图,其中B′O′=C′O′=1,A′O′=,那么原△ABC的面积是( ) A. B. C. D. 9.若直线x+my=2+m与圆x2+y2﹣2x﹣2y+1=0相交,则实数m的取值范围为( ) A.(﹣∞,+∞) B.(﹣∞,0) C.(0,+∞) D.(﹣∞,0)U(0,+∞) 10.若变量x,y满足,则x2+y2的最大值是( ) A.4 B.9 C.10 D.12 11.已知圆C的方程为(x﹣1)2+(y﹣1)2=4,过直线x﹣y﹣6=0上的一点M作圆C的切线,切点为N,则|MN|的最小值为( ) A.2 B. C.4 D.3 12.一个几何体的三视图如图所示,则该几何体的表面积是( ) A. B.5 C. D. 二、填空题 13.已知直线l1:3x+my﹣1=0,直线l2:(m+2)x﹣(m﹣2)y+2=0,且l1∥l2,则m的值为 . 14.若x,y满足约束条件.则的最大值为 . 15.一个正四棱锥的三视图如图所示,则此正四棱锥的侧面积为 . 16.在平面直角坐标系中,如果x与y都是整数,就称点(x,y)为整点,下列命题中正确的是 (写出所有正确命题的编号). ①存在这样的直线,既不与坐标轴平行又不经过任何整点; ②如果k与b都是无理数,则直线y=kx+b不经过任何整点; ③直线l经过无穷多个整点,当且仅当l经过两个不同的整点; ④存在恰经过一个整点的直线. 三、解答题 17.已知直线l1:ax+2y+1=0,直线l2:x﹣y+a=0. (1)若直线l1⊥l2,求a的值及垂足P的坐标; (2)若直线l1∥l2,求a的值及直线l1与l2的距离. 18.已知直线l的方程是y=﹣(a+1)x+2﹣a(a∈R). (1)若l在两坐标轴上的截距相等,求直线l的方程; (2)若l与两坐标轴所围成的三角形的面积为2,求直线l的方程. 19.已知圆C:x2+y2+Dx+Ey+3=0,圆C关于直线x+y﹣1=0对称,圆心在第二象限,半径为 (Ⅰ)求圆C的方程; (Ⅱ)已知不过原点的直线l与圆C相切,且在x轴、y轴上的截距相等,求直线l的方程. 20.已知直线l:4x+3y﹣8=0(a∈R)过圆C:x2+y2﹣ax=0的圆心交圆C于A、B两点,O为坐标原点. (I)求圆C的方程; (II) 求圆C在点P(1,)处的切线方程; (III)求△OAB的面积. 21.某企业生产甲、乙两种产品均需用A,B两种原料,已知生产1吨每种产品所需原料及每天原料的可用限额如表所示,如果生产1吨甲、乙产品可获利润分别为3万元、4万元,则该企业每天可获得最大利润为多少? 甲 乙 原料限额 A(吨) 3 2 12 B(吨) 1 2 8 22.已知过原点的动直线l与圆C1:x2+y2﹣6x+5=0相交于不同的两点A,B. (1)求圆C1的圆心坐标; (2)求线段AB 的中点M的轨迹C的方程; (3)是否存在实数 k,使得直线L:y=k(x﹣4)与曲线 C只有一个交点?若存在,求出k的取值范围;若不存在,说明理由. 2016-2017学年山东省德州市武城二中高二(上)第一次月考数学试卷 参考答案与试题解析 一、选择题 1.过点P(﹣2,m)和Q(m,4)的直线斜率等于1,那么m的值等于( ) A.1或3 B.4 C.1 D.1或4 【考点】直线的斜率. 【分析】利用直线的斜率公式求解. 【解答】解:∵过点P(﹣2,m)和Q(m,4)的直线斜率等于1, ∴k==1, 解得m=1. 故选:C. 2.已知a>0,b<0,c>0则直线ax+by+c=0必不经过( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 【考点】直线的一般式方程. 【分析】化方程为斜截式方程,由斜率和截距的意义可得. 【解答】解:由题意可知a>0,b<0,c>0, 直线方程可化为y=x﹣, ∴直线的斜率>0,截距>0, ∴直线ax+by+c=0必不经过第四象限, 故选:D. 3.与直线3x﹣4y+5=0关于y轴对称的直线方程是( ) A.3x+4y﹣5=0 B.3x+4y+5=0 C.3x﹣4y+5=0 D.3x﹣4y﹣5=0 【考点】与直线关于点、直线对称的直线方程. 【分析】令x=0,可得直线3x﹣4y+5=0与y轴的交点.令y=0,可得直线3x﹣4y+5=0与x轴的交点,此点关于y轴的对称点为.可得:与直线3x﹣4y+5=0关于y轴对称的直线经过两点:,.利用截距式即可得出. 【解答】解:令x=0,则y=,可得直线3x﹣4y+5=0与y轴的交点. 令y=0,可得x=﹣,可得直线3x﹣4y+5=0与x轴的交点,此点关于y轴的对称点为. ∴与直线3x﹣4y+5=0关于y轴对称的直线经过两点:,. 其方程为: =1,化为:3x+4y﹣5=0. 故选:A. 4.过点(﹣1,2)且与直线2x﹣3y+4=0垂直的直线方程为( ) A.3x+2y﹣1=0 B.3x+2y+7=0 C.2x﹣3y+5=0 D.2x﹣3y+8=0 【考点】直线的一般式方程与直线的垂直关系. 【分析】根据与已知直线垂直的直线系方程可设与直线2x﹣3y+4=0垂直的直线方程为﹣3x﹣2y+c=0,再把点(﹣1,2)代入,即可求出c值,得到所求方程. 【解答】解:∵所求直线方程与直线2x﹣3y+4=0垂直,∴设方程为﹣3x﹣2y+c=0 ∵直线过点(﹣1,2),∴﹣3×(﹣1)﹣2×2+c=0 ∴c=1 ∴所求直线方程为3x+2y﹣1=0. 故选:A. 5.已知直线l1与圆x2+y2+2y=0相切,且与直线l2:3x+4y﹣6=0平行,则直线l1的方程是( ) A.3x+4y﹣1=0 B.3x+4y+1=0或3x+4y﹣9=0 C.3x+4y+9=0 D.3x+4y﹣1=0或3x+4y+9=0 【考点】直线与圆的位置关系;直线的一般式方程与直线的平行关系. 【分析】由直线的一般式方程与直线的平行关系,设出直线l1的方程为3x+4y+m=0,再由直线l1与圆相切,得到圆心到直线的距离等于圆的半径,利用点到直线的距离公式列出关于m的方程,求出方程的解得到m的值,即可确定出直线l1的方程. 【解答】解:∵直线l1与直线l2:3x+4y﹣6=0平行, ∴设直线l1为3x+4y+m=0, 将圆的方程化为x2+(y+1)2=1,得到圆心坐标为(0,﹣1),半径r=1, 又直线l1与圆x2+y2+2y=0相切, ∴圆心到3x+4y+m=0的距离d=r,即=1, 解得:m=9或m=﹣1, 则直线l1的方程为3x+4y﹣1=0或3x+4y+9=0. 故选D 6.在平面直角坐标系中,不等式组表示的平面区域的面积是( ) A. B.4 C. D.2 【考点】简单线性规划的应用. 【分析】本题考查的知识点是线性规划,处理的思路为:根据已知的约束条件对应的可行域,分析满足条件的图形的形状,结合三角形面积的求法,即可求解. 【解答】解:由已知易得满足约束条件的可行域即为△ABC, 又∵, 故选B. 7.点A(1,1)到直线xcosθ+ysinθ﹣2=0的距离的最大值是( ) A.1+ B.2+ C.1+ D.2+ 【考点】点到直线的距离公式. 【分析】利用点到直线的距离公式、两角和差的正弦关系及其正弦函数的单调性即可得出. 【解答】解:点A(1,1)到直线xcosθ+ysinθ﹣2=0的距离d==, 当且仅当=﹣1时d取得最大值,d=. 故选:B. 8.已知水平放置的△ABC是按“斜二测画法”得到如图所示的直观图,其中B′O′=C′O′=1,A′O′=,那么原△ABC的面积是( ) A. B. C. D. 【考点】斜二测法画直观图. 【分析】由直观图和原图的面积之间的关系直接求解即可. 【解答】解:因为, 且若△A′B′C′的面积为×2××=, 那么△ABC的面积为 故选A. 9.若直线x+my=2+m与圆x2+y2﹣2x﹣2y+1=0相交,则实数m的取值范围为( ) A.(﹣∞,+∞) B.(﹣∞,0) C.(0,+∞) D.(﹣∞,0)U(0,+∞) 【考点】直线与圆相交的性质. 【分析】直线l:x+my=2+m通过整理,发现它虽然在动,但是经过定点M(2,1),再将点M(2,1)代入圆x2+y2﹣2x﹣2y+1=0方程,发现点M恰好在圆上,因此可得直线l只要与圆不相切,就能与圆相交,从而满足题意.因此求出直线与圆相切时的m值,再求对立面即得实数m的取值范围. 【解答】解:∵直线l:x+my=2+m整理,得x﹣2+m(y﹣1)=0, ∴动直线l经过定点M(2,1), ∵圆x2+y2﹣2x﹣2y+1=0化成标准方程,得(x﹣1)2+(y﹣1)2=1 ∴圆心坐标为C(1,1),半径r=1 又∵点M(2,1)满足(2﹣1)2+(1﹣1)2=1,恰好在圆C上, ∴当直线l与圆C不相切时,必定有l与圆C相交 若直线l与圆C相切,有,可得m=0 因此,可得当m≠0时,总有l与圆C相交 故选D 10.若变量x,y满足,则x2+y2的最大值是( ) A.4 B.9 C.10 D.12 【考点】简单线性规划. 【分析】由约束条件作出可行域,然后结合x2+y2的几何意义,即可行域内的动点与原点距离的平方求得x2+y2的最大值. 【解答】解:由约束条件作出可行域如图, ∵A(0,﹣3),C(0,2), ∴|OA|>|OC|, 联立,解得B(3,﹣1). ∵, ∴x2+y2的最大值是10. 故选:C. 11.已知圆C的方程为(x﹣1)2+(y﹣1)2=4,过直线x﹣y﹣6=0上的一点M作圆C的切线,切点为N,则|MN|的最小值为( ) A.2 B. C.4 D.3 【考点】圆的切线方程. 【分析】求出C(1,1)到直线x﹣y﹣6=0的距离d,可得|MN|的最小值. 【解答】解:圆C的方程为(x﹣1)2+(y﹣1)2=4,圆心坐标为(1,1),半径为2. 要使|MN|最小,需圆心C(1,1)到直线x﹣y﹣6=0的M的距离最小, 而CM的最小值即圆心C(1,1)到直线x﹣y﹣6=0的距离d==3, 故|MN|的最小值为=, 故选:B. 12.一个几何体的三视图如图所示,则该几何体的表面积是( ) A. B.5 C. D. 【考点】由三视图求面积、体积. 【分析】几何体为边长为1的正方体切去一个三棱锥得到的,共含有7个面. 【解答】解:由三视图可知该几何体为边长为1的正方体切去一个三棱锥得到的,三棱锥的底面边长为正方体相邻三个面的对角线长, 剩余几何体有3个面为原正方体的面,有3个面为原正方体面的一半,有1个面为等边三角形,边长为原正方体的面对角线长. ∴几何体的表面积为1×3++()2=. 故选A. 二、填空题 13.已知直线l1:3x+my﹣1=0,直线l2:(m+2)x﹣(m﹣2)y+2=0,且l1∥l2,则m的值为 1或﹣6 . 【考点】直线的一般式方程与直线的平行关系. 【分析】根据直线平行的等价条件进行求解即可得到结论. 【解答】解:若l1∥l2, 则m(m+2)+3(m﹣2)=0, 解得:m=1或﹣6, 故答案为:1或﹣6. 14.若x,y满足约束条件.则的最大值为 3 . 【考点】简单线性规划. 【分析】作出不等式组对应的平面区域,利用目标函数的几何意义,利用数形结合确定的最大值. 【解答】解:作出不等式组对应的平面区域如图:(阴影部分ABC). 设k=,则k的几何意义为区域内的点到原点的斜率, 由图象知OA的斜率最大, 由,解得,即A(1,3), 则kOA==3, 即的最大值为3. 故答案为:3. 15.一个正四棱锥的三视图如图所示,则此正四棱锥的侧面积为 60 . 【考点】由三视图求面积、体积. 【分析】根据三视图可得四棱锥为正四棱锥,判断底面边长与高的数据,求出四棱锥的斜高,代入棱锥的侧面积公式计算. 【解答】解:由三视图知:此四棱锥为正四棱锥,底面边长为6,高为4, 则四棱锥的斜高为=5, ∴四棱锥的侧面积为S==60. 故答案为:60. 16.在平面直角坐标系中,如果x与y都是整数,就称点(x,y)为整点,下列命题中正确的是 ①③④ (写出所有正确命题的编号). ①存在这样的直线,既不与坐标轴平行又不经过任何整点; ②如果k与b都是无理数,则直线y=kx+b不经过任何整点; ③直线l经过无穷多个整点,当且仅当l经过两个不同的整点; ④存在恰经过一个整点的直线. 【考点】命题的真假判断与应用;确定直线位置的几何要素. 【分析】逐项判断即可.①举例说明即可;②举反例即可判断;③说明当直线l经过两个整点时直线l经过无穷多个整点时关键;④举例说明即可得到该命题正确. 【解答】解:①如直线,该直线不经过任何整点,因为当x为整数时,y都是无理数,故①正确; ②取k=,b=﹣都是无理数,但直线经过整点(1,0),故此②错误; ③当直线经过无穷多过整点时肯定经过两个整点,当直线经过两个整点时,设两整点的坐标为(m,n),(p,q),且m≠p,n≠q,则直线方程为,当x=k (m﹣p)+m,k∈Z时,y=k(n﹣q)+n∈Z,即直线经过整点(k(m﹣p)+m,k(n﹣q)+n),k∈Z,k每取一个整数就对应一整点,所以直线经过无穷多个整点,故③正确; ④若直线方程为,直线经过整点(0,0),当x取不为零的任意整数时,y都是无理数,故该直线仅经过整点(0,0),故④正确. 综上可知,答案为:①③④. 三、解答题 17.已知直线l1:ax+2y+1=0,直线l2:x﹣y+a=0. (1)若直线l1⊥l2,求a的值及垂足P的坐标; (2)若直线l1∥l2,求a的值及直线l1与l2的距离. 【考点】直线的一般式方程与直线的平行关系;直线的一般式方程与直线的垂直关系. 【分析】(1)由垂直可得a×1+2×(﹣1)=0,解得a值可得直线的方程,联立方程可解交点坐标; (2)当直线l1∥l2时,,解得a值可得直线的方程,由平行线间的距离公式可得答案. 【解答】解:(1)∵直线l1:ax+2y+1=0,直线l2:x﹣y+a=0, 当直线l1⊥l2时,a×1+2×(﹣1)=0, 解得a=2, ∴l1:2x+2y+1=0,直线l2:x﹣y+2=0, 联立解得 ∴a的值为2,垂足P的坐标为(,); (2)当直线l1∥l2时,, 解得a=﹣2, ∴l1:﹣2x+2y+1=0,直线l2:﹣2x+2y+4=0, 由平行线间的距离公式可得d== ∴a的值为﹣2,直线l1与l2的距离为 18.已知直线l的方程是y=﹣(a+1)x+2﹣a(a∈R). (1)若l在两坐标轴上的截距相等,求直线l的方程; (2)若l与两坐标轴所围成的三角形的面积为2,求直线l的方程. 【考点】直线的截距式方程;三角形的面积公式. 【分析】(1)依题意,由=a﹣2即可求得a,从而可得直线l的方程; (2)设所围成的面积为S,列出S的表达式,利用S=2即可求得参数a的值,从而得到所求直线的方程. 【解答】解:(1)依题意a+1≠0, ∴=a﹣2, ∴a=2,或a=0, ∴所求的直线方程是3x+y=0,或x+y﹣2=0. (2)设所围成的面积为S,则S=•|a﹣2|=2, ∴(a﹣2)2=4|a+1|,解得a=8,或a=0, ∴所求直线方程是x+y﹣2=0,或9x+y+6=0. 19.已知圆C:x2+y2+Dx+Ey+3=0,圆C关于直线x+y﹣1=0对称,圆心在第二象限,半径为 (Ⅰ)求圆C的方程; (Ⅱ)已知不过原点的直线l与圆C相切,且在x轴、y轴上的截距相等,求直线l的方程. 【考点】圆的标准方程;圆的切线方程. 【分析】(Ⅰ)由圆的方程写出圆心坐标,因为圆C关于直线x+y﹣1=0对称,得到圆心在直线上代入得到①,把圆的方程变成标准方程得到半径的式子等于得到②,①②联立求出D和E,即可写出圆的方程; (Ⅱ)设l:x+y=a,根据圆心到切线的距离等于半径列出式子求出a即可. 【解答】解:(Ⅰ)由x2+y2+Dx+Ey+3=0知圆心C的坐标为(﹣,﹣) ∵圆C关于直线x+y﹣1=0对称 ∴点(﹣,﹣)在直线x+y﹣1=0上 即D+E=﹣2,①且=2② 又∵圆心C在第二象限∴D>0,E<0 由①②解得D=2,E=﹣4 ∴所求圆C的方程为:x2+y2+2x﹣4y+3=0 (Ⅱ)∵切线在两坐标轴上的截距相等且不为零,设l:x+y=a ∵圆C:(x+1)2+(y﹣2)2=2 ∴圆心C(﹣1,2)到切线的距离等于半径, 即||=,∴a=﹣1或a=3 所求切线方程x+y=﹣1或x+y=3 20.已知直线l:4x+3y﹣8=0(a∈R)过圆C:x2+y2﹣ax=0的圆心交圆C于A、B两点,O为坐标原点. (I)求圆C的方程; (II) 求圆C在点P(1,)处的切线方程; (III)求△OAB的面积. 【考点】正弦定理;点到直线的距离公式;圆的一般方程;圆的切线方程. 【分析】(I)圆C:x2+y2﹣ax=0的圆心为(,0),将圆心坐标代入4x+3y﹣8=0即可求得a,从而可得圆C的方程; (II)将点P(1,)的坐标代入x2+y2﹣4x=0成立,即点P(1,)在x2+y2﹣4x=0上,设过点P(1,)的切线l1的斜率为k,利用kPC•k=﹣1可求得k,从而可得切线l1的方程; (III)由题意可知,|AB|为圆x2+y2﹣4x=0的直径,其长度为4,利用点到直线的距离公式可求得原点(0,0)到直线l:4x+3y﹣8=0的距离,从而可求△OAB的面积. 【解答】解:(I)∵圆C:x2+y2﹣ax=0的圆心为(,0)… 直线l:4x+3y﹣8=0过圆C的圆心, ∴4×+3×0﹣8=0, ∴a=4… ∴圆C的方程为:x2+y2﹣4x=0… (II)∵点P(1,)在x2+y2﹣4x=0上,且圆心为(2,0)… ∴设过点P(1,)的切线l1的斜率为k,过P、C两点的 直线的斜率为kPC,则 … kPC=… ∵PC⊥l1 ∴kPC•k=﹣1,故k=… ∴切线l1的方程为y﹣=(x﹣1),即x﹣y+2=0… (III)∵圆C:x2+y2﹣4x=0的半径为2,… ∴|BA|=2r=4… 点O(0,0)到直线l:4x+3y﹣8=0的距离为d==… ∴S△OAB=|ABC|•d=×4×=… 21.某企业生产甲、乙两种产品均需用A,B两种原料,已知生产1吨每种产品所需原料及每天原料的可用限额如表所示,如果生产1吨甲、乙产品可获利润分别为3万元、4万元,则该企业每天可获得最大利润为多少? 甲 乙 原料限额 A(吨) 3 2 12 B(吨) 1 2 8 【考点】简单线性规划. 【分析】设每天生产甲乙两种产品分别为x,y吨,利润为z元,然后根据题目条件建立约束条件,得到目标函数,画出约束条件所表示的区域,然后利用平移法求出z的最大值. 【解答】解:设每天生产甲乙两种产品分别为x,y吨,利润为z元, 则, 目标函数为 z=3x+4y. 作出二元一次不等式组所表示的平面区域(阴影部分)即可行域. 由z=3x+4y得y=﹣x+, 平移直线y=﹣x+,由图象可知当直线y=﹣x+, 经过点B时,直线y=﹣x+的截距最大, 此时z最大, 解方程组, 解得:, 即B的坐标为x=2,y=3, ∴zmax=3x+4y=6+12=18. 则每天生产甲乙两种产品分别为2,3吨,能够产生最大的利润,最大的利润是18万元. 22.已知过原点的动直线l与圆C1:x2+y2﹣6x+5=0相交于不同的两点A,B. (1)求圆C1的圆心坐标; (2)求线段AB 的中点M的轨迹C的方程; (3)是否存在实数 k,使得直线L:y=k(x﹣4)与曲线 C只有一个交点?若存在,求出k的取值范围;若不存在,说明理由. 【考点】轨迹方程;直线与圆的位置关系. 【分析】(1)通过将圆C1的一般式方程化为标准方程即得结论; (2)设当直线l的方程为y=kx,通过联立直线l与圆C1的方程,利用根的判别式大于0、韦达定理、中点坐标公式及参数方程与普通方程的相互转化,计算即得结论; (3)通过联立直线L与圆C1的方程,利用根的判别式△=0及轨迹C的端点与点(4,0)决定的直线斜率,即得结论. 【解答】解:(1)∵圆C1:x2+y2﹣6x+5=0, 整理,得其标准方程为:(x﹣3)2+y2=4, ∴圆C1的圆心坐标为(3,0); (2)设当直线l的方程为y=kx、A(x1,y1)、B(x2,y2), 联立方程组, 消去y可得:(1+k2)x2﹣6x+5=0, 由△=36﹣4(1+k2)×5>0,可得k2< 由韦达定理,可得x1+x2=, ∴线段AB的中点M的轨迹C的参数方程为,其中﹣<k<, ∴线段AB的中点M的轨迹C的方程为:(x﹣)2+y2=,其中<x≤3; (3)结论:当k∈(﹣,)∪{﹣, }时,直线L:y=k(x﹣4)与曲线C只有一个交点. 理由如下: 联立方程组, 消去y,可得:(1+k2)x2﹣(3+8k2)x+16k2=0, 令△=(3+8k2)2﹣4(1+k2)•16k2=0,解得k=±, 又∵轨迹C的端点(,±)与点(4,0)决定的直线斜率为±, ∴当直线L:y=k(x﹣4)与曲线C只有一个交点时, k的取值范围为(﹣,)∪{﹣, }. 2016年11月29日查看更多