数学理卷·2018届陕西省黄陵中学高三（重点班）上学期期末考试（2018

数学理卷·2018届陕西省黄陵中学高三（重点班）上学期期末考试（2018

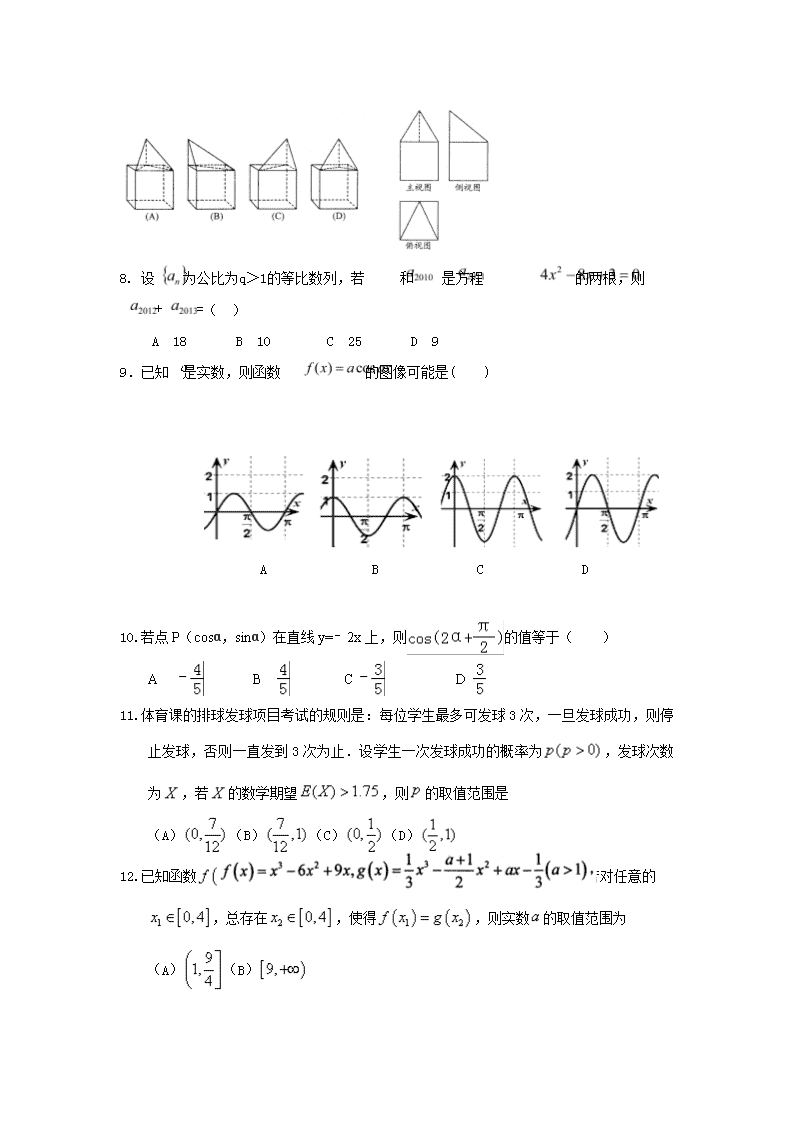
高三重点班期末考试 数学试题（理）‎ 一、选择题: 本大题共12小题, 每小题5分, 在每小题给出的四个选项中，只有一项是符合题目要求的.【来源：全,品…中&高*考+网】1. 如果复数是实数，则实数( )‎ A.      B. 1 C.    D. ‎ ‎2. 集合，，则（ ）‎ A． B． C． D． ‎ ‎3. 已知向量 若，则（ ）‎ A. 1       B.       C.       D.2‎ ‎4. 已知 则（　　 ） ‎ A.   B.   C.   D. ‎ ‎5. 函数是定义在R上的奇函数，对任意两个不相等的正数，都有,记，则（ ）‎ A. B. C. D. ‎ ‎6．已知数列{}满足，且，‎ 则的值是（ ）‎ A B C 5 D ‎ ‎7. —空间几何体的三视图如图所示，则此空间几何体的直观图为（ ）‎ ‎8. 设 为公比为q＞1的等比数列，若 和 是方程 的两根，则 ‎ + =（ ）‎ A 18 B 10 C 25 D 9‎ ‎9．已知 是实数，则函数 的图像可能是( )‎ A B C D ‎10.若点P（cosα，sinα）在直线y=﹣2x上，则的值等于（　　）‎ A B C D ‎ ‎11.体育课的排球发球项目考试的规则是：每位学生最多可发球3次，一旦发球成功，则停止发球，否则一直发到3次为止．设学生一次发球成功的概率为，发球次数为，若的数学期望，则的取值范围是 ‎（A）（B）（C）（D）‎ ‎12.已知函数，若对任意的，总存在，使得，则实数的取值范围为 ‎（A）（B）‎ ‎（C）（D）‎ 二、 填空题：本大题共4小题，每小题5分。‎ ‎13、在等比数列{an}中，若，则     ‎ ‎14.已知，若是的充分条件，则实数的取值范围是____．‎ ‎15. 若函数满足且时，，函数，则实数在区间内零点的个数为 .‎ ‎16．如图，PA⊥圆O所在的平面，AB是圆O的直径，C是圆O上的一点，E、F分别是点A在PB、PC上的射影，给出下列结论：‎ ‎①AF⊥PB；②EF⊥PB；③AF⊥BC；④AE⊥平面PBC；⑤．‎ 其中正确命题的序号是 ．‎ 三、解答题（70分）‎ ‎17. （本题满分12分）‎ 在中，角A，B,C的对边分别是且满足 ‎（Ⅰ）求角B的大小；（Ⅱ）若的面积为为，求的值.‎ ‎18.（本题满分12分）【来源：全,品…中&高*考+网】设数列，其前项和，为单调递增的等比数列，，.‎ ‎（Ⅰ）求数列的通项公式；‎ ‎（Ⅱ）若，数列的前项和，求证：.‎ ‎19．（满分12分）如图，在四棱锥P﹣ABCD中，底面ABCD为直角梯形，AD∥BC，∠ADC=90°PA=PD=AD=2BC=2，CD=，Q是AD的中点，M是棱PC上的点，且PM=3MC．‎ ‎（Ⅰ）求证：平面PAD⊥底面ABCD；‎ ‎（Ⅱ）求二面角M﹣BQ﹣C的大小．‎ ‎20. （本小题满分12分）‎ 如图，在平面直角坐标系中，已知是椭圆上的一点，从原点向圆作两条切线，分别交椭圆于点．‎ ‎（1）若点在第一象限，且直线互相垂直，求圆的方程；‎ ‎（2）若直线的斜率存在，并记为，求的值；‎ ‎21.（本小题满分12分）已知函数，曲线在点处的切线方程为：.‎ ‎（Ⅰ）求，的值；‎ ‎（Ⅱ）设，求函数在上的最大值.‎ ‎22.（本小题10分）‎ 已知平面直角坐标系中，以为极点，轴的非负半轴为极轴建立极坐标系，点极坐标为，曲线的极坐标方程为（为参数）．‎ ‎（1）写出点的直角坐标及曲线的直角坐标方程；‎ ‎（2）若为曲线上的动点，求的中点到直线：的距离的最小值．‎ ‎ ‎ 一、 A B D D C B A A C B C C 13、 ‎14. ‎ 15. ‎8 ‎ ‎16．①②③⑤‎ 二、解答题 ‎17. 解：（1）∵，∴【来源：全,品…中&高*考+网】∴‎ ‎∵，∴‎ 又∵‎ ‎(2)，‎ ‎∴…………12分 ‎18. 解：(1)当时，，‎ 当时，，当时，也满足，∴，∵等比数列，∴，‎ ‎∴，又∵，‎ ‎∴或（舍去），‎ ‎∴（4分）；‎ ‎（2）由（1）可得：，∴‎ ‎，显然数列是递增数列，∴，即.(12分）‎ ‎19.（Ⅰ）证明：连结BQ，∵四边形ABCD是直角梯形，AD∥BC，AD=2BC，Q为AD的中点，‎ ‎∴四边形ABDQ为平行四边形，又∵CD=，∴QB=，∵△PAD是边长为2的正三角形，Q是AD的中点，∴PQ⊥AD，PQ=，在△PQB中，QB=，PB=，有PQ2+BQ2=PB2，∴PQ⊥BQ，∵AD∩BQ=Q，AD、BQ⊂平面ABCD，∴PQ⊥平面ABCD，又∵PQ⊂平面PAD，∴平面PAD⊥底面ABCD；（Ⅱ）解：由（I）可知能以Q为原点，分别以QA、QB、QP为x、y、z轴建立坐标系如图，则Q（0，0，0），B（0，，0），∵BC=1，CD=，Q是AD的中点，∴PQ===，QC===2，‎ ‎∴PC===，又∵PM=3MC，∴M（﹣，，），‎ ‎∴=（0，，0），=（﹣，，），设平面MBQ的一个法向量为=（x，y，z），‎ 由，即，令z=，得=（1， 0，），‎ 又=（0，0，1）为平面BCQ的一个法向量，∴==，‎ ‎∴二面角M﹣BQ﹣C为．‎ ‎20．（1）由圆的方程知圆的半径，因为直线互相垂直，且和圆相切，所以，即 ①又点在椭圆上，所以 ②‎ 联立①②，解得，所以，所求圆的方程为．　‎ ‎（2）因为直线和都与圆相切，所以，‎ ‎，化简得，因为点在椭圆上，所以，‎ 即，所以．‎ 21. ‎（本小题12分）‎ 解：（Ⅰ）由切线方程知，当时，‎ ‎∴....................................................1分 ‎∵....................................................2分 ‎∴由切线方程知，.......................................3分 ‎∴..........................................................4分 ‎（Ⅱ）由（Ⅰ）知，.......................5分 ‎∴，.........................................6分 当时，当时，，故单调递减 ‎∴在上的最大值为.........................................7分 ‎②当时 ‎∵，‎ ‎∴存在，使 当时，，故单调递减 当时，，故单调递增 ‎∴在上的最大值为或....................................9分 又，‎ ‎∴当时，在上的最大值为 当时，在上的最大值为......................10分 ƒ当时，当时，，故单调递增 ‎∴在上的最大值为..................................11分 综上所述，当时，在上的最大值为 当时，在上的最大值为.........................12分 ‎22.（本小题10分）‎ 解：（1）点的直角坐标为．‎ 由，得，①‎ 将，，代入①，‎ 可得曲线的直角坐标方程为．‎ ‎（2）直线：的直角坐标方程为，‎ 设点的直角坐标为，则，‎ 那么到直线的距离 ‎，‎ ‎∴（当且仅当时取等号），‎ 所以到直线：的距离的最小值为．‎