数学卷·2018届天津市六校（宝坻一中、静海一中等）高二上学期期中联考（2016-11）

数学卷·2018届天津市六校（宝坻一中、静海一中等）高二上学期期中联考（2016-11）

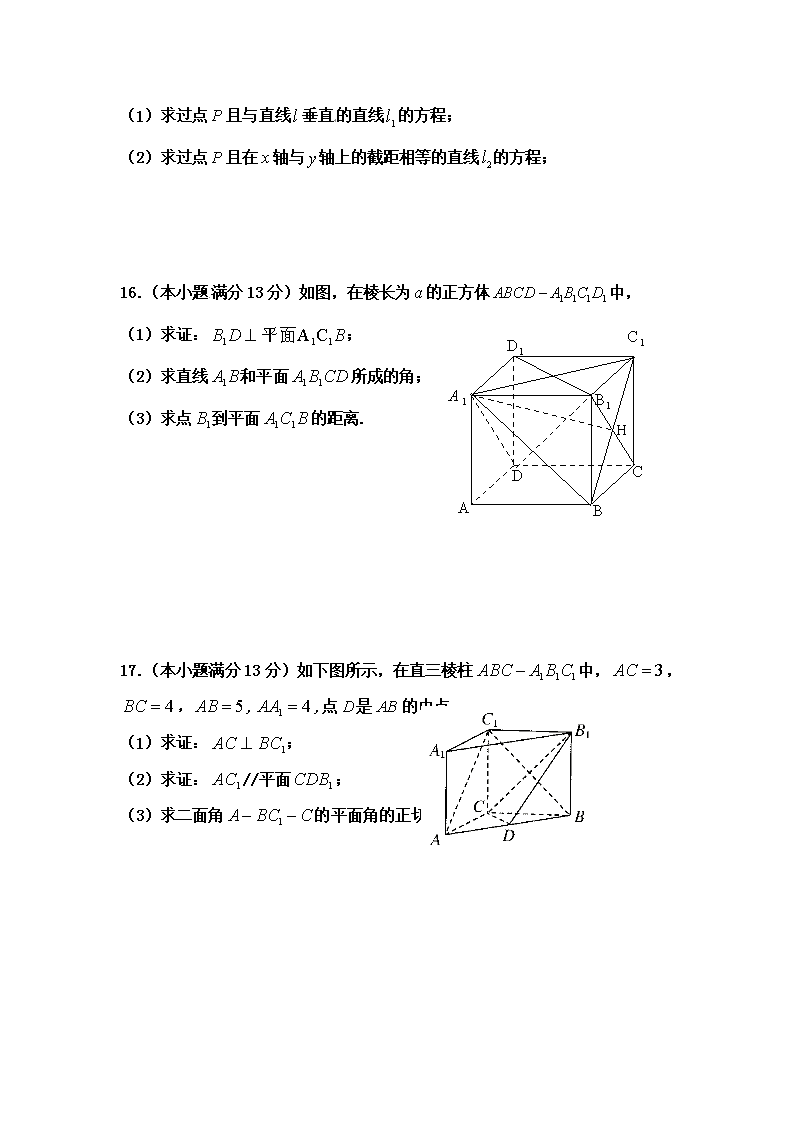
‎2016-2017学年度第一学期期中六校联考高二数学试卷 ‎（考试时间：120分钟 满分：150分） ‎ Ⅰ、选择题（本大题共8小题，每小题5分，共40分）‎ ‎1．点是点在坐标平面内的射影，则等于 （ ）‎ ‎ （A） （B） （C） （D）‎ ‎2．用斜二测画法画边长为1的正方形的直观图，则直观图的面积是（ ）‎ ‎ （A）1 （B） （C） （D）‎ ‎3．若直线与平行，则与间的距离为 （ ）‎ ‎ （A） （B） （C） （D）‎ ‎4．一个几何体的三视图如图所示，则该几何体的体积为 （ ）‎ ‎ （A） （B） ‎ ‎ （C） （D）‎ ‎5．已知底面边长为1，侧棱长为的正四棱柱的各顶点均在同一个球面上，则该球的体积为 （ ）‎ ‎ （A） （B） （C） （D）‎ ‎6．设是两个不同的平面，是一条直线，以下命题：‎ ‎ ①若，则∥； ②若∥，∥，则∥；‎ ‎ ③若，∥，则； ④若∥，，则.‎ 其中正确命题的个数是 （ ）‎ ‎ （A）1个 （B）2个 （C）3个 （D）4个 ‎7．若直线过圆的圆心，则 的取值范围是 （ ）‎ ‎ （A） （B） （C） （D）‎ ‎8．过点作圆的弦，其中弦长为整数的共有 （ ）‎ ‎ （A）16条 （B）17条 （C）32条 （D）34条 Ⅱ、填空题（本大题共6小题，每小题5分，共30分）‎ ‎9．已知圆的方程为,则过点的圆的切线方程为 ▲ .‎ ‎10．长方体中，，，则异面直线与所成角的余弦值为 ▲ .‎ ‎11．若直线与直线互相垂直,则实数=‎ ‎ ▲ .‎ ‎12．一个圆锥的表面积为，且它的侧面展开图是一个半圆，则圆锥的底面半径为 ▲ （）.‎ ‎13．曲线与直线有两个不同的公共点，则实数的范围 ▲ .‎ ‎14．若直线与圆至少有一个交点，则实数的取值范围是 ▲ .‎ Ⅲ、解答题（本大题共6小题，共40分）‎ ‎15．（本小题满分13分）已知直线经过点，且斜率为．‎ ‎（1）求过点且与直线垂直的直线的方程；‎ ‎（2）求过点且在轴与轴上的截距相等的直线的方程；‎ ‎ ‎ ‎16．（本小题满分13分）如图，在棱长为的正方体中， ‎ ‎1‎ H ‎（1）求证：；‎ ‎（2）求直线和平面所成的角； ‎ ‎（3）求点到平面的距离.‎ ‎17．（本小题满分13分）如下图所示，在直三棱柱中，，‎ ‎，,,点是的中点．‎ ‎（1）求证：；‎ ‎（2）求证：//平面；‎ ‎（3）求二面角的平面角的正切值．‎ ‎18．（本小题满分13分）已知圆，直线．‎ ‎（1）判断直线与圆的位置关系；‎ ‎（2）若直线与圆相交于、两点，且，求直线的斜率；‎ ‎（3）若定点P（1，1）分弦为，求此时直线的方程．‎ ‎19．（本小题满分14分）如图，在四棱锥中，为与的交点，平面，是正三角形，//，.‎ ‎（1）求异面直线和所成角的大小；‎ ‎（2）若点为棱上一点，且//平面，求的值；‎ ‎（3）求证：平面平面.‎ ‎20．（本小题满分14分）已知圆:，过定点作斜率为1的直线交圆于、两点，为线段的中点.‎ ‎（1）求的值；‎ ‎（2）设为圆上异于、的一点，求△面积的最大值；‎ ‎（3）从圆外一点向圆引一条切线，切点为，且有 , 求 的最小值，并求取最小值时点的坐标.‎ ‎2016-2017学年度第一学期期中六校联考高二数学试卷 ‎（答题纸） ‎ Ⅰ、选择题（本大题共8小题，每小题5分，共40分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 答案 Ⅱ、填空题（本大题共6小题，每小题5分，共30分）‎ ‎9． 10． 11． ‎ ‎12． 13． 14． ‎ Ⅲ、解答题（本大题共6小题，共40分）‎ ‎15．（本小题满分13分）‎ ‎ ‎ ‎1‎ H ‎16．（本小题满分13分）‎ ‎【来源：全,品…中&高*考+网】‎ ‎17．（本小题满分13分）‎ ‎18．（本小题满分13分）‎ ‎【来源：全,品…中&高*考+网】‎ ‎【来源：全,品…中&高*考+网】‎ ‎19．（本小题满分14分）‎ ‎【来源：全,品…中&高*考+网】‎ ‎20．（本小题满分14分）‎ ‎2016-2017学年度第一学期期中六校联考高二数学试卷 ‎（答案） ‎ Ⅰ、选择题（本大题共8小题，每小题5分，共40分）‎ ‎ 1．A 2．D 3．B 4．A 5．D 6．A 7．B 8．C Ⅱ、填空题（本大题共6小题，每小题5分，共30分）‎ ‎ 9．y=-1或15x+8y-52=0 10． 11．0或-1 ‎ ‎ 12．1 13． 14．（4，+∞）‎ Ⅲ、解答题（本大题共6小题，共40分）‎ ‎15.（本小题满分13分）‎ ‎（1）由已知得，，即直线方程为.……5分 ‎（2）当直线不过原点时，设直线方程为，，即，‎ 直线方程为. ………10分 ‚当直线过原点时，直线斜率为，直线方程为，即.‎ 综上‚，直线的方程为或. ………13分 ‎16. （本小题满分13分）‎ ‎1‎ H ‎（1） DC平面，平面，DC ‎ 又，DC=C，平面 平面，，连接，‎ ‎ DD1平面，平面，【来源：全,品…中&高*考+网】‎ ‎ DD1‎ 又，DD1= D1，平面 平面，‎ 又= C1 ，平面 ………5分 ‎ ‎（2）设＝H，由（1）得：平面，连接，‎ 则是在平面上的射影。‎ 即为直线和平面所成角 在Rt中，=,,== =300 ‎ ‎ 直线和平面所成角为300. ………9分 ‎ (3) 设点到平面的距离为d，‎ 由得：‎ 即： ，d=，即点到平面的距离为 ………13分 ‎17．（本小题满分13分）‎ ‎（1）又∵C1C⊥AC.∴AC⊥平面BCC1B1.‎ ‎∵BC1⊂平面BCC1B，∴AC⊥BC1. ………4分 ‎（2）证明：设CB1与C1B的交点为E，连接DE，又四边形BCC1B1为正方形．‎ ‎∵D是AB的中点，E是BC1的中点，∴DE∥AC1.‎ ‎∵DE⊂平面CDB1，AC1⊄平面CDB1，∴AC1∥平面CDB1. ………8分 ‎（3）由已知可得，‎ 设与交于点，连接，则，，‎ 即为二面角A-BC1-C的平面角.‎ 由（1）可知，在中，.‎ 即二面角A-BC1-C的平面角的正切值为. ………13分 ‎18．（本小题满分13分）‎ ‎（1）由题意可知，圆心C到直线的距离 ‎ ‎ ，所以直线与圆相交. ………4分 ‎（2）圆心C（0,1），C到l的距离d= ∴ ‎ 即m2=1 ∴m=1. 直线l的斜率k=1 ………8分 ‎（3）设，由得，‎ ‎∴，化简的………①‎ 又由消去得……（*）‎ ‎∴ …………②‎ 由①②解得，带入（*）式解得，‎ ‎∴直线的方程为或． ………13分 ‎19．（本小题满分14分）‎ ‎（1）因为//，所以异面直线和所成角即为和所成角.‎ 因为是正三角形，，所以PD=CD.‎ 因为平面，//，所以平面.‎ 因为平面，所以，所以为等腰直角三角形.‎ 所以，即异面直线和所成角为. ………4分 ‎（2）因为 所以，所以． ‎ 因为，‎ 所以.‎ 所以． ………8分 ‎ ‎（3）取的中点，连结．‎ 是正三角形，，所以．‎ 为的中点，所以. ‎ ‎，所以．‎ ‎，所以．‎ 设，在等腰直角三角形中，．‎ 在中，．在直角梯形中，．‎ ‎，点F为PC的中点，所以．在中，． ‎ 在中，由，可知，‎ 所以． 由，‎ 所以．又，所以平面 …14分 ‎20．（本小题满分14分）‎ ‎（1）由题知圆心，又为线段的中点，∴⊥，‎ ‎∴，即，∴． ………4分 ‎（2）由（1）知圆的方程为，∴圆心，半径，‎ 又直线的方程是，‎ ‎∴圆心到直线的距离，．‎ 当⊥时，△面积最大，． …8分 ‎（3）∵⊥，∴，又，∴．‎ 设，则有，整理得，即点在 上，∴的最小值即为的最小值，‎ 由解得∴满足条件的点坐标为． …14分