安徽省滁州市定远县民族中学2019-2020学年高二上学期期中考试数学（文）试题

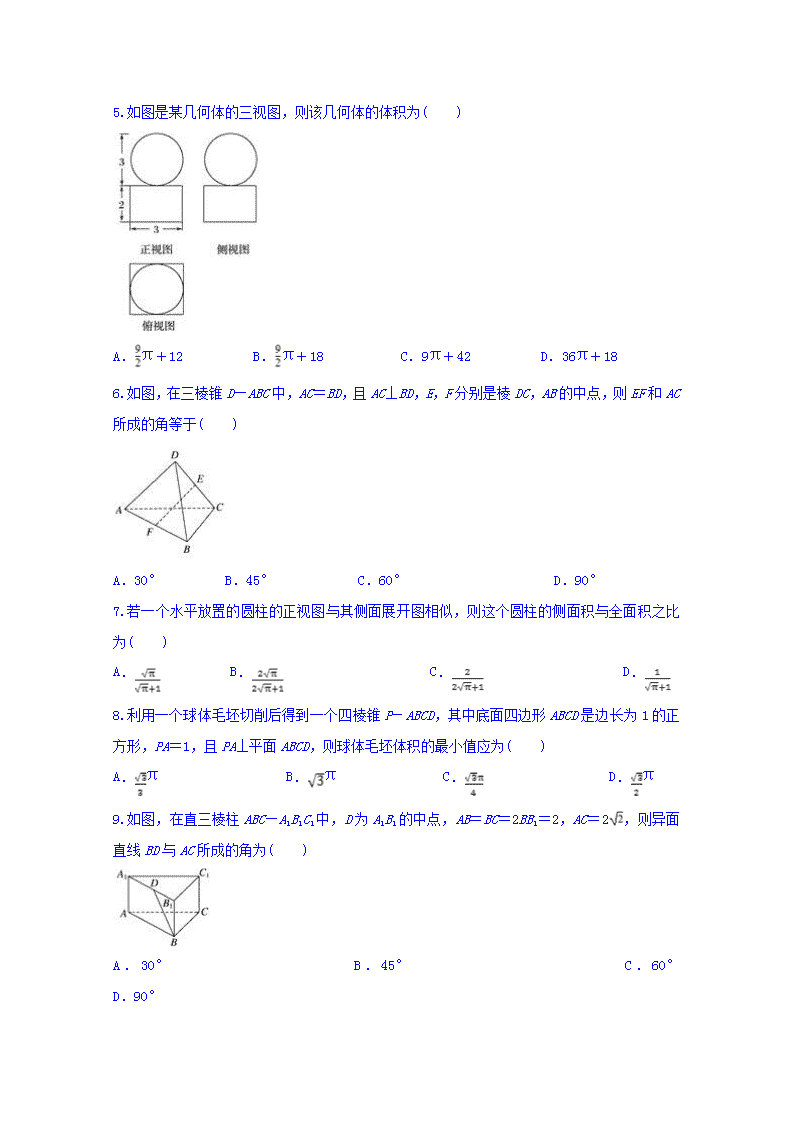
安徽省滁州市定远县民族中学2019-2020学年高二上学期期中考试数学（文）试题

定远县民族中学2019-2020学年上学期期中考试 高二文科数学试题 一、选择题(共12小题,每小题5分,共60分) ‎ ‎1.在空间中，α表示平面，m，n表示两条直线，则下列命题中错误的是(　　)‎ A．若m∥α，m，n不平行，则n与α不平行 B．若m∥α，m，n不垂直，则n与α不垂直 C．若m⊥α，m，n不平行，则n与α不垂直 D．若m⊥α，m，n不垂直，则n与α不平行 ‎2.一几何体的三视图如图所示，则该几何体的表面积为(　　)‎ A．20 B．‎24 C．16 D．16＋‎ ‎3.下列四个命题中正确命题的个数是(　　)‎ ‎①如果a，b是两条直线，a∥b，那么a平行于经过b的任何一个平面；‎ ‎②如果直线a和平面α满足a∥α，那么a与平面α内的任何一条直线平行；‎ ‎③如果直线a，b和平面α满足a∥b，a∥α，b⊄α，那么b∥α；‎ ‎④如果a与平面α上的无数条直线平行，那么直线a必平行于平面α.‎ A．0 B．1 C．2 D．3‎ ‎4.如图，四棱锥P－ABCD中，M，N分别为AC，PC上的点，且MN∥平面PAD，则(　　)‎ A．MN∥PD B．MN∥PA C．MN∥AD D．以上均有可能 ‎5.如图是某几何体的三视图，则该几何体的体积为(　　)‎ A．π＋12 B．π＋‎18 C．9π＋42 D．36π＋18‎ ‎6.如图，在三棱锥D—ABC中，AC＝BD，且AC⊥BD，E，F分别是棱DC，AB的中点，则EF和AC所成的角等于(　　)‎ A．30° B．45° C．60° D．90°‎ ‎7.若一个水平放置的圆柱的正视图与其侧面展开图相似，则这个圆柱的侧面积与全面积之比为(　　)‎ A． B． C． D．‎ ‎8.利用一个球体毛坯切削后得到一个四棱锥P－ABCD，其中底面四边形ABCD是边长为1的正方形，PA＝1，且PA⊥平面ABCD，则球体毛坯体积的最小值应为(　　)‎ A．π B．π C． D．π ‎9.如图，在直三棱柱ABC—A1B‎1C1中，D为A1B1的中点，AB＝BC＝2BB1＝2，AC＝2，则异面直线BD与AC所成的角为(　　)‎ A．30° B．45° C．60° D．90°‎ ‎10.已知在长方体中，底面是边长为2的正方形，高为4，则点到截面的距离是(　 　)‎ A. B. C. D. ‎ ‎11..设△ABC三边长为a， ， ；△ABC的面积为S，内切圆半径为，则，类比这个结论可知，四面体S-ABC的四个面的面积分别为，四面体S-ABC的体积为，内切球半径为，则=（ ）‎ A. B. ‎ C. D. ‎ ‎12.在四棱锥中，底面是一直角梯形，⊥，，，，⊥底面，是棱上异于，的动点，设，则“”是三棱锥的体积不小于1的（ ）‎ A．充分不必要条件 B．必要不充分条件 ‎ C．充要条件 D．既不充分也不必要条件 二、填空题(共4小题,每小题5分,共20分) ‎ ‎13.如图所示，ABCD—A1B‎1C1D1是棱长为a的正方体，M，N分别是下底面的棱A1B1，B‎1C1的中点，P是上底面的棱AD上的一点，AP＝，过P，M，N的平面交上底面于PQ，Q在CD上，则PQ＝________.‎ ‎14. 如图，已知正方体的棱长为，点是面的中心，点是面的对角线上一点，且平面，则线段的长为__________．‎ ‎15.如图是一个空间几何体的三视图，则该几何体的外接球的体积等于_________．‎ ‎16.三棱锥中， 分别为的中点，记三棱锥的体积为， 的体积为，则_________.‎ 三、解答题(共6小题,共70分) ‎ ‎17.（12分）如图所示，四边形ABCD是平行四边形，PB⊥平面ABCD，MA∥PB，PB＝2MA.‎ 在线段PB上是否存在一点F，使平面AFC∥平面PMD？若存在，请确定点F的位置；若不存在，请说明理由．‎ ‎18. （10分）如图，若△ABC所在的平面和△A1B‎1C1所在平面相交，并且直线AA1，BB1，CC1相交于一点O，求证：‎ ‎(1)AB和A1B1，BC和B‎1C1，AC和A‎1C1分别在同一平面内；‎ ‎(2)如果AB和A1B1，BC和B‎1C1， AC和A‎1C1分别相交，那么交点在同一直线上．‎ ‎19. （12分）如图，在三棱锥S－ABC中，SC⊥平面ABC，点P、M分别是SC和SB的中点，设PM＝AC＝1，∠ACB＝90°，直线AM与直线SC所成的角为60°.‎ ‎(1)求证：平面MAP⊥平面SAC；‎ ‎(2)求二面角M－AC－B的平面角的正切值．‎ ‎20. （12分）如图，已知AB是⊙O的直径，点C是⊙O上的动点(异于A、B)，过动点C的直线VC垂直于⊙O所在的平面，D，E分别是VA，VC的中点．‎ ‎(1)求证：直线ED⊥平面VBC；‎ ‎(2)若VC＝AB＝2BC，求直线EO与平面VBC所成角大小的正切值．‎ ‎21. （12分）已知，如图，平面PAB⊥平面ABC，平面PAC⊥平面ABC，AE⊥平面PBC，E为垂足．‎ ‎(1)求证：PA⊥平面ABC；‎ ‎(2)当E为△PBC的垂心时，求证：△ABC是直角三角形．‎ ‎22. （12分）如图，正方体的棱长为1，B′C∩BC′＝O，求：‎ ‎(1)AO与A′C′所成角的大小；‎ ‎(2)AO与平面ABCD所成角的正切值；‎ ‎(3)平面AOB与平面AOC所成角的大小．‎ 答案 ‎1.A 2.A 3.B 4.B 5.B 6.B 7.B 8.D 9.C 10.C 11.C 12.B ‎13.a ‎14. ．‎ ‎15.‎ ‎16.‎ ‎17.解　当点F是PB的中点时，平面AFC∥平面PMD，证明如下：如图连接AC和BD交于点O，连接FO，则PF＝PB.‎ ‎∵四边形ABCD是平行四边形，‎ ‎∴O是BD的中点，∴OF∥PD.‎ 又OF⊄平面PMD，PD⊂平面PMD，‎ ‎∴OF∥平面PMD.又MA∥PB且MA＝PB，‎ ‎∴PF∥MA且PF＝MA，‎ ‎∴四边形AFPM是平行四边形，‎ ‎∴AF∥PM.又AF⊄平面PMD，PM⊂平面PMD，‎ ‎∴AF∥平面PMD.‎ 又AF∩OF＝F，AF⊂平面AFC，OF⊂平面AFC，‎ ‎∴平面AFC∥平面PMD.‎ ‎18. 证明　(1)因为AA1∩BB1＝O，‎ 所以AA1，BB1确定平面ABO，‎ 所以A，A1，B，B1都在平面ABO内，‎ 所以AB⊂平面ABO，A1B1⊂平面ABO，即AB和A1B1在同一平面内．‎ 同理可证，BC和B‎1C1，AC和A‎1C1分别在同一平面内．‎ ‎(2)设AB∩A1B1＝P，‎ AC∩A‎1C1＝R，所以平面ABC∩平面A1B‎1C1＝PR.‎ 因为BC⊂平面ABC，B‎1C1⊂平面A1B‎1C1，‎ 且BC∩B‎1C1＝Q，‎ 所以Q∈PR，即P，R，Q在同一直线上．‎ ‎19.(1)证明　∵SC⊥平面ABC，∴SC⊥BC，‎ 又∵∠ACB＝90°，‎ ‎∴AC⊥BC，∵AC∩SC＝C，∴BC⊥平面SAC.‎ 又∵P，M是SC，SB的中点，‎ ‎∴PM∥BC，∴PM⊥平面SAC，‎ ‎∵PM⊂平面MAP，∴平面MAP⊥平面SAC.‎ ‎(2)解　∵AC⊥平面SBC，‎ ‎∴AC⊥CM，AC⊥CB，‎ 从而∠MCB为二面角M－AC－B的平面角．‎ ‎∵直线AM与直线PC所成的角为60°，‎ ‎∴过点M作MN⊥CB于N点，连接AN，‎ 则∠AMN＝60°，在△CAN中，‎ 由勾股定理得AN＝.‎ 在Rt△AMN中，MN＝＝·＝.‎ 在Rt△CNM中，tan∠MCN＝＝，‎ 故二面角M－AC－B的正切值为.‎ ‎20.(1)证明　如图，‎ ‎∵AB是⊙O的直径，∴AC⊥BC，‎ 又∵VC垂直于⊙O所在的平面，∴AC⊥VC，‎ 而BC∩VC＝C，∴AC⊥平面VBC.‎ 又∵D、E分别为VA、VC的中点，‎ ‎∴DE是△VCA的中位线，‎ ‎∴DE∥AC，∴DE⊥平面VBC.‎ ‎(2)解　设VC＝AB＝2BC＝‎2a，‎ 取BC的中点K，连接EK，OK，OC，‎ 在正△OBC中，OK＝a，且OK∥AC，‎ ‎∴OK⊥平面VBC，‎ ‎∴EK是斜线EO在平面VBC上的投影，‎ ‎∴∠OEK就是所求的线面角，‎ 而EK是Rt△VBC的中位线，‎ ‎∴EK＝a，‎ ‎∴tan∠OEK＝＝＝.‎ ‎21.证明　(1)在平面ABC内任取一点D，作DF⊥AC于点F，作DG⊥AB于点G.‎ ‎∵平面PAC⊥平面ABC，且交线为AC，‎ ‎∴DF⊥平面PAC.‎ ‎∵PA⊂平面PAC，∴DF⊥PA.‎ 同理可证DG⊥PA.‎ ‎∵DG∩DF＝D，∴PA⊥平面ABC.‎ ‎(2)连接BE并延长交PC于点H.‎ ‎∵E是△PBC的垂心，∴PC⊥BH.‎ 又∵AE是平面PBC的垂线，∴PC⊥AE.‎ ‎∵BH∩AE＝E，∴PC⊥平面ABE，∴PC⊥AB.‎ 又∵PA⊥平面ABC，∴PA⊥AB.‎ ‎∵PA∩PC＝P，∴AB⊥平面PAC，‎ ‎∴AB⊥AC，即△ABC是直角三角形．‎ ‎22. 解　(1)∵A′C′∥AC，‎ ‎∴AO与A′C′所成的角就是∠OAC.‎ ‎∵AB⊥平面BC′，OC⊂平面BC′，‎ ‎∴OC⊥AB，又OC⊥BO，AB∩BO＝B，AB，BO⊂平面ABO，‎ ‎∴OC⊥平面ABO.‎ 又OA⊂平面ABO，∴OC⊥OA.‎ 在Rt△AOC中，OC＝，AC＝，sin∠OAC＝＝，‎ ‎∴∠OAC＝30°.‎ 即AO与A′C′所成角为30°.‎ ‎(2)如图，作OE⊥BC于E，连接AE.‎ ‎∵平面BC′⊥平面ABCD，平面BC′∩平面ABCD＝BC，OE⊂平面BC′，‎ ‎∴OE⊥平面ABCD，‎ ‎∴∠OAE为OA与平面ABCD所成的角．‎ 在Rt△OAE中，OE＝，AE＝＝，‎ ‎∴tan∠OAE＝＝.‎ 即AO与平面ABCD所成角的正切值为.‎ ‎(3)由(1)可知OC⊥平面AOB.‎ 又∵OC⊂平面AOC，‎ ‎∴平面AOB⊥平面AOC.‎ 即平面AOB与平面AOC所成的角为90°.‎