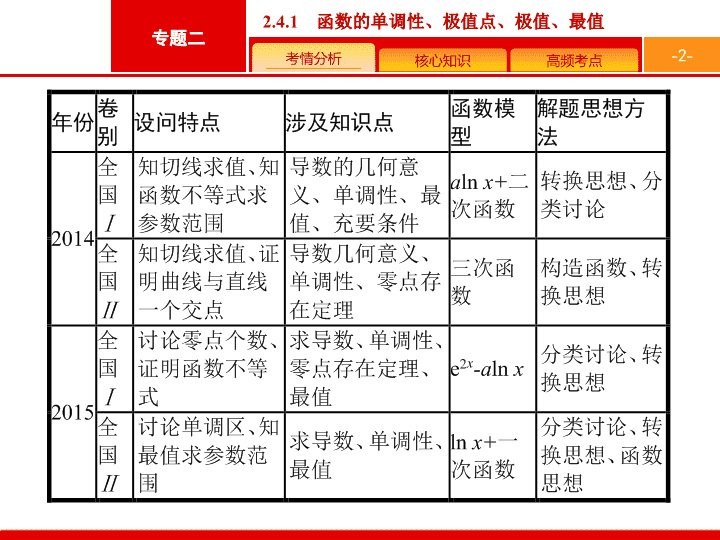
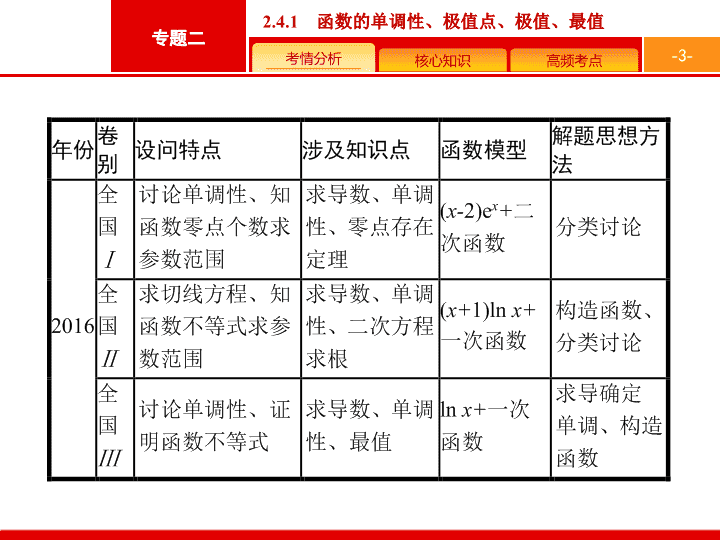
2019届二轮复习(文)2-2-4-1函数的单调性、极值点、极值、最值课件(37张)
2.4
[
压轴大题
1]
导数在函数中的应用
-
2
-
-
3
-
-
4
-
-
5
-
-
6
-
1
.
导数的几何意义
(1)
函数
f
(
x
)
在
x
0
处的导数是曲线
f
(
x
)
在点
P
(
x
0
,
f
(
x
0
))
处的切线的斜率
,
即
k=f'
(
x
0
)
.
(2)
函数切线问题的求解策略
:
用好切点
“
三重性
”:
①
切点在函数图象上
,
满足函数解析式
;
②
切点在切线上
,
满足切线方程
;
③
切点处的导数等于切线的斜率
.
2
.
函数的导数与单调性的关系
函数
y=f
(
x
)
在
(
a
,
b
)
内可导
,
(1)
若
f'
(
x
)
>
0
在
(
a
,
b
)
内恒成立
,
则
f
(
x
)
在
(
a
,
b
)
内单调递增
;
(2)
若
f'
(
x
)
<
0
在
(
a
,
b
)
内恒成立
,
则
f
(
x
)
在
(
a
,
b
)
内单调递减
.
-
7
-
3
.
函数的导数与单调性的等价关系
函数
f
(
x
)
在
(
a
,
b
)
内可导
,
f'
(
x
)
在
(
a
,
b
)
任意子区间内都不恒等于
0
.f'
(
x
)
≥
0
⇔
f
(
x
)
在
(
a
,
b
)
上为增函数
.f'
(
x
)
≤
0
⇔
f
(
x
)
在
(
a
,
b
)
上为减函数
.
4
.
函数的极值、最值
(1)
若在
x
0
附近左侧
f'
(
x
)
>
0,
右侧
f'
(
x
)
<
0,
则
f
(
x
0
)
为函数
f
(
x
)
的极大值
;
若在
x
0
附近左侧
f'
(
x
)
<
0,
右侧
f'
(
x
)
>
0,
则
f
(
x
0
)
为函数
f
(
x
)
的极小值
.
(2)
设函数
y=f
(
x
)
在
[
a
,
b
]
上连续
,
在
(
a
,
b
)
内可导
,
则
f
(
x
)
在
[
a
,
b
]
上必有最大值和最小值且在极值点或端点处取得
.
(3)
若函数
f
(
x
)
在
[
a
,
b
]
上单调递增
,
则
f
(
a
)
为函数的最小值
,
f
(
b
)
为函数的最大值
;
若函数
f
(
x
)
在
[
a
,
b
]
上单调递减
,
则
f
(
a
)
为函数的最大值
,
f
(
b
)
为函数的最小值
.
-
8
-
5
.
常见恒成立不等式
(1)ln
x
≤
x-
1;(2)e
x
≥
x+
1
.
6
.
构造辅助函数的四种方法
(1)
移项法
:
证明不等式
f
(
x
)
>g
(
x
)(
f
(
x
)
0(
f
(
x
)
-g
(
x
)
<
0),
进而构造辅助函数
h
(
x
)
=f
(
x
)
-g
(
x
);
(2)
构造
“
形似
”
函数
:
对原不等式同解变形
,
如移项、通分、取对数
;
把不等式转化为左右两边是相同结构的式子的结构
,
根据
“
相同结构
”
构造辅助函数
;
(3)
主元法
:
对于
(
或可化为
)
f
(
x
1
,
x
2
)
≥
A
的不等式
,
可选
x
1
(
或
x
2
)
为主元
,
构造函数
f
(
x
,
x
2
)(
或
f
(
x
1
,
x
));
(4)
放缩法
:
若所构造函数最值不易求解
,
可将所证明不等式进行放缩
,
再重新构造函数
.
-
9
-
7
.
函数不等式的类型与解法
(1)
∀
x
∈
D
,
f
(
x
)
≤
k
⇔
f
(
x
)
max
≤
k
;
∃
x
∈
D
,
f
(
x
)
≤
k
⇔
f
(
x
)
min
≤
k
;
(2)
∀
x
∈
D
,
f
(
x
)
g
(
x
2
)
⇔
f
(
x
)
在
[
a
,
b
]
上的最小值
>g
(
x
)
在
[
c
,
d
]
上的最大值
.
(2)
∃
x
1
∈
[
a
,
b
],
x
2
∈
[
c
,
d
],
f
(
x
1
)
>g
(
x
2
)
⇔
f
(
x
)
在
[
a
,
b
]
上的最大值
>g
(
x
)
在
[
c
,
d
]
上的最小值
.
(3)
∀
x
1
∈
[
a
,
b
],
∃
x
2
∈
[
c
,
d
],
f
(
x
1
)
>g
(
x
2
)
⇔
f
(
x
)
在
[
a
,
b
]
上的最小值
>g
(
x
)
在
[
c
,
d
]
上的最小值
.
-
10
-
(4)
∃
x
1
∈
[
a
,
b
],
∀
x
2
∈
[
c
,
d
],
f
(
x
1
)
>g
(
x
2
)
⇔
f
(
x
)
在
[
a
,
b
]
上的最大值
>g
(
x
)
在
[
c
,
d
]
上的最大值
.
(5)
∃
x
1
∈
[
a
,
b
],
当
x
2
∈
[
c
,
d
]
时
,
f
(
x
1
)
=g
(
x
2
)
⇔
f
(
x
)
在
[
a
,
b
]
上的值域与
g
(
x
)
在
[
c
,
d
]
上的值域交集非空
.
(6)
∀
x
1
∈
[
a
,
b
],
∃
x
2
∈
[
c
,
d
],
f
(
x
1
)
=g
(
x
2
)
⇔
f
(
x
)
在
[
a
,
b
]
上的值域
⊆
g
(
x
)
在
[
c
,
d
]
上的值域
.
(7)
∀
x
2
∈
[
c
,
d
],
∃
x
1
∈
[
a
,
b
],
f
(
x
1
)
=g
(
x
2
)
⇔
f
(
x
)
在
[
a
,
b
]
上的值域
⊇
g
(
x
)
在
[
c
,
d
]
上的值域
.
-
11
-
9
.
求解导数应用题宏观上的解题思想是
借助导函数
(
正负
)
研究原函数
(
单调性
);
重点是把导函数先
“
弄熟悉
”;
为了把导函数先
“
弄熟悉
”
采取的措施
:
(1)
通分
;
(2)
二次求导或三次求导
;
(3)
能画出导函数草图是最好的
!
2.4.1
函数的单调性、极值点
、
极值
、最值
-
13
-
考向一
考向二
考向三
考向四
求单调区间或讨论单调性
(
多维探究
)
例
1
(2018
江西南昌一模
,
文
21
节选
)
已知函数
f
(
x
)
=
e
x
-a
ln
x-
e(
a
∈
R
),
其中
e
为自然对数的底数
.
(1)
若
f
(
x
)
在
x=
1
处取到极小值
,
求
a
的值及函数
f
(
x
)
的单调区间
;
(2)
略
.
-
14
-
考向一
考向二
考向三
考向四
-
15
-
考向一
考向二
考向三
考向四
解题心得
求
f
(
x
)
的单调区间
,
需知
f'
(
x
)
的正负
,
若
f'
(
x
)
不含参数
,
但又不好判断正负
,
将
f'
(
x
)
中正负不定的部分设为
g
(
x
),
对
g
(
x
)
再进行一次或二次求导
,
由
g'
(
x
)
的正负及
g
(
x
)
的零点判断出
g
(
x
)
的正负
,
进而得出
f'
(
x
)
的正负
.
-
16
-
考向一
考向二
考向三
考向四
对点训练
1
(2018
青海西宁一模
,
文
21
节选
)
设
f
(
x
)
=
ln
x
,
g
(
x
)
= x|x
|.
(1)
令
F
(
x
)
=xf
(
x
)
-g
(
x
),
求
F
(
x
)
的单调区间
;
(2)
略
.
-
17
-
考向一
考向二
考向三
考向四
-
18
-
考向一
考向二
考向三
考向四
例
2
(2018
福建龙岩
4
月质检
,
文
21
节选
)
已知
函数
m
∈
R
.
(1)
求函数
f
(
x
)
的单调增区间
;
(2)
略
.
-
19
-
考向一
考向二
考向三
考向四
当
-
1
0,
f'
(
x
)
>
0;
在
(
x
1
,
x
2
)
上
,
g
(
x
)
<
0,
f'
(
x
)
<
0
.
所以函数
f
(
x
)
在
(0,
x
1
),(
x
2
,
+∞
)
上单调递增
,
在
(
x
1
,
x
2
)
上单调递减
.
当
m
≥
0,
即
x
1
<
0
0,
f'
(
x
)
>
0
.
所以函数
f
(
x
)
在
(0,
x
2
)
上单调递减
,
在
(
x
2
,
+∞
)
上单调递增
.
综上
,
当
m
≤
-
1
时
,
函数
f
(
x
)
在
(0,
+∞
)
上单调递增
;
-
20
-
考向一
考向二
考向三
考向四
解题心得
在求函数
f
(
x
)
的单调区间时
,
若
f'
(
x
)
中含有参数不容易判断其正负时
,
需要对参数进行分类
,
本例分类的标准
(1)
按导函数是否有零点分大类
;(2)
在小类中再按导函数零点的大小比较分小类
;(3)
在小类中再按零点是否在定义域中分类
.
-
21
-
考向一
考向二
考向三
考向四
对点训练
2
已知函数
f
(
x
)
=
ln
x-mx
(
m
∈
R
)
.
(1)
若
m=
1,
求曲线
y=f
(
x
)
在点
P
(1,
-
1)
处的切线方程
;
(2)
讨论函数
f
(
x
)
在
(1,e)
上的单调性
.
-
22
-
考向一
考向二
考向三
考向四
-
23
-
考向一
考向二
考向三
考向四
讨论函数极值点的个数
例
3
(
节选
)
设函数
f
(
x
)
=
ln(
x+
1)
+a
(
x
2
-x
),
其中
a
∈
R
.
(1)
讨论函数
f
(
x
)
极值点的个数
,
并说明理由
;
(2)
略
.
解
:
(1)
定义域为
(
-
1,
+∞
),
令
g
(
x
)
=
2
ax
2
+ax+
1
-a
(
x>-
1),
当
a=
0
时
,
g
(
x
)
=
1,
则
f'
(
x
)
>
0
在
(
-
1,
+∞
)
上恒成立
,
则
f
(
x
)
在
(
-
1,
+∞
)
上单调递增
,
即当
a=
0
时
,
函数无极值点
;
-
24
-
考向一
考向二
考向三
考向四
-
25
-
考向一
考向二
考向三
考向四
-
26
-
考向一
考向二
考向三
考向四
解题心得
利用导数求含参数的原函数的单调区间
→
极值
→
最值
→
恒成立问题的步骤
:
1
.
求函数定义域
;
2
.
求导
→
通分或因式分解或二次求导
(
目的
:
把导函数
“
弄熟悉
”);
3
.
对参数分类
,
分类的层次
:(1)
按导函数的类型分大类
;
(2)
按导函数是否有零点分小类
;
(3)
在小类中再按导函数零点的大小分小类
;
(4)
在小类的小类中再按零点是否在定义域中分小类
.
-
27
-
考向一
考向二
考向三
考向四
对点训练
3
(2018
湖南衡阳一模
,
理
21
节选
)
已知函数
f
(
x
)
=
ln
x+x
2
-ax
(
a>
0)
.
(1)
讨论
f
(
x
)
在
(0,1)
上的极值点的个数
;
(2)
略
.
-
28
-
考向一
考向二
考向三
考向四
-
29
-
考向一
考向二
考向三
考向四
求函数的极值、最值
例
4
(2018
宁夏银川一中一模
,
理
21)
已知函数
f
(
x
)
=
ln
x-ax
2
+
(
a-
2)
x.
(1)
若
f
(
x
)
在
x=
1
处取得极值
,
求
a
的值
;
(2)
求函数
y=f
(
x
)
在
[
a
2
,
a
]
上的最大值
.
-
30
-
考向一
考向二
考向三
考向四
-
31
-
考向一
考向二
考向三
考向四
解题心得
求最值的常用方法是由导数确定单调性
,
由单调性确定极值
,
比较极值与定义域的端点值确定最值
.
-
32
-
考向一
考向二
考向三
考向四
对点训练
4
已知函数
f
(
x
)
=
ln
x- ax
2
+x
,
a
∈
R
.
(1)
当
a=
0
时
,
求函数
f
(
x
)
在
(1,
f
(1))
处的切线方程
;
(2)
令
g
(
x
)
=f
(
x
)
-ax+
1,
求函数
g
(
x
)
的极值
.
-
33
-
考向一
考向二
考向三
考向四
-
34
-
考向一
考向二
考向三
考向四
在恒成立中求参数的极值、最
值
例
5
(2018
陕西榆林一模
,
文
21)
已知函数
f
(
x
)
=
e
x
-a
(
x-
1),
其中
a>
0,e
为自然对数的底数
.
(1)
求函数
f
(
x
)
的单调区间
;
(2)
已知
b
∈
R
,
若函数
f
(
x
)
≥
b
对任意
x
∈
R
都成立
,
求
ab
的最大值
.
解
(1)
因为
f'
(
x
)
=
e
x
-a
,
当
a>
0
时
,
由
f'
(
x
)
=
0
得
x=
ln
a
,
所以当
x
∈
(
-∞
,ln
a
)
时
,
f'
(
x
)
<
0,
f
(
x
)
单调递减
;
当
x
∈
(ln
a
,
+∞
)
时
,
f'
(
x
)
>
0,
f
(
x
)
单调递增
.
综上
,
当
a>
0
时
,
函数
f
(
x
)
的单调递增区间为
(ln
a
,
+∞
),
单调递减区间为
(
-∞
,ln
a
)
.
-
35
-
考向一
考向二
考向三
考向四
(2)
当
a>
0
时
,
由函数
f
(
x
)
≥
b
对任意
x
∈
R
都成立
,
得
b
≤
f
(
x
)
min
,
因为
f
(
x
)
min
=f
(ln
a
)
=
2
a-a
ln
a
,
所以
b
≤
2
a-
ln
a.
所以
ab
≤
2
a
2
-a
2
ln
a
,
设
g
(
a
)
=
2
a
2
-a
2
ln
a
(
a>
0),
所以
g'
(
a
)
=
4
a-
(2
a
ln
a+a
)
=
3
a-
2
a
ln
a
,
-
36
-
考向一
考向二
考向三
考向四
解题心得
1
.k
≤
f
(
x
)(
或
k
≥
f
(
x
))
恒成立
,
求参数
k
的最值问题
,
一般的解题思路是
,
先求
f
(
x
)
的最小值
(
或最大值
),
得出关于
k
≤
g
(
t
)(
或
k
≥
g
(
t
))
的函数不等式
,
然后再求函数
g
(
t
)
的最值
.
从而得出
k
的最值
.
2
.
对于导函数的零点存在但不可求的问题
,
可根据零点存在定理确定出零点所在的区间
,
在求函数的最值时可利用整体代换的方法求解
,
这是在用导数解决函数问题中常见的一种类型
.
-
37
-
考向一
考向二
考向三
考向四
对点训练
5
(2018
宁夏银川一中一模
,
文
21)
已知函数
f
(
x
)
=ax
3
-x
2
+bx
(
a
,
b
∈
R
),
f'
(
x
)
为其导函数
,
且
x=
3
时
f
(
x
)
有极小值
-
9
.
(1)
求
f
(
x
)
的单调递减区间
;
(2)
若不等式
f'
(
x
)
>k
(
x
ln
x-
1)
-
6
x-
4(
k
为正整数
)
对任意正实数
x
恒成立
,
求
k
的最大值
.
(
解答过程可参考使用以下数据
:ln 7≈1
.
95,ln 8≈2
.
08)