2020年高考数学(理)二轮复习讲练测 专题23 立体几何角的计算问题（练）（原卷版）

2020年高考数学(理)二轮复习讲练测 专题23 立体几何角的计算问题（练）（原卷版）

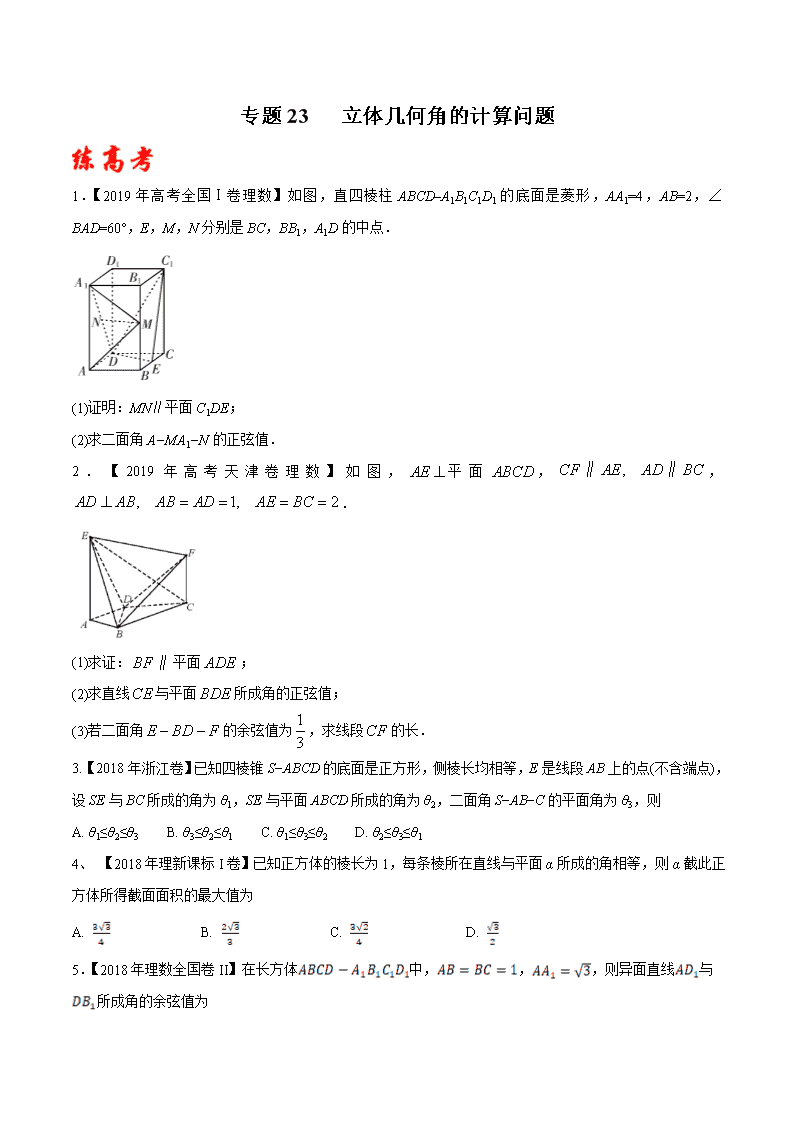
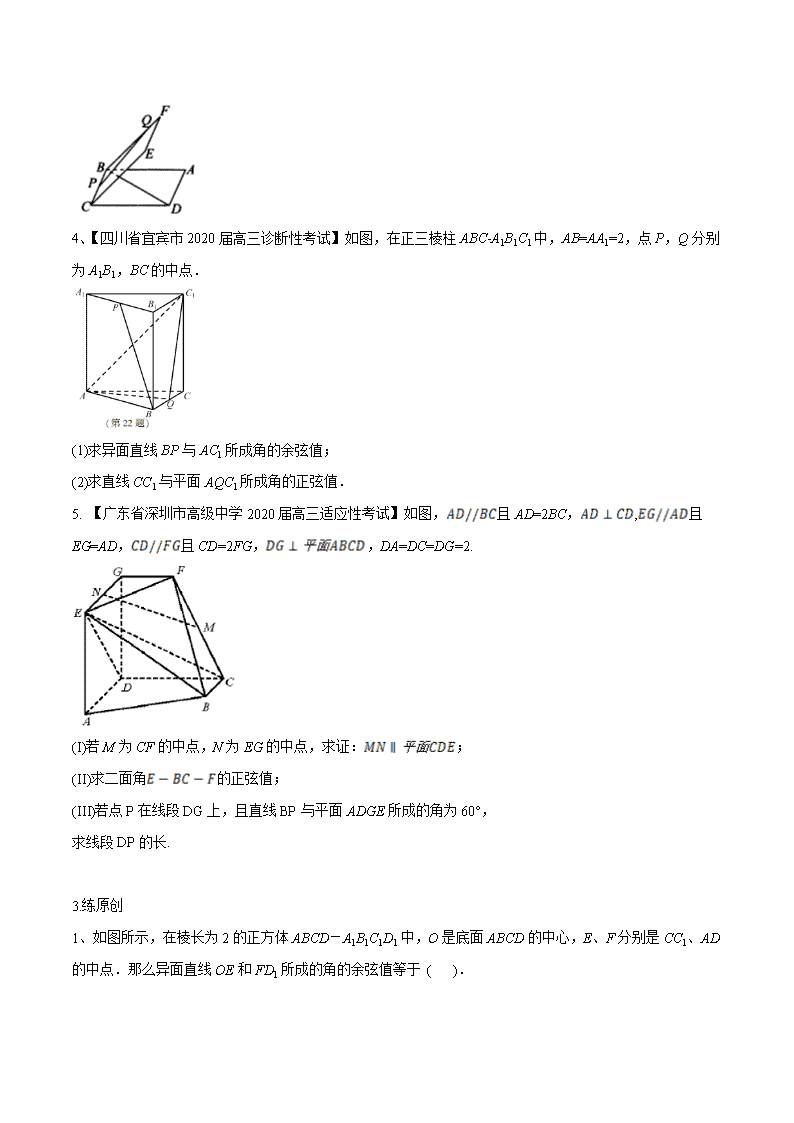
专题23 立体几何角的计算问题 ‎1．【2019年高考全国Ⅰ卷理数】如图，直四棱柱ABCD–A1B1C1D1的底面是菱形，AA1=4，AB=2，∠BAD=60°，E，M，N分别是BC，BB1，A1D的中点．‎ ‎(1)证明：MN∥平面C1DE；‎ ‎(2)求二面角A−MA1−N的正弦值．‎ ‎2．【2019年高考天津卷理数】如图，平面，，．‎ ‎(1)求证：平面；‎ ‎(2)求直线与平面所成角的正弦值；‎ ‎(3)若二面角的余弦值为，求线段的长．‎ ‎3.【2018年浙江卷】已知四棱锥S−ABCD的底面是正方形，侧棱长均相等，E是线段AB上的点(不含端点)，设SE与BC所成的角为θ1，SE与平面ABCD所成的角为θ2，二面角S−AB−C的平面角为θ3，则 A. θ1≤θ2≤θ3 B. θ3≤θ2≤θ1 C. θ1≤θ3≤θ2 D. θ2≤θ3≤θ1‎ ‎4、 【2018年理新课标I卷】已知正方体的棱长为1，每条棱所在直线与平面α所成的角相等，则α截此正方体所得截面面积的最大值为 A. B. C. D. ‎ ‎5．【2018年理数全国卷II】在长方体中，，，则异面直线与所成角的余弦值为 A. B. C. D. ‎ ‎2.练模拟 ‎1. (2019·四川双流中学高一月考)如图，在底面为正方形，侧棱垂直于底面的四棱柱中，，则异面直线，所成的角的余弦值为( ) ‎ A． B． ‎ C． D．‎ ‎2. 【陕西省2019届高三年级第三次联考数学试题】已知三棱柱的侧棱与底面边长都相等，在底面上的射影为的中点，则异面直线与所成的角的余弦值为 A． B．‎ C． D．‎ ‎3.【河北省衡水金卷2019年调研卷】如图，将正方形沿着边抬起到一定位置得到正方形，并使得平面与平面所成的二面角为，为正方形内一条直线，则直线与所成角的取值范围为_______. ‎ ‎4、【四川省宜宾市2020届高三诊断性考试】如图，在正三棱柱ABC-A1B1C1中，AB=AA1=2，点P，Q分别为A1B1，BC的中点．‎ ‎(1)求异面直线BP与AC1所成角的余弦值；‎ ‎(2)求直线CC1与平面AQC1所成角的正弦值．‎ ‎5. 【广东省深圳市高级中学2020届高三适应性考试】如图，且AD=2BC，,且EG=AD，且CD=2FG，，DA=DC=DG=2. ‎ ‎(I)若M为CF的中点，N为EG的中点，求证：；‎ ‎(II)求二面角的正弦值；‎ ‎(III)若点P在线段DG上，且直线BP与平面ADGE所成的角为60°，‎ 求线段DP的长.‎ ‎3.练原创 ‎1、如图所示，在棱长为2的正方体ABCD－A1B1C1D1中，O是底面ABCD的中心，E、F分别是CC1、AD的中点．那么异面直线OE和FD1所成的角的余弦值等于 ( )．‎ A． B． C． D．‎ ‎2．若直线的方向向量，平面的一个法向量，则直线与平面所成角的正弦值等于___．‎ ‎3、在三棱锥中，，且，，两两垂直，点为的中点，则直线与平面所成的角的正弦值是__________．‎ ‎4. 如图，已知正三棱柱的所有棱长均为2，则直线与平面所成角的正弦值为________.‎ ‎5.如图，已知△中，∠=90°，，且=1，=2，△绕旋转至，使点与点之间的距离=．‎ ‎(1)求证：⊥平面；(2)求二面角的大小；‎ ‎(3)求异面直线与所成的角的余弦值．‎