- 2021-06-23 发布 |
- 37.5 KB |
- 8页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2017-2018学年福建省泉州市泉港区第一中学高二下学期第一次月考试题(4月) 数学(文) Word版
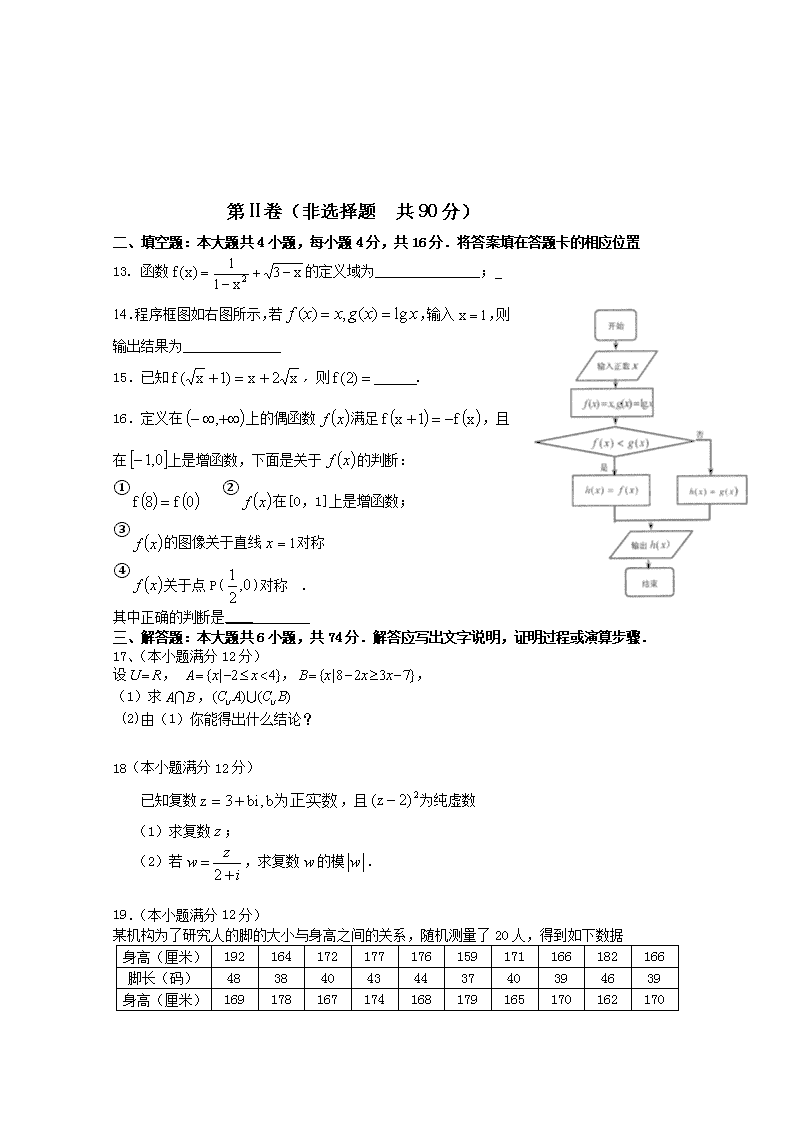
泉港一中2017-2018学年下学期第一次月考 高二数学(文科) 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题).本试卷共6页,满分150分.考试时间120分钟. 第Ⅰ卷(选择题 共60分) 一、 选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1. 设集合,,,则图中阴影( )部分所表示的集合是 A. B. C. D. 2. 在复平面内,复数对应的点位于( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 3.下列说法正确的是( ) A.命题“,均有”的否定是:“,使”; B.“”是“”的必要不充分条件; C. 命题“若,则”的逆否命题是真命题 ; D. 若命题为真则命题一定为真 4.用反证法证明命题“三角形中最多只有一个内角是钝角”时,结论的否定是( ) A.没有一个内角是钝角 B.有两个内角是钝角 C.至少有两个内角是钝角 D.有三个内角是钝角 5. 下列函数中,在其定义域内既是奇函数,又是增函数函数的是( ) A. B. C. D. 6. 年劳动生产率(千元)和工人工资(元)之间回归方程为,这意味着年劳动生产率每提高1千元时,工人工资平均( ) A.增加10元 B.减少10元 C.增加80元 D.减少80元 7、演绎推理“因为指数函数()是增函数,而函数 是指数函数,所以是增函数”所得结论错误的原因是( ) A.大前提错误 B.小前提错误 C.推理过程错误 D.以上都不是 8.甲、乙、丙、丁四位同学各自对A,B两变量的线性相关性做试验,并由回归分析法分别求得相关指数R与残差平方和m如下表: 甲 乙 丙 丁 R 0.85 0.78 0.69 0.82 m 103 106 124 115 则哪位同学的试验结果体现A,B两变量更强的线性相关性( ) A.甲 B.乙 C.丙 D.丁 9. 已知使成立的x 取值范围是( ) A.[-4,2) B.[-4,2] C.(0,2] D.(-4,2] 10.下面给出了关于复数的四种类比推理: ①若a,b∈R,则a-b>0a>b”类比推出“若a,b∈C,则a-b>0a>b”; ②复数的加减法运算可以类比多项式的加减法运算法则 ③ 由实数a绝对值的性质|a|2=a2类比得到复数z的性质|z|2=z2; ④由向量加法的几何意义可以类比得到复数加法的几何意义. 其中类比得到的结论错误的是( ). A.①③ B.②④ C.②③ D.①④ 11.已知函数是偶函数,在内单调递减,则实数=( ) A. B. C. D. 12. 四个小动物换座位,开始是鼠、猴、兔、猫分别坐在1,2,3,4号位子上(如图),第一次前后排动物互换座位,第二次左右列动物互换座位,…,这样交替进行下去,那么第2 015 次互换座位后,小兔的座位对应的是( ). A.编号1 B.编号2 C.编号3 D.编号4 第Ⅱ卷(非选择题 共90分) 二、填空题:本大题共4小题,每小题4分,共16分.将答案填在答题卡的相应位置 13. 函数的定义域为_______________; 14.程序框图如右图所示,若,输入,则输出结果为______________ 15.已知,则 . 16.定义在上的偶函数满足,且在上是增函数,下面是关于的判断: ① ②在[0,1]上是增函数; ③的图像关于直线对称 ④关于点P()对称 . 其中正确的判断是____ 三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤. 17、(本小题满分12分) 设, ,, (1)求, (2)由(1)你能得出什么结论? 18(本小题满分12分) 已知复数,且为纯虚数 (1)求复数; (2)若,求复数的模. 19.(本小题满分12分) 某机构为了研究人的脚的大小与身高之间的关系,随机测量了20人,得到如下数据 身高(厘米) 192 164 172 177 176 159 171 166 182 166 脚长(码) 48 38 40 43 44 37 40 39 46 39 身高(厘米) 169 178 167 174 168 179 165 170 162 170 脚长(码) 43 41 40 43 40 44 38 42 39 41 (1)若“身高大于175厘米”的为“高个”,“身高小于等于175厘米”的为“非高个”;“脚长大于42码”的为“大脚”,“脚长小于等于42码”的为“非大脚”,请根据上表数据完成下面的2×2列联表。 (2)根据(1)中的2×2列联表,试运用独立性检验的思想方法:能否在犯错误的概率不超过0.01的前提下认为脚的大小与身高之间有关系。 高个 非高个 合计 大脚 非大脚 12 合计 20 参考公式:,其中 参考数据: P(k2>k) 0.50 0.40 0.25 0.15 0.10 0.05 0.025 0.010 0.005 0.001 k 0.455 0.708 1.323 2.072 2.706 3.84 5.024 6.635 7.879 10.83 20.(本小题满分12分)已知二次函数的图象经(0,0),(1,2),(-1,-4)三点, (1)求该二次函数的解析式和最值; (2)已知函数在(t-1,+∞)上为减函数,求实数t的取值范围. 21.(本小题满分12分)已知定义在区间上的函数为奇函数。 (1)求函数的解析式并判断函数上的单调性 (2)解关于的不等式. 22(本小题满分14分)已知函数, (1)判断函数的奇偶性并求当时函数的单调区间; (2)若关于的方程有实数解,求实数的取值范围. 2017-2018学年下学期第一次月考 高二数学(文科)参考答案 一、选择题 题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 B C D C D C A A B A B D 二 填空题13. 14. 15. 3 16. ①③④ 三 解答题 17. 【解析】 解:(1)∵A=,B={x|x≤3};= CRA={x| x<-2或x≥4} CRB={x| x>3} ={x| x<-2或x>3}………8分 (2) …………12分 18 【解析】 解:(1) ∴,.又b为正实数 ∴b=1.∴z=3+i. , ………………………………6分 (2) ………………7分 ………………… 12分 19. 解: (1) 高个 非高个 合计 大脚 5 2 7 非大脚 1 12 13 合计 6 14 20 …6分 (2)假设成立:脚的大小与身高之间没有关系 K2的观测值 …………………………………8分 ∵,又8.802 6.635 ∴在犯错误的概率不超过0.01的前提下可以认为脚的大小与身高之间有关系.…………………………12分 20.【解析】设这个二次函数的解析式是y=ax+bx+c(a≠0),把(0,0),(1,1),(-1,-4)代入得: c=0 a+b+c=1 a−b+c=−3 , 解之得 a=−1 b=2 c=0 ; 所以该函数的解析式为:y=-x+2x. 因为, 当x=1时函数值最大值为1,无最小值;[]………………………………8分 (2)∵函数f(x)在(t-1,+∞)上是减的,∴t-1≥1.∴t≥2. …………… 12分 21.【解析】(1)是在区间上的奇函数 ……………………2分 设 则 即 函数在区间上是增函数 …………………6分 证法二:用导数证明 (2),且为奇函数 又函数在区间上是增函数,解得 故关于的不等式的解集为 …………………12分 22. 解:.解:(1)函数的定义域为{且} ∴为偶函数 当时, 若,则,递减; 若, 则,递增. 得的递增区间是;递减区间是. 查看更多