数学文卷·2017届山东省潍坊实验中学高三上学期第三次检测（2016

数学文卷·2017届山东省潍坊实验中学高三上学期第三次检测（2016

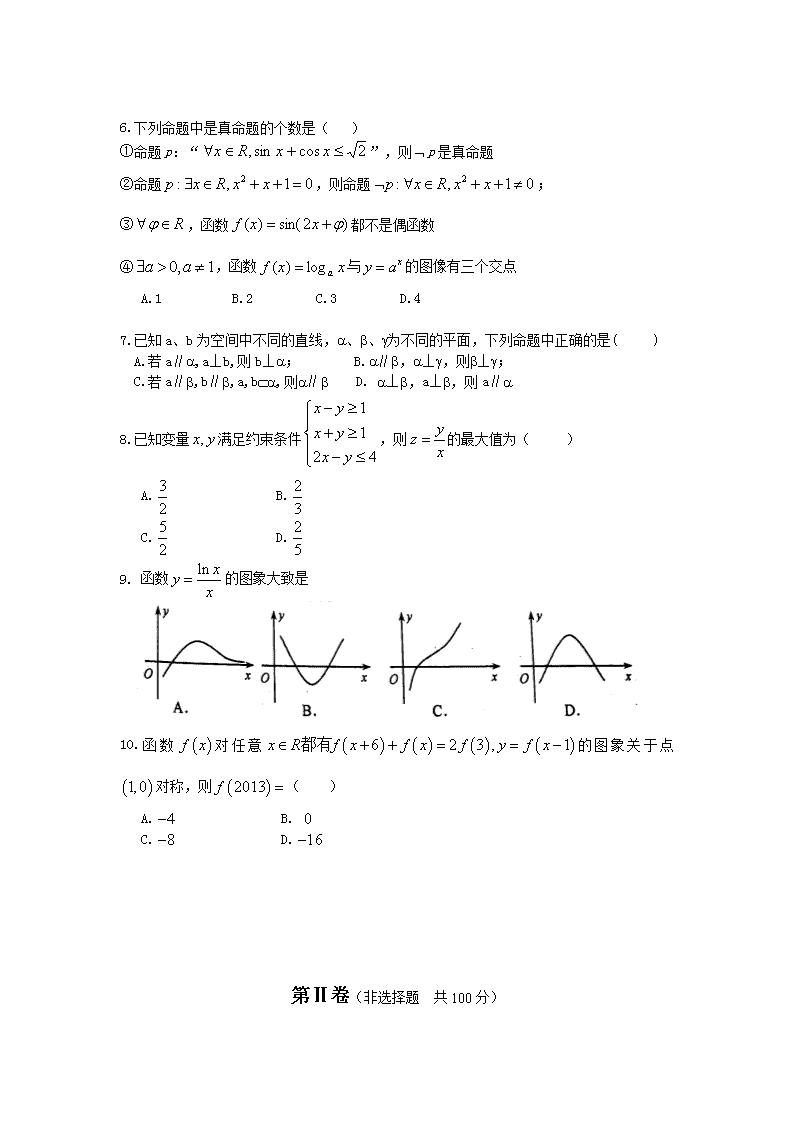
保密 启用前 试卷类型：A ‎2016-2017上学期高三年级单元过关检测三 数学（文）试题 本试卷共4页，分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分，考试时间120分钟.‎ 第Ⅰ卷（选择题 共50分）‎ 注意事项：‎ 1. 答第Ⅰ卷前，考生务必将自己的姓名、准考证号、考试科目用铅笔涂写在答题卡上.‎ ‎2.每题选出答案后，用2B铅笔把答题卡对应题目的答案标号涂黑.如需改动，用橡皮擦干净后，再改涂其它答案标号. ‎ 一、选择题（本题共10小题，每小题5分，共50分。在每小题给出的四个选项中，只有一项是符合题目要求的）‎ ‎1.已知全集集合则（ ）‎ A. B. C. D.‎ ‎2.设,且,则(　　)‎ A. B. C. D.‎ ‎3.已知，则（ ）‎ A. B. C. D. ‎ ‎4. 某工厂对一批产品进行了抽样检测，右图是根据抽样检测后的产品净重（单位：克）数据绘制的频率分散直方图，其中产品净重的范围是，样本数据分组为.已知样本中产品净重小于‎100克的个数是36，则样本中净重大于或等于‎98克并且小于‎102克的产品的个数是 A.90 B‎.75 ‎ C.60 D.45 ‎ ‎5.已知函数 ，则 的值是（ ）‎ A.9 B. C.－9 D.－‎ ‎6.下列命题中是真命题的个数是（ ）‎ ‎①命题p：“”，则p是真命题 ‎②命题，则命题；‎ ‎③，函数都不是偶函数 ‎④，函数与的图像有三个交点 A.1 B‎.2 ‎ C.3 D.4‎ ‎7.已知a、b为空间中不同的直线，a、b、g为不同的平面，下列命题中正确的是( )‎ A.若a∥a,a⊥b,则b⊥a； B.a∥b，a⊥g，则b⊥g；‎ C.若a∥b,b∥b,a,bÌa,则a∥b D. a⊥b，a⊥b，则a∥a ‎8.已知变量满足约束条件，则的最大值为（ ） ‎ A. B. ‎ ‎ C. D.‎ ‎9. 函数的图象大致是 ‎10.函数对任意的图象关于点对称，则（ ）‎ A. B. ‎ ‎ C. D.‎ 第Ⅱ卷（非选择题 共100分）‎ 注意事项：‎ 1. 将第Ⅱ卷答案用‎0.5mm的黑色签字笔答在答题纸的相应位置上.‎ ‎2.答卷前将密封线内的项目填写清楚.‎ 二、填空题：本大题共5小题，每小题5分，共25分。‎ ‎11.等比数列中，已知，则的值为 .‎ ‎12. 一个四面体的三视图如图所示，则该四面体的表面积是 。‎ ‎13. 在△ABC中，角A,B,C所对的边分别为a，b，c，已知的面积为__________.‎ ‎14.若直线平分圆，则的最小值是 . ‎ ‎15. 已知F是双曲线C：x2－my2＝‎3m(m>0)的一个焦点，则点F到C的一条渐近线的距离为 .‎ 三、解答题：本大题共6小题，共75分。解答应写出文字说明，证明过程或演算步骤。‎ ‎16. 某校从参加市联考的甲、乙两班数学成绩110分以上的同学中各随机抽取8人，将这16人的数学成绩编成茎叶图，如图所示.‎ ‎（I）茎叶图中有一个数据污损不清（用△表示），若甲班抽出来的同学平均成绩为122分，试推算这个污损的数据是多少？‎ ‎（II）现要从成绩在130分以上的5位同学中选2位作数学学习方法介绍，请将所有可能的结果列举出来，并求选出的两位同学不在同一个班的概率.‎ ‎17.已知向量＝(a,b)，＝(sin2x,2cos2x)，若f(x)＝.,且 ‎⑴ 求的值；‎ ‎⑵ 求函数在的最值及取得最值时的的集合；‎ ‎18.如图，矩形中，分别在线段上，，将矩形沿折起，记折起后的矩形为，且平面.‎ ‎⑴ 求证：；⑵ 若，求证：；‎ ‎19.设数列的前项和为，且。数列满足 ‎⑴ 求数列的通项公式；‎ ‎⑵ 证明：数列为等差数列，并求的前n项和Tn；‎ ‎20.已知函数.‎ ‎（1）若在定义域上为增函数，求实数a的取值范围；‎ ‎（2）若，求函数在区间上的最小值.‎ ‎21.设椭圆过点分别为椭圆C的左、右两个焦点，且离心率 ‎（1）求椭圆C的方程；‎ ‎（2）已知A为椭圆C的左顶点，直线过右焦点F2与椭圆C交于M、N两点。若AM、AN 的斜率满足求直线的方程.‎ ‎2016-2017上学期高三年级单元过关检测三答案 一、选择题： BDACB ABBAB ‎ 二、填空题： 11.4； 12. 2＋. 13.；14. 15. 三、解答题：‎ ‎17.解：(1)由题意可知 由 ……………………………………………3分 由………………………6分 ‎(2)由(Ⅰ)可知 即………………………………………………8分 ‎∵∴………………9分 当即时，取得最小值0………………10分 当即时，取得最大值12………………11分 ‎∴的最小值为0，此时；的最大值为12，此时……12分 ‎18．⑴ 证明：∵四边形MNEF、EFDC都是矩形，‎ ‎ ∴MN∥EF, EF∥CD,MN＝EF＝CD.‎ ‎ ∴四边形MNCD是平行四边形，……………………2分 ‎ ∴NC∥MD, ‎ ‎∵ NC平面MFD,MD平面MFD，……………………4分 ‎ ∴NC∥平面MFD ……………………5分 ‎⑵ 证明：连接ED，设ED∩FC＝O。‎ ‎∵ 平面MNEF平面ECDF，且NEEF, 平面MNEF∩平面ECDF=EF ‎ NEÌ平面ECDF, ‎ ‎∴ NE平面ECDF …………7分 ‎∵FC平面ECDF,‎ ‎∴FCNE ‎ ‎∵EC＝CD,所以四边形ECDF为正方形，‎ ‎∴FCED………9分 又ED∩NE＝E, ED,NEÌ平面NED, ‎ ‎∴FC平面NED ………11分 ‎ 又∵ND平面NED，‎ ‎ ∴NDFC ……………12分 ‎19．解：⑴ 当n＝1时，a1＝s1＝21－1＝1;‎ ‎ 当n≥2时，an＝Sn－Sn－1＝(2n－1)－(2n－1－1)＝2n－1 …………3分 ‎ 因为a1＝1适合通项公式an＝2n－1,所以an＝2n－1(nN*) …………4分 ‎⑵ 因为bn＋1－2bn＝8an,所以bn＋1－2bn＝2n＋2 即， …………6分 ‎,所以是首项为1，公差为2的等等差数列。 …………7分 ‎ 所以，所以bn＝(2n－1)×2n ……………8分 ‎ ‎ ‎ 21.解：（1）由题意椭圆的离心率 ‎∴∴∴‎ ‎∴椭圆方程为 ………………3分 又点（1，）在椭圆上，∴∴=1‎ ‎∴椭圆的方程为 ………………6分 ‎ （2）若直线斜率不存在，显然不合题意；‎ 则直线l的斜率存在。 ……………………7分 设直线为，直线l和椭交于，。‎ 将 依题意：……………………………9分 由韦达定理可知： ………………10分 又 而 从而 ………………13分 求得符合 故所求直线MN的方程为： ………………14分