2018-2019学年河南省豫南九校联考高一上学期期末考试数学试题(解析版)
2018-2019学年河南省豫南九校联考高一上学期期末考试数学试题
一、单选题
1.同学们,当你任意摆放手中笔的时候,那么桌面所在的平面一定存在直线与笔所在的直线
A.平行 B.相交 C.异面 D.垂直
【答案】D
【解析】由题设条件可知,可以借助投影的概念对及三垂线定理选出正确选项.
【详解】
解:由题意,若笔所在直线若与地面垂直,则在地面总有这样的直线,使得它与笔所在直线垂直;若笔所在直线若与地面不垂直,则其必在地面上有一条投影线,在平面中一定存在与此投影线垂直的直线,由三垂线定理知,与投影垂直的直线一定与此斜线垂直,
综上,当你任意摆放手中笔的时候,那么桌面所在的平面一定存在直线与笔所在的直线垂直.
故选:D.
【点睛】
本题考查空间中直线与平面之间的位置关系,解题的关键是熟练掌握线面垂直与三垂线定理,再结合直线与地面位置关系的判断得出答案.
2.已知直线l经过点,且斜率为,则直线l的方程为
A. B.
C. D.
【答案】A
【解析】直线经过点,且斜率为,则 即
故选A
3.若线段AB的长等于它在平面内的射影长的2倍,则AB所在直线与平面所成的角为
A. B. C. D.
【答案】C
【解析】根据图形找到线面角,进而在直角三角形中求解即可.
【详解】
如图,AC⊥α,AB∩α=B,则BC是AB在平面α内的射影,则BC=AB,所以∠ABC=60°,它是AB与平面α所成的角.故选C.
【点睛】
本题主要考查了线面角的求解,属于基础题.
4.下列函数中,满足的单调递增函数是
A. B. C. D.
【答案】A
【解析】根据题意,由依次分析选项,综合即可得答案.
【详解】
解:根据题意,依次分析选项:
对于A,对于,有,满足,符合题意;
对于B,,为对数函数,不满足,不符合题意;
对于C,,为指数函数,不满足,不符合题意;
对于D,,为指数函数,不满足,不符合题意;
故选:A.
【点睛】
本题考查函数的值的计算,涉及函数单调性的判断,属于基础题.
5.若直线:过点,:,则直线与
A.平行 B.相交但不垂直
C.垂直 D.相交于点
【答案】C
【解析】利用直线:过点,求出a,求出两条直线的斜率,即可得出结论.
【详解】
解:直线:过点,
,
,
直线:的斜率为2,
:的斜率为,
直线与:互相垂直.
故选:C.
【点睛】
本题考查直线方程,考查直线与直线的位置关系,考查学生的计算能力,比较基础.
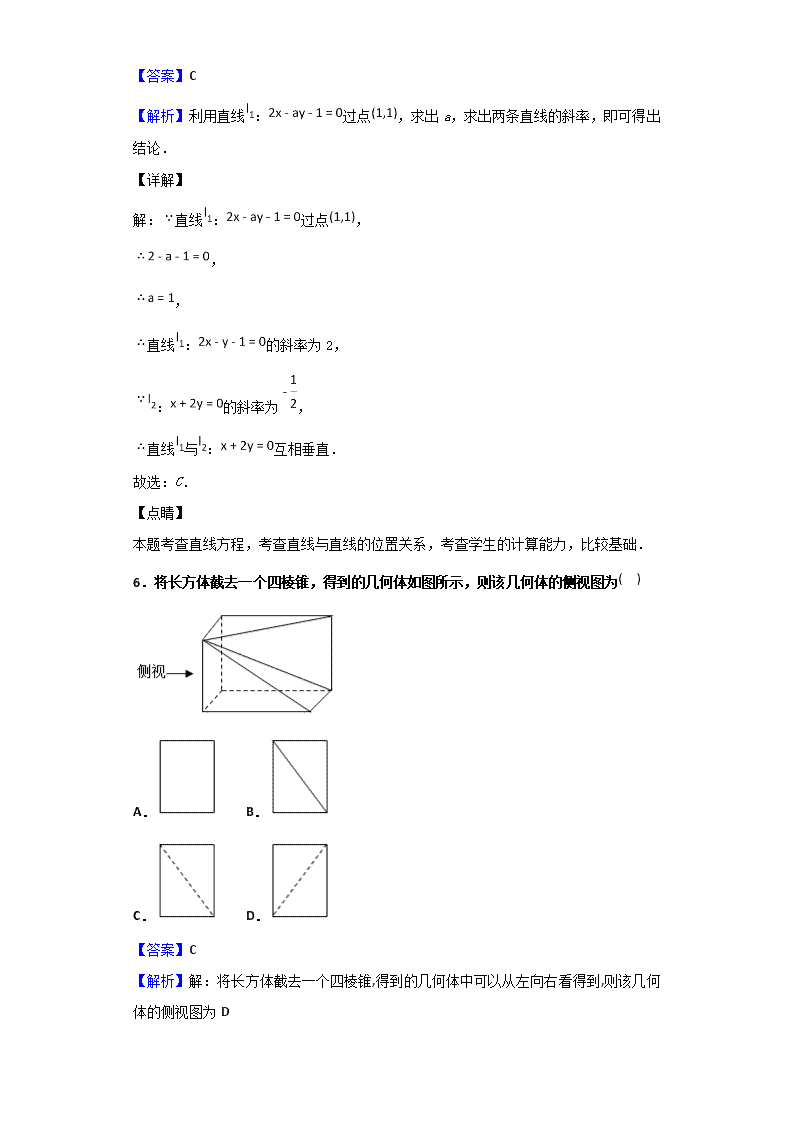
6.将长方体截去一个四棱锥,得到的几何体如图所示,则该几何体的侧视图为
A. B.
C. D.
【答案】C
【解析】解:将长方体截去一个四棱锥,得到的几何体中可以从左向右看得到,则该几何体的侧视图为D
7.已知函数,则=( )
A.4 B. C. D.
【答案】B
【解析】根据分段函数的解析式,代入求解,即可得到答案.
【详解】
由题意,函数,则,
所以,选B.
【点睛】
本题主要考查了分段函数的求值问题,其中解答中正确把握分段函数的解析式,根据分段条件代入求解是解答的关键,着重考查了推理与运算能力,属于基础题.
8.如图是一个正方体的平面展开图,则在正方体中直线AB与CD的位置关系为
A.相交 B.平行 C.异面而且垂直 D.异面但不垂直
【答案】D
【解析】解:利用展开图可知,线段AB与CD是正方体中的相邻两个面的面对角线,仅仅异面,所成的角为600,因此选D
9.已知函数,且,当时,,方程表示的直线是
A. B.
C. D.
【答案】C
【解析】∵f(x)=ax,且x<0时,f(x)>1,
∴0
1.
又∵y=ax+在x轴、y轴上的截距分别为-和,且|-|>,故C项图符合要求.
10.如图,在四面体ABCD中,截面PQMN是正方形,则在下列命题中,错误的是( )
A. B.截面PQMN
C. D.异面直线PM与BD所成的角为
【答案】C
【解析】首先由正方形中的线线平行推导线面平行,再利用线面平行推导线线平行,这样就把AC、BD平移到正方形内,即可利用平面图形知识做出判断.
【详解】
解:因为截面PQMN是正方形,所以、,
则平面ACD、平面BDA,
所以,,
由可得,故A正确;
由可得截面PQMN,故B正确;
异面直线PM与BD所成的角等于PM与QM所成的角,故D正确;
综上C是错误的.
故选:C.
【点睛】
本题主要考查线面平行的性质与判定.
11.已知在上的减函数,则实数a的取值范围是
A. B. C. D.
【答案】B
【解析】先将函数转化为,,两个基本函数,再利用复合函数的单调性求解.
【详解】
解:令,,
若,则函,是减函数,
由题设知为增函数,需,故此时无解;
若,则函数是增函数,则t为减函数,
需且,可解得
综上可得实数a 的取值范围是
故选:B.
【点睛】
本题考查复合函数的单调性,关键是分解为两个基本函数,利用同增异减的结论研究其单调性,再求参数的范围.
12.九章算术是我国古代著名数学经典其中对勾股定理的论述比西方早一千多年,其中有这样一个问题:“今有圆材埋在壁中,不知大小以锯锯之,深一寸,锯道长一尺问径几何?”其意为:今有一圆柱形木材,埋在墙壁中,不知其大小,用锯去锯该材料,锯口深一寸,锯道长一尺问这块圆柱形木料的直径是多少?长为1丈的圆柱形木材部分镶嵌在墙体中,截面图如图所示阴影部分为镶嵌在墙体内的部分已知弦尺,弓形高寸,估算该木材镶嵌在墙中的体积约为( )(注:1丈尺寸,,)
A.600立方寸 B.610立方寸 C.620立方寸 D.633立方寸
【答案】D
【解析】由三角形,利用勾股定理可得半径,进而得,再利用,乘以高即可得体积.
【详解】
连接,设⊙的半径为,
则,所以.
由于,
所以,即.
所以 平方寸.
∴该木材镶嵌在墙中的体积为立方寸,
故选D.
【点睛】
本题主要考查了垂径定理和勾股定理及扇形的面积公式,柱体的体积公式,属于中档题
二、填空题
13.已知直线,则直线恒经过的定点______.
【答案】
【解析】试题分析:将直线化简为点斜式,可得,∴直线经过定点,且斜率为.即直线恒过定点.故答案为:.
【考点】恒过定点的直线.
【方法点晴】本题给出含有参数的直线方程,求直线经过的定点坐标.着重考查了直线的基本量与基本形式等知识,属于基础题;如果一条直线经过某一定点,那么这条直线就是过该定点的直线.这里面可以看出,过一个定点的直线是不唯一的,事实上是由无数条直线组成,将直线化简成点斜式的形式得:,可得直线的斜率为且经过定点,从而得到答案.
14.在中,,,,平面ABC,,M是AB上一个动点,则PM的最小值为______.
【答案】
【解析】要使PM的最小,只需CM最小即可,作于H,连PH,根据线面垂直的性质可知,PH为PM的最小值,在直角三角形PCH中求出PH即可.
【详解】
解:如图,作于H,连PH,
面ABC,
,PH为PM的最小值,
而,,
.
故答案为:
【点睛】
本题主要考查了点、线、面间的距离计算,考查了空间想象能力,推理论证的能力,属于基础题.
15.已知集合,集合,则__.
【答案】
【解析】解对数不等式得:A=,求指数函数值域有:B=,再利用交集及其运算可得解,
【详解】
解:解不等式:log2(2x-4)≤1得:0<2x-4≤2,即:2<x≤3,即A=,
由y=()x,x,求其值域得:0<y,即B=,
即A∩B=,
故答案为:.
【点睛】
本题考查了解对数不等式、求指数函数值域及交集及其运算,属简单题
16.平面以任意角度截正方体,所截得的截面图形可以是_____填上所有你认为正确的序号
正三边形 正四边形 正五边形 正六边形 钝角三角形 等腰梯形 非矩形的平行四边形
【答案】
【解析】正方体有六个面,用平面去截正方体时最多与六个面相交得正六边形,最少与三个面相交得正三边形,因此用一个平面去截一正方体,截面可能为正三边形,正四边形,正六边形,等腰梯形,非矩形的平行四边形.
【详解】
解:画出截面图形如图:
可以画出三边形,但不能画出直角三角形和钝角三角形,故正确,错误;
可以画出正四边形,故正确;
经过正方体的一个顶点去切就可得到五边形但此时不可能是正五边形,故错误;.
正方体有六个面,用平面去截正方体时最多与六个面相交得六边形,且可以画出正六边形,故正确;
可以画出梯形但不是直角梯形,故正确.
可以画出非矩形的平行四边形,故.
故平面以任意角度截正方体,所截得的截面图形可以是:正三边形,正四边形,正六边形,等腰梯形,非矩形的平行四边形.
故答案为:.
【点睛】
本题考查平面截正方体的截面图形的判断,考查棱柱的结构特征等基础知识,考查学生的空间想象能力,考查运算求解能力,是中档题.
三、解答题
17.已知直线l的方程为,直线与l平行且与两坐标轴围成的三角形的面积为4,求直线的方程.
【答案】.
【解析】由题意可设直线的方程为:,可得与两坐标轴的交点,利用三角形面积计算公式即可得出.
【详解】
解:由题意可设直线的方程为:,
可得与两坐标轴的交点分别为:,
则,解得.
直线的方程为:.
【点睛】
本题考查了相互平行的直线斜率之间的关系、直线与坐标轴的交点、三角形面积计算公式,考查了推理能力与计算能力,属于基础题.
18.设函数.
当时,求函数的零点.
当时,恒成立,求m的最大值.
【答案】(1)的零点为1或;(2)3
【解析】求得的解析式,令,解方程可得所求零点;
由题意可得在的最小值,由二次函数的单调性可得最小值,即可得到所求m的最大值.
【详解】
解:时,,
由,可得或,
则的零点为1或;
当时,恒成立,
可得在的最小值,
由在递增,可得函数y的最小值为3,
即有,即m的最大值为3.
【点睛】
本题考查二次函数的零点和二次不等式恒成立问题解法,注意运用转化思想,考查运算能力,属于基础题.
19.(10分)四面体ABCD及其三视图如图所示,平行于棱AD,BC的平面分别交四面体的棱AB,BD,DC,CA于点E,F,G,H.
(1)求四面体ABCD的体积;
(2)证明:四边形EFGH是矩形.
【答案】(1);(2)详见解析
【解析】试题分析:(Ⅰ)证明AD⊥平面BDC,即可求四面体ABCD的体积;(Ⅱ)证明四边形EFGH是平行四边形,EF⊥HG,即可证明四边形EFGH是矩形
试题解析:(1)由该四面体的三视图可知,
BD⊥DC,BD⊥AD,AD⊥DC,
BD=DC=2,AD=1,
∴AD⊥平面BDC.
∴四面体体积
V=××2×2×1=
(2)证明:∵BC∥平面EFGH,
平面EFGH∩平面BDC=FG,
平面EFGH∩平面ABC=EH,
∴BC∥FG,BC∥EH.∴FG∥EH.
同理EF∥AD,HG∥AD,
∴EF∥HG.
∴四边形EFGH是平行四边形.
又∵AD⊥平面BDC,
∴AD⊥BC.∴EF⊥FG.
∴四边形EFGH是矩形.
【考点】1.直线与平面垂直的性质;2.棱柱、棱锥、棱台的体积
20.已知的顶点,AB边上的中线CM所在直线方程为边上的高BH所在直线为求:
顶点C的坐标;
直线BC的方程.
【答案】(1);(2)
【解析】试题分析:(1)点是直线与的交点,所以第一步先求直线的方程,利用过定点,和与已知直线垂直,第二步,就求两直线的交点;(2)这一问主要求点的坐标,所以设,代入直线方程,然后求的中点,代入直线方程,最后解方程,根据两点求直线方程.
试题解析:解:(1)直线AC的方程为: y﹣1=﹣2(x﹣5),即2x+y﹣11=0,
解方程组得则C点坐标为(4,3).
(2)设B(m,n),则M(,),,
整理得,解得则B点坐标为(﹣1,﹣3),y﹣3=(x﹣4),即直线BC的方程6x﹣5y﹣9=0.
【考点】1.求直线方程;2.垂直;2.中点.
21.已知四棱锥的底面为菱形,且,,,O为AB的中点.
(1)求证:平面ABCD;
(2)求点D到面AEC的距离.
【答案】⑴见证明;⑵
【解析】试题分析:(Ⅰ)求证EO⊥平面ABCD,只需证明垂直平面内的两条直线即可,注意到,则为等腰直角三角形,是的中点,从而得,由已知可知为边长为2的等边三角形,可连接CO,利用勾股定理,证明EO⊥CO,利用线面垂直的判定,可得EO⊥平面ABCD;(Ⅱ)求点D到平面AEC的距离,求点到平面的距离方法有两种,一.垂面法,二.等体积法,此题的体积容易求,且的面积也不难求出,因此可利用等体积,即,从而可求点D到面AEC的距离.
试题解析:(Ⅰ)连接CO.
∵,∴△AEB为等腰直角三角形. 1分
∵O为AB的中点,∴EO⊥AB,EO=1. 2分
又∵四边形ABCD是菱形,∠ABC=60°,
∴△ACB是等边三角形,
∴CO=. 3分
又EC=2,∴EC2=EO2+CO2,∴EO⊥CO. 4分
又CO⊂平面ABCD,EO平面ABCD,∴EO⊥平面ABCD. 6分
(Ⅱ)设点D到平面AEC的距离为h.
∵AE=,AC=EC=2,∴S△AEC=. 8分
∵S△ADC=,E到平面ACB的距离EO=1,VD-AEC=VE-ADC, 9分
∴S△AEC·h=S△ADC·EO,∴h=, 11分
∴点D到平面AEC的距离为. 12分
【考点】线线垂直的判定、线面垂直的判定,以及棱锥的体积公式,点到平面距离.
22.已知函数.
判断并证明在上的单调性;
若存在使得在上的值域为求实数a的取值范围.
【答案】(1)见解析; (2).
【解析】(1)利用定义法证明在上的单调性即可;
(2)由(1)可得在上单调递增,若存在由题可得即在区间上有两个不同的根. 列出不等式组求解即可.
【详解】
(1)
、
所以在上的单调递增.
(2)因为在上的单调递增,
所以若存在使得在上的值域为则有
也就是即在区间上有两个不同的根. …….8分
令要使在区间上有两个不同的根,
只需解得则实数的取值范围为
【点睛】
本题为函数单调性的证明,并利用单调性来解决问题,把方程有两实根转化为二次函数问题是解决问题的关键,属中档题.