- 2021-06-22 发布 |
- 37.5 KB |
- 10页


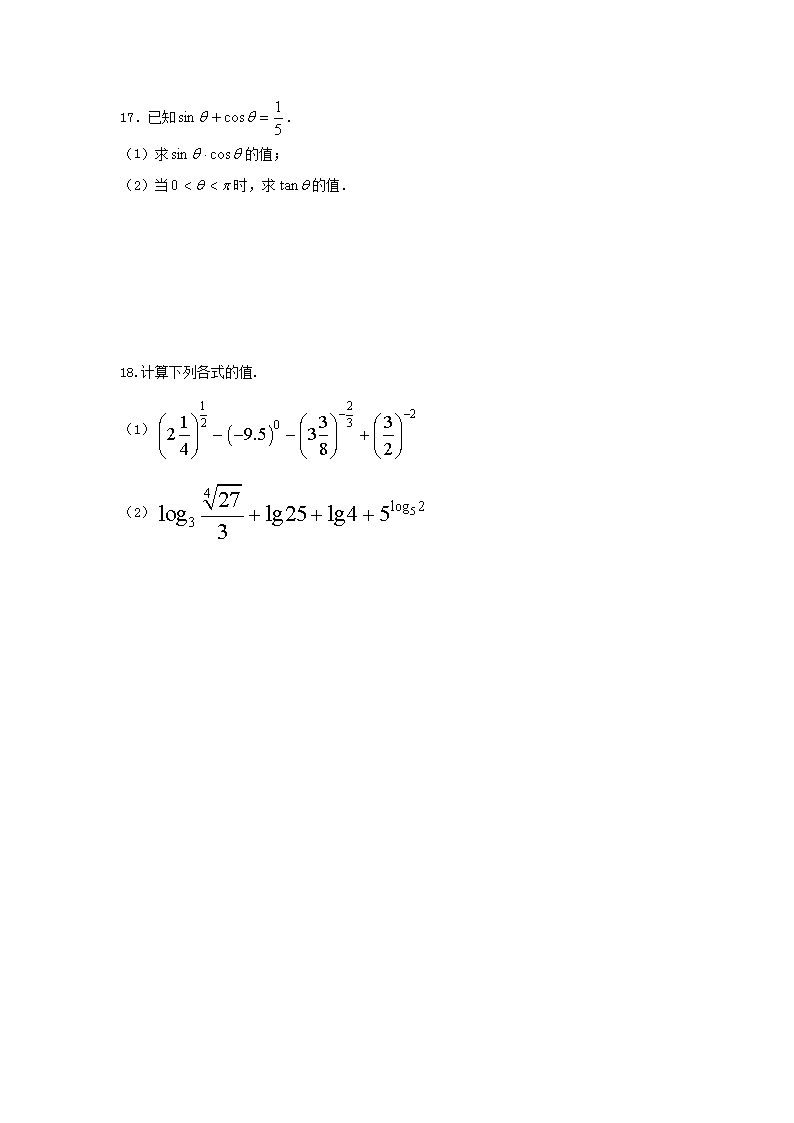
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
2018-2019学年江苏省盐城市伍佑中学高一上学期期中考试数学试题
2018-2019学年江苏省盐城市伍佑中学高一上学期期中考试数学试题 时间:120分钟 总分:160分 一、填空题: 1.集合A={1,2},B={2,3},则A∩B= . 2.6弧度是第 象限角. 3.函数的定义域为 . 4.若扇形的弧长为6cm,圆心角为2弧度,则扇形的面积为 cm2. 5.若幂函数y=(∈R)的图象经过点(4,2),则的值为 . 6.若函数在上是减函数,则实数的取值范围是 . 7.已知f(x)是R上的奇函数,当x>0时,f(x)=,则f(﹣9)= . 8.设a=,b=,c=,则a、b、c由小到大的顺序是 . 9.已知函数是定义在的偶函数,则 . 10.已知函数则的值是____. 11.若函数在区间上存在零点,则的值等于 . 12.设是定义在R上的奇函数,且,若不等式对区间的两不相等的实数都成立,则不等式的解集是____. 13.已知函数f(x)=错误!未找到引用源。是 (-∞,+∞)上的单调减函数,那么实数的取值范围是 . 14.对于实数和,定义运算“*”:, 设,且关于的方程为f(x)=m(m∈R)恰有三个互不相等的实数根,则的取值范围是_____________. 二、解答题: 15.已知集合。 (1)当时,求; (2)若,求实数的取值范围。 16.在平面直角坐标系中,角α的顶点在原点,始边在x轴的正半轴上,终边经过 点P(1,2). (1)求tanα的值; (2)求的值. 17.已知. (1)求的值; (2)当时,求的值. 18.计算下列各式的值. (1) (2) 19.某校学生社团心理学研究小组在对学生上课注意力集中情况的调查研究中,发现其注意力指数与听课时间之间的关系满足如图所示的曲线。当时,曲线是二次函数图象的一部分; 当8100 O00 1200 1400 45 8200 时,曲线是函数图象的一部分。根据专家研究,当注意力指数大于或等于80时听课效果最佳。 (1) 试求的函数关系式; (2) 老师在什么时段内安排核心内容能使得学生听课效果最佳? 请说明理由。 20.已知函数, (1)若是函数的两个零点,且函数的最小值为, ①试探求是否为定值,并给出理由; ②若存在,试确定实数的取值范围; (2)若方程的两实根为,当且时,求实数的取值范围。 盐城市伍佑中学 2018-2019学年度第一学期高一年级期中考试 数学试卷2018.11.20 时间:120分钟 总分:160分 命题: 1.集合A={1,2},B={2,3},则A∩B= .1.{2} 2.6弧度是第 象限角.2.四 3.函数f(x)=log2(1﹣x)的定义域为 .3.{x|x<1} 4.若扇形的弧长为6cm,圆心角为2弧度,则扇形的面积为 cm2.4.9 5.若幂函数y=xa(a∈R)的图象经过点(4,2),则a的值为 .5. 6.若函数在上是减函数,则实数a的取值范围是 . 6. 7.已知f(x)是R上的奇函数,当x>0时,f(x)=,则f(﹣9)= .7.﹣3 8.设a=log0.60.8,b=ln0.8,c=20.8,则a、b、c由小到大的顺序是 .b<a<c 9.已知函数是定义在的偶函数,则 .9. 10.已知函数,则的值是____. 10. 11.若函数在区间上存在零点,则的值等于 .11.2 12.设是定义在上的奇函数,且,若不等式对区间的两不相等的实数都成立,则不等式的解集是____. 12. 13.已知函数f(x)=错误!未找到引用源。是(-∞,+∞)上的单调减函数,那么实数 的取值范围是 . 14.对于实数和,定义运算“*”:, 设,且关于的方程为f(x)=m(m∈R)恰有三个互不相等的实数根,则的取值范围是_____________. 15.已知集合。 (1)当时,求; (2)若,求实数的取值范围。 15.解析:(1)当时, 所以………3分 因为 所以………7分 (2)因为,所以………9分 因为 所以,………11分 解得,………13分 即的取值范围是………14分 16在平面之间坐标系中,角α的终边经过点P(1,2). (1)求tanα的值; (2)求的值. 16.【解答】解:(1)∵角α的终边经过点P(1,2), ∴x=1,y=2,则tanα==2; (2)∵角α的终边经过点P(1,2), ∴sinα=,cosα=, 则==. 17.已知. (1)求的值; (2)当时,求的值. 17.解:(1) . (2)因为且 所以 由 得. 18.计算下列各式的值. (1) (2) 18.【答案】(1);(2). 【解析】(1) (2) 8100 O00 1200 1400 45 8200 19、某校学生社团心理学研究小组在对学生上课注意力集中情况的调查研究中,发现其注意力指数与听课时间之间的关系满足如图所示的曲线。当时,曲线是二次函数图象的一部分; 当时,曲线是函数 图象的一部分。根据专家研究,当注意力指数大于或等于80时听课效果最佳。 (1) 试求的函数关系式; (2) 老师在什么时段内安排核心内容能使得学生听课效果最佳? 请说明理由。 解答:(1)时,设(),将代入得 时, ……4分 时,将代入,得 ……6分 ∴ ……8分 (2)时,,解得,∴ …………12分 时,,解得, ∴ …………15分 综上,老师在时段内安排核心内容能使得学生听课效果最佳. …………16分 20、已知函数, (1)若是函数的两个零点,且函数的最小值为, ①试探求是否为定值,并给出理由; ②若存在,试确定实数的取值范围; (2)若方程的两实根为,当且时,求实数的取值范围。 解:(1)①由,得, ∴, 所以 ………………4分 ②,从而有, ∴或从而有, ………………6分 ∴,, ∵,∴,得,∴ 所以,的取值范围为 ………………10分 (2)由得,令, 由的实根为,知,故同号, (Ⅰ)若,则,故, ∴,即,即, 又,即, ∴, 解得; ………………13分 (Ⅱ)若,则,∴,即,即, ∴,解得. 综上所述,得或 ………………16分查看更多