数学（理）卷·2018届湖南省衡阳市八中高三（实验班）上学期第二次月考（2017

数学（理）卷·2018届湖南省衡阳市八中高三（实验班）上学期第二次月考（2017

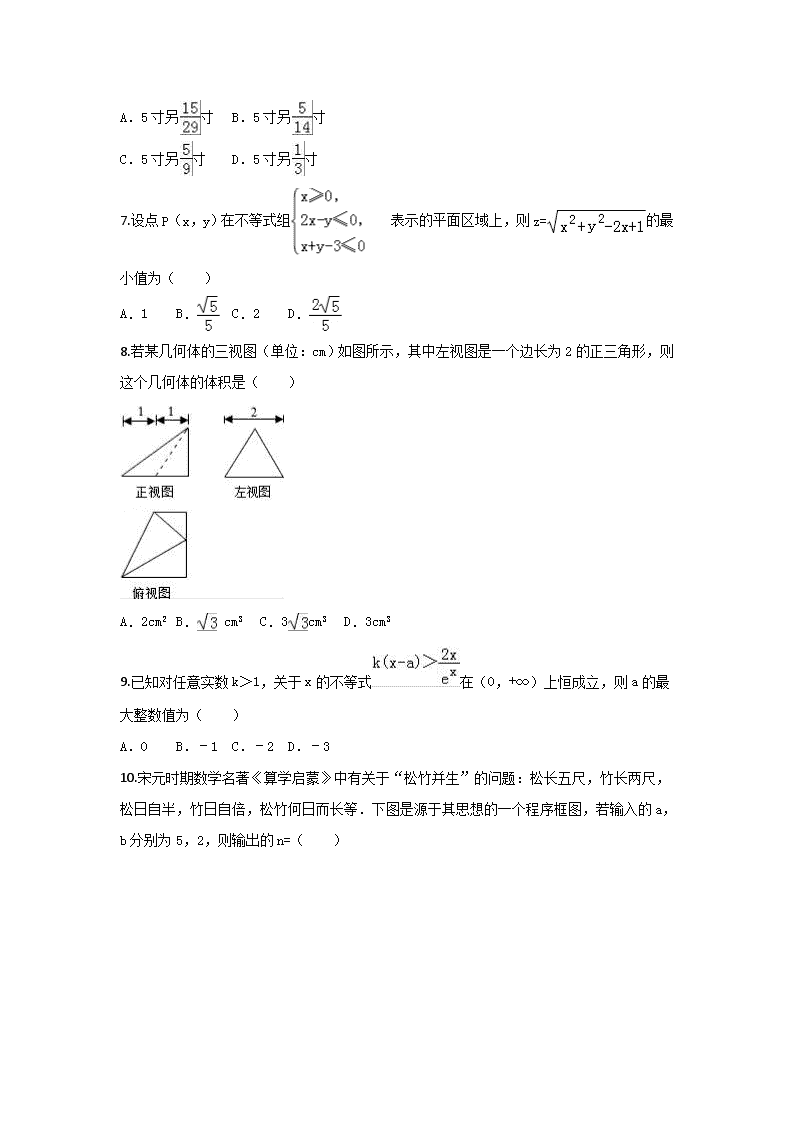
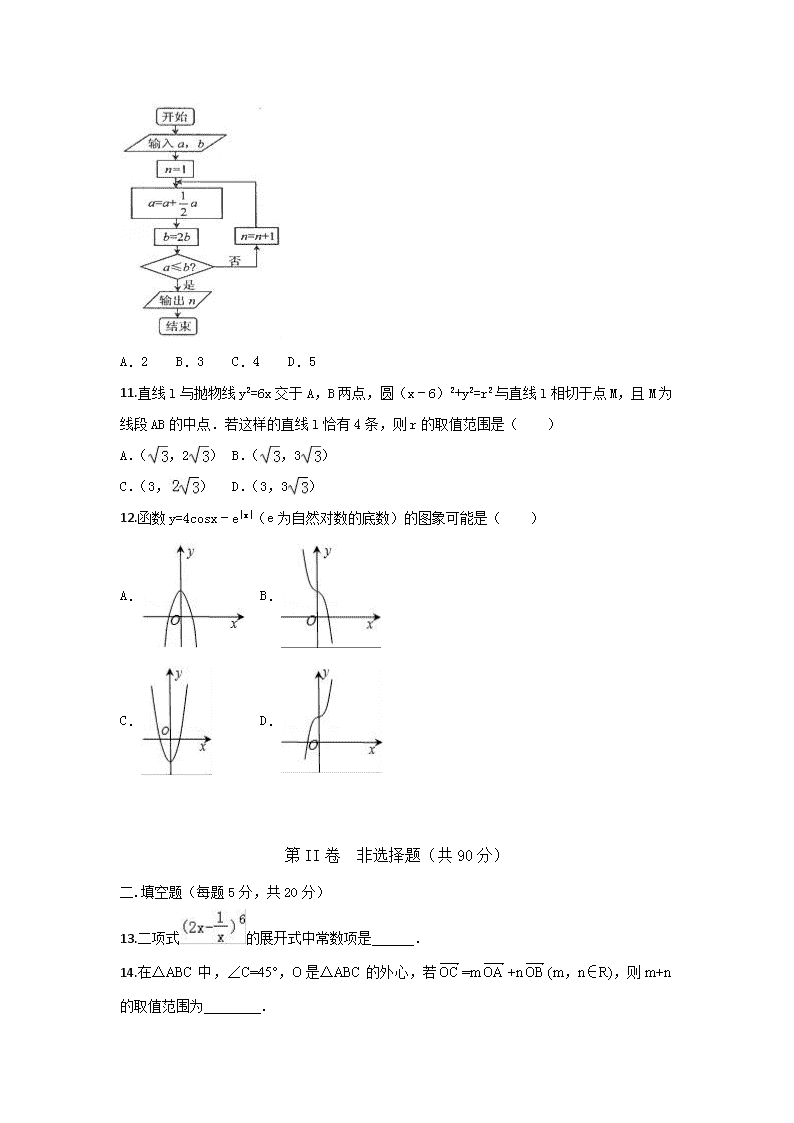
衡阳八中2017-2018学年高三上学期第二次月考试卷 理数（试题卷）‎ 注意事项：‎ ‎1.本卷为衡阳八中高三年级实验班第二次月考试卷，分两卷。其中共22题，满分150分，考试时间为120分钟。‎ ‎2.考生领取到试卷后，应检查试卷是否有缺页漏页，重影模糊等妨碍答题现象，如有请立即向监考老师通报。开考15分钟后，考生禁止入场，监考老师处理余卷。‎ ‎3.请考生将答案填写在答题卡上，选择题部分请用2B铅笔填涂，非选择题部分请用黑色‎0.5mm签字笔书写。考试结束后，试题卷与答题卡一并交回。‎ ‎★预祝考生考试顺利★‎ 第I卷 选择题（每题5分，共60分）‎ 本卷共12题，每题5分，共60分，在每题后面所给的四个选项中，只有一个是正确的。‎ ‎1.已知全集N=Z，集合A={﹣1，1，2，3，4}，B={﹣2，﹣1，0，1，2}，则（∁UA）∩B=（　　）‎ A．{3，4} B．{﹣2，3} C．{﹣2，4} D．{﹣2，0}‎ ‎2.设i为虚数单位，复数（2﹣i）z=1+i，则z的共轭复数在复平面中对应的点在（　　）‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎3.已知α为锐角，cos（α+）=，则sinα=（　　） ‎ A．B．C．D．‎ ‎4.已知0＜a＜1，x=loga+loga，y=loga5，z=loga﹣loga，则（　　）‎ A．x＞y＞z B．z＞y＞x C．y＞x＞z D．z＞x＞y ‎5.若函数f（x）=x2+x﹣lnx+1在其定义域的一个子区间（2k﹣1，k+2）内不是单调函数，则实数k的取值范围是（　　）‎ A．（﹣，） B．[，3）C．（﹣，3）D．[，）‎ ‎6.成书于公元五世纪的《张邱建算经》是中国古代数学史上的杰作，该书中记载有很多数列问题，如“今有女善织，日益功疾．初日织五尺，今一月日织九匹三丈． 问日益几何．”意思是：某女子善于织布，一天比一天织得快，而且每天增加的数量相同．已知第一天织布5尺，30天共织布390尺，则该女子织布每天增加（　　）（其中1匹=4丈，1丈=10尺，1尺=10寸）‎ A．5寸另寸 B．5寸另寸 ‎ C．5寸另寸 D．5寸另寸 ‎7.设点P（x，y）在不等式组表示的平面区域上，则z=的最小值为（　　）‎ A．1 B． C．2 D．‎ ‎8.若某几何体的三视图（单位：cm）如图所示，其中左视图是一个边长为2的正三角形，则这个几何体的体积是（　　）‎ A．‎2cm2 B． cm‎3 ‎C．‎3cm3 D．‎3cm3‎ ‎9.已知对任意实数k＞1，关于x的不等式在（0，+∞）上恒成立，则a的最大整数值为（　　）‎ A．0 B．﹣‎1 ‎C．﹣2 D．﹣3‎ ‎10.宋元时期数学名著《算学启蒙》中有关于“松竹并生”的问题：松长五尺，竹长两尺，松日自半，竹日自倍，松竹何日而长等．下图是源于其思想的一个程序框图，若输入的a，b分别为5，2，则输出的n=（　　）‎ A．2 B．‎3 ‎C．4 D．5‎ ‎11.直线l与抛物线y2=6x交于A，B两点，圆（x﹣6）2+y2=r2与直线l相切于点M，且M为线段AB的中点．若这样的直线l恰有4条，则r的取值范围是（　　）‎ A．（，2） B．（，3）‎ C．（3，） D．（3，3）‎ ‎12.函数y=4cosx﹣e|x|（e为自然对数的底数）的图象可能是（　　）‎ A． B．‎ C． D．‎ ‎           ‎ 第II卷 非选择题（共90分）‎ 二.填空题（每题5分，共20分）‎ ‎13.二项式的展开式中常数项是　 　．‎ ‎14.在△ABC中，∠C=45°，O是△ABC的外心，若=m+n(m，n∈R)，则m+n的取值范围为　 　．‎ ‎15.在三棱柱ABC﹣A1B‎1C1中侧棱垂直于底面，∠ACB=90°，∠BAC=30°，BC=1，且三棱柱ABC﹣A1B‎1C1的体积为3，则三棱柱ABC﹣A1B‎1C1的外接球的表面积为　 　．‎ ‎16.设F1，F2分别是双曲线的左、右焦点，A为双曲线的左顶点，以线段F1，F2为直径的圆O与双曲线的一个交点为P，与y轴交于B，D两点，且与双曲线的一条渐近线交于M，N两点，则下列命题正确的是　　．（写出所有正确的命题编号）‎ ‎①线段BD是双曲线的虚轴；‎ ‎②△PF‎1F2的面积为b2；‎ ‎③若∠MAN=120°，则双曲线C的离心率为；‎ ‎④△PF‎1F2的内切圆的圆心到y轴的距离为a．‎ 三.解答题（共6题，共70分）‎ ‎17.（本题满分12分）‎ 设函数f（x）=sinx（cosx﹣sinx）．‎ ‎（1）求函数f（x）在[0，π]上的单调递增区间；‎ ‎（2）设△ABC的三个角A、B、C所对的边分别为a、b、c，且f（B）=0，a、b、c成公差大于零的等差数列，求的值．‎ ‎18.（本题满分12分）‎ 如图，边长为3的正方形ABCD所在平面与等腰直角三角形ABE所在平面互相垂直，AE⊥‎ AB，且，．‎ ‎（Ⅰ）求证：MN∥平面BEC；‎ ‎（Ⅱ）求二面角N﹣ME﹣C的大小．‎ ‎ ‎ ‎19.（本题满分12分）‎ 微信是腾讯公司推出的一种手机通讯软件，它支持发送语音短信、视频、图片和文字，一经推出便风靡全国，甚至涌现出一批在微信的朋友圈内销售商品的人（被称为微商）．为了调查每天微信用户使用微信的时间情况，某经销化妆品的微商在一广场随机采访男性、女性微信用户各50名．其中每天玩微信时间超过6小时的用户列为“微信控”，否则称其为“非微信控”，调查结果如表：‎ 微信控 非微信控 合计 男性 ‎26‎ ‎24‎ ‎50‎ 女性 ‎30‎ ‎20‎ ‎50‎ 合计 ‎56‎ ‎44‎ ‎100‎ ‎（1）根据以上数据，能否有60%的把握认为“微信控”与“性别”有关？‎ ‎（2）现从参与调查的女性用户中按分层抽样的方法选出5人赠送营养面膜1份，求所抽取的5人中“微信控”和“非微信控”的人数；‎ ‎（3）从（2）中抽选取的5人中再随机抽取3人赠送价值200元的护肤品套装，记这3人中“微信控”的人数为X，试求X的分布列及数学期望．‎ 参考公式：，其中n=a+b+c+d． ‎ P（K2≥k0）‎ ‎0.50‎ ‎0.40‎ ‎0.25‎ ‎0.05‎ ‎0.025‎ ‎0.010‎ k0‎ ‎0.455‎ ‎0.708‎ ‎1.323‎ ‎3.841‎ ‎5.024‎ ‎6.635‎ ‎20.（本题满分12分）‎ 已知椭圆C： =1（a＞b＞0），定义椭圆C上的点M（x0，y0）的“伴随点”为．‎ ‎（1）求椭圆C上的点M的“伴随点”N的轨迹方程；‎ ‎（2）如果椭圆C上的点（1，）的“伴随点”为（，‎ ‎），对于椭圆C上的任意点M及它的“伴随点”N，求的取值范围；‎ ‎（3）当a=2，b=时，直线l交椭圆C于A，B两点，若点A，B的“伴随点”分别是P，Q，且以PQ为直径的圆经过坐标原点O，求△OAB的面积．‎ ‎21.（本题满分12分）‎ 已知函数f（x）=x2﹣ax（a≠0），g（x）=lnx，f（x）的图象在它与x轴异于原点的交点M处的切线为l1，g（x﹣1）的图象在它与x轴的交点N处的切线为l2，且l1与l2平行．‎ ‎（1）求a的值；‎ ‎（2）已知t∈R，求函数y=f（xg（x）+t）在x∈[1，e]上的最小值h（t）；‎ ‎（3）令F（x）=g（x）+g′（x），给定x1，x2∈（1，+∞），x1＜x2，对于两个大于1的正数α，β，存在实数m满足：α=mx1+（1﹣m）x2，β=（1﹣m）x1+mx2，并且使得不等式|F（α）﹣F（β）|＜|F（x1）﹣F（x2）|恒成立，求实数m的取值范围．‎ 选做题 请考生从22、23题中任选一题作答，并将所选题号在答题卡上填涂，共10分。‎ ‎22.（选修4-4.坐标系与参数方程）‎ 在平面直角坐标系xoy中，直线l经过点P（﹣3，0），其倾斜角为α，以原点O为极点，以x轴非负半轴为极轴，与直角坐标系xoy取相同的长度单位，建立极坐标系．设曲线C的极坐标方程为ρ2﹣2ρcosθ﹣3=0．‎ ‎（1）若直线l与曲线C有公共点，求倾斜角α的取值范围；‎ ‎（2）设M（x，y）为曲线C上任意一点，求x+y的取值范围．‎ ‎23.（选修4-5.不等式选讲）‎ 已知函数f（x）=|2x﹣1|．‎ ‎（Ⅰ）求不等式f（x）＜2的解集；‎ ‎（Ⅱ）若函数g（x）=f（x）+f（x﹣1）的最小值为a，且m+n=a（m＞0，n＞0），求的最小值．‎ 参考答案 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 D D D C B A D B B C D A ‎13.-160‎ ‎14.[﹣，1]‎ ‎15.16π ‎16.②③④‎ ‎17.‎ ‎（1）=sinxcosx﹣sin2x ‎=sin2x﹣•（1﹣cos2x）=sin（2x+）﹣，‎ 令2kπ﹣≤2x+≤2kπ+（k∈Z），得kπ﹣≤x≤kπ+（k∈Z），‎ ‎∴函数的增区间为[kπ﹣，kπ+]，k∈Z．‎ ‎∵x∈[0，π]，∴函数的增区间为[0，]，[，π]．（5分）‎ ‎（2）由（1）得，f（B）=sin（2B+）﹣=0，‎ ‎∴sin（2B+）=，‎ 由0＜B＜π得，2B+=，解得B=，‎ 由A+B+C=π得，A+C=，（7分）‎ ‎∵成公差大于零的等差数列，‎ ‎∴c＞a，b＞a，且2b=a+c，则b=，[]‎ 由余弦定理得，b2=a2+c2﹣2accosB ‎∴，‎ 化简得，，（9分）‎ 即，‎ 解得=或，‎ 又c＞a，则，‎ ‎∴由正弦定理得， =．（12分）‎ ‎18.‎ 证明：（Ⅰ）过M作MF∥DC交CE于F，连接MF，BF．‎ 因为MF∥DC，，所以．…（2分）‎ 又，所以．故，…（4分）‎ 所以四边形NBFM为平行四边形，故MN∥BF，‎ 而BF⊆平面BEC，MN⊄平面BEC，‎ 所以MN∥平面BEC；…（6分）‎ 解：（Ⅱ）以A为坐标原点，所在方向为x，y，z轴正方向，建立空间直角坐标系，‎ 直角坐标系，则E（3，0，0），N（0，1，0），‎ M（1，0，2），C（0，3，3），‎ ‎=（2，0，﹣2），=（﹣1，3，1），=（﹣2，0，2），‎ ‎=（﹣3，1，0），‎ 设平面MEC的法向量为=（x，y，z），‎ 则，取x=1，得，‎ 设平面MNE的法向量为，‎ 则，即，取x1=1，得，‎ ‎，‎ 所求二面角的大小为…（12分）‎ ‎19.‎ ‎（1）由题意，K2=≈0.65＜0.708，‎ ‎∴没有60%的把握认为“微信控”与“性别”有关；（4分）‎ ‎（2）从参与调查的女性用户中按分层抽样的方法，比例为3：2，选出5人赠送营养面膜1份，所抽取的5人中“微信控”有3人，“非微信控”的人数有2人；（7分）‎ ‎（3）X=1，2，3，则 P（X=1）==0.3， P（X=2）==0.6，P（X=3）==0.1．（9分）‎ X的分布列为：‎ X ‎1‎ ‎2‎ ‎3‎ P ‎0.3‎ ‎0.6‎ ‎0.1‎ X的数学期望为EX=1×0.3+2×0.6+3×0.1=1.8．（12分）‎ ‎20.‎ ‎（1）设N（x，y）由题意，则，‎ 又，‎ ‎∴，‎ 从而得x2+y2=1…（3分）‎ ‎（2）由，得a=2．又，得．‎ ‎∵点M（x0，y0）在椭圆上，，，且，‎ ‎•=（x0，y0）（，）=+=x02+，‎ 由于，的取值范围是[，2]…（6分）‎ ‎（3）设A（x1，y1），B（x2，y2），则；‎ ‎1）当直线l的斜率存在时，设方程为y=kx+m，由，‎ 得（3+4k2）x2+8kmx+4（m2﹣3）=0；‎ ‎ 有①…（7分）‎ 由以PQ为直径的圆经过坐标原点O可得：3x1x2+4y1y2=0；‎ 整理得：②‎ 将①式代入②式得：3+4k2=‎2m2‎，…（8分）‎ ‎3+4k2＞0，则m2＞0，△=‎48m2‎＞0，‎ 又点O到直线y=kx+m的距离，‎ 丨AB丨==×=×，‎ ‎∴…（9分）‎ ‎2）当直线l的斜率不存在时，设方程为x=m（﹣2＜m＜2）‎ 联立椭圆方程得；代入3x1x2+4y1y2=0，得，‎ 解得m2=2，从而，（10分）‎ S△OAB=丨AB丨×d=丨m丨丨y1﹣y2丨=，‎ ‎ 综上：△OAB的面积是定值．…（12分） 21.‎ ‎（1）y=f（x）图象与x轴异于原点的交点M（a，0），f′（x）=2x﹣a，‎ y=g（x﹣1）=ln（x﹣1）图象与x轴的交点N（2，0），‎ g′（x﹣1）=由题意可得k l1=k l2，即a=1；（2分）‎ ‎（2）y=f[xg（x）+t]=[xlnx+t]2﹣（xlnx+t）‎ ‎=（xlnx）2+（2t﹣1）（xlnx）+t2﹣t，‎ 令u=xlnx，在 x∈[1，e]时，u′=lnx+1＞0，‎ ‎∴u=xlnx在[1，e]单调递增，0≤u≤e，‎ u2+（2t﹣1）u+t2﹣t图象的对称轴u=，抛物线开口向上，‎ ‎①当u=≤0，即t≥时，y最小=t2﹣t，‎ ‎②当u=≥e，即t≤时，y最小=e2+（2t﹣1）e+t2﹣t，‎ ‎③当0＜＜e，即＜t＜时，‎ y最小=y|u==﹣；（5分）‎ ‎（3）F（x）=g（x）+g′（x）=lnx+，‎ F′（x）=≥0，‎ 所以F（x）在区间（1，+∞）上单调递增，‎ ‎∴当x≥1时，F（x）≥F（1）＞0，‎ ‎①当m∈（0，1）时，有，‎ α=mx1+（1﹣m）x2＞mx1+（1﹣m）x1=x1，‎ α=mx1+（1﹣m）x2＜mx2+（1﹣m）x2=x2，‎ 得α∈（x1，x2），同理β∈（x1，x2），‎ ‎∴由f（x）的单调性知 0＜F（x1）＜F（α）、f（β）＜f（x2），‎ 从而有|F（α）﹣F（β）|＜|F（x1）﹣F（x2）|，符合题设．‎ ‎②当m≤0时，‎ α=mx1+（1﹣m）x2≥mx2+（1﹣m）x2=x2，‎ β=mx2+（1﹣m）x1≤mx1+（1﹣m）x1=x1，‎ 由f（x）的单调性知，‎ F（β）≤F（x1）＜f（x2）≤F（α），‎ ‎∴|F（α）﹣F（β）|≥|F（x1）﹣F（x2）|，与题设不符，‎ ‎③当m≥1时，同理可得α≤x1，β≥x2，‎ 得|F（α）﹣F（β）|≥|F（x1）﹣F（x2）|，与题设不符，‎ ‎∴综合①、②、③得 m∈（0，1）．（12分）‎ ‎22.‎ ‎（1）将曲线C的极坐标方程ρ2﹣2ρcosθ﹣3=0‎ 化为直角坐标方程为x2+y2﹣2x﹣3=0，‎ 直线l的参数方程为（t为参数），‎ 将参数方程代入x2+y2﹣2x﹣3=0，整理得t2﹣8tcosα+12=0，‎ ‎∵直线l与曲线C有公共点，∴△=64cos2α﹣48≥0，‎ ‎∴cosα≥，或cosα≤﹣，∵α∈[0，π），‎ ‎∴α的取值范围是[0，]∪[，π）．（5分）‎ ‎（2）曲线C的方程x2+y2﹣2x﹣3=0可化为（x﹣1）2+y2=4，‎ 其参数方程为，（θ为参数），‎ ‎∵M（x，y）为曲线上任意一点，‎ ‎∴x+y=1+2cosθ+2sinθ=1+2sin（θ+），‎ ‎∴x+y的取值范围是[1﹣2，1+2]．（10分）‎ ‎23.（1）由f（x）＜2知|2x﹣1|＜2，于是﹣2＜2x﹣1＜2，解得﹣，‎ 故不等式f（x）＜2的解集为；（4分）‎ ‎（2）由条件得g（x）=|2x﹣1|+|2x﹣3|≥|2x﹣1﹣（2x﹣3）|=2，‎ 当且仅当时，其最小值a=2，‎ 即m+n=2…‎ 又，‎ 所以==，‎ 故的最小值为，‎ 此时．（10分）‎