数学文卷·2018届湖北省荆州市高二上学期期末考试（2017-01）

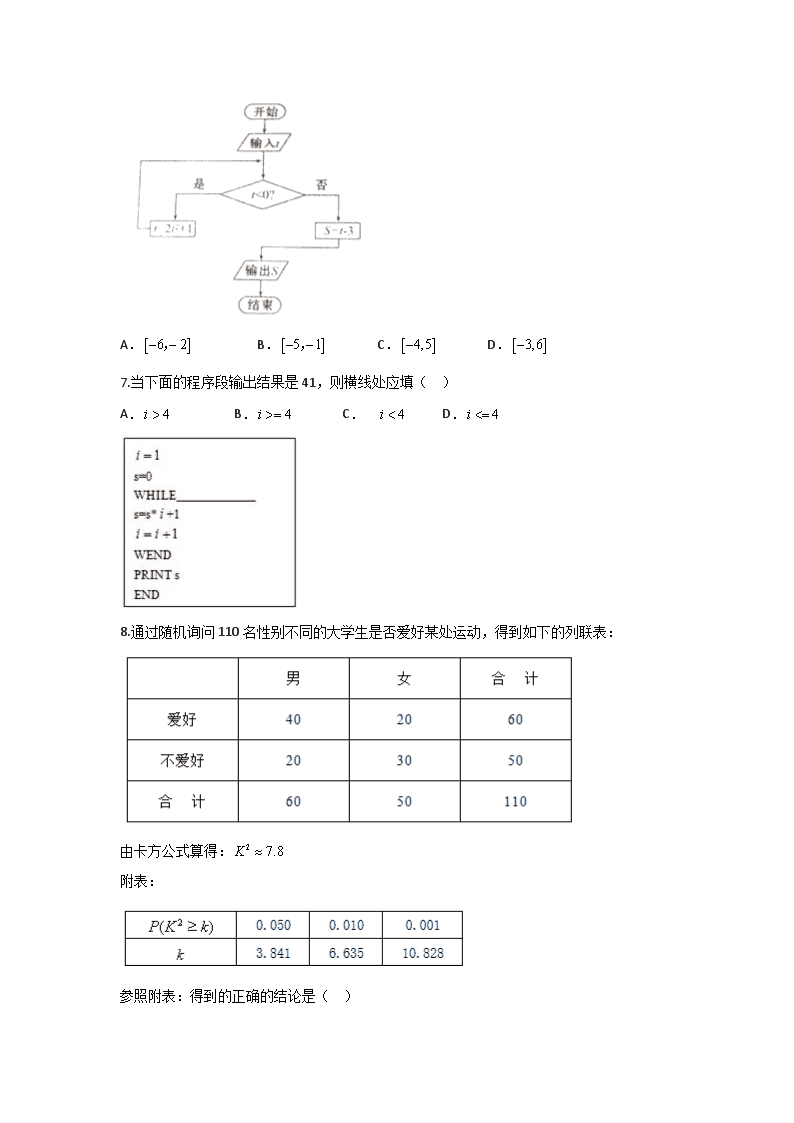
数学文卷·2018届湖北省荆州市高二上学期期末考试（2017-01）

湖北省荆州市2016-2017学年高二上学期期末考试 数学（文）试题 第Ⅰ卷（共60分）‎ 一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1.某林场有树苗30000棵，其中松树苗4000棵，为调查树苗生产情况，采用分层抽样方法抽取一个容量为150的样本，则样本中松树苗的数量为（ ） A．30 B．25 C．20 D．15‎ ‎2.在下列命题中，正确命题的个数是（ ）‎ ‎①两个复数不能比较大小；②复数对应的点在第四象限；‎ ‎③若是纯虚数，则实数；‎ ‎④若，则. A．0 B．1 C．2 D．3‎ ‎3.用“辗转相除法”求得360和504的最大公约数是（ ）‎ A．72 B．36 C．24 D．2520‎ ‎4.下面使用类比推理正确的是（ ）‎ A．“若，则”类推出“若，则” ‎ B．“若”类推出“” ‎ C．“若”类推出“” ‎ D．“若”类推出“”‎ ‎5. 已知圆内一点，则过点的直径所在的直线方程是（ ）‎ A． B． C． D．‎ ‎6.执行如图所示的程序框图，如果输入的，则输出的属于（ ）‎ ‎ A． B． C． D．‎ ‎7.当下面的程序段输出结果是41，则横线处应填（ ）‎ A． B． C． D．‎ ‎8.通过随机询问110名性别不同的大学生是否爱好某处运动，得到如下的列联表：‎ ‎ 由卡方公式算得： 附表：‎ 参照附表：得到的正确的结论是（ ） ‎ A．在犯错的概率不超过0.1%的前提下，认为“爱好该运动与性别无关” ‎ B．在犯错的概率不超过0.1%的前提下，认为“爱好该运动与性别有关” ‎ C．有99%以上的把握认为“爱好该运动与性别有关” ‎ D．有99%以上的把握认为“爱好该运动与性别无关”‎ ‎9.已知点是直线上的一动点，是圆的两条切线(为圆心)，是切点，若四边形的面积的最小值是2，则的值为（ ） A．3 B． C． D．2‎ ‎10.设某大学的女生体重(单位：)与身高(单位：)具有线性相关关系，根据一组样本数据，用最小二乘法建立的回归方程为，则下列结论中不正确的是（ ）‎ A．与具有正的线性相关关系 ‎ B．回归直线过样本点的中心 ‎ C．若该大学某女生身高增加1，则其体重约增加0.85 ‎ D．若该大学某女生身高增加170，则可断定其体重必为58.79‎ ‎11.半径为的圆的面积公式为，当时，则计算面积的流程图为（ ） ‎ ‎12.在平面直角坐标系中，点，直线，设圆的半径为1，圆心在上，若圆上存在点，使，则圆心的横坐标的取值范围为（ ）‎ A． B． C． D．‎ 第Ⅱ卷（共90分）‎ 二、填空题（每题5分，满分20分，将答案填在答题纸上）‎ ‎13.设，则虚数的实部为 ．‎ ‎14.如图是某学校一名篮球运动员在五场比赛中所得分数的茎叶图，则该运动员在这五场比赛中得分的方差为 ．‎ ‎15.若满足约束条件，则的范围是 ．‎ ‎16.“开心辞典”中有这样个问题：给出一组数，要你根据规律填出后面的第几个数，现给出一组数：，它的第8个数可以是 ．‎ 三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.） ‎ ‎17. （本小题满分12分）‎ 一个盒子里装有三张卡片，分别标记有数字1,2,3，这三张卡片除标记的数字外完全相同.随机有放回地抽取3次，每次抽取1张，将抽取的卡片上的数字依次记为.‎ ‎（1）求“抽取的卡片上的数字满足”的概率；‎ ‎（2）求“抽取的卡片上的数字不完全相同”的概率.‎ ‎18. （本小题满分12分）‎ 已知圆，直线.‎ ‎（1）求证：直线恒过定点；‎ ‎（2）判断直线被圆截得的弦何时最长、何时最短？并求截得的弦最短时的值以及最短长度.‎ ‎19. （本小题满分12分）‎ 某校100位学生期中考试语文成绩的频率分布直方图如图所示，其中成绩分组区间是：.‎ ‎（1）求图中的值；‎ ‎（2）根据频率分布直方图，估计这100名学生语文成绩的中位数；‎ ‎（3）若这100名学生的语文成绩某些分数段的人数与数学成绩相应分数段的人数之比如下表所示，求数学成绩在之外的人数.（分数可以不为整数）‎ ‎20. （本小题满分12分）‎ 已知，分别求的值，然后归纳猜想一般性结论，并证明你的结论.‎ ‎21. （本小题满分12分）‎ 已知圆，直线过定点.‎ ‎（1）若与圆相切，求的方程；‎ ‎（2）若与圆相交于两点，求的面积的最大值，并求此时直线的方程.（其中点是圆的圆心）‎ ‎22. （本小题满分10分）‎ 由经验得知，在某大商场付款处排队等候付款的人数及其概率如下表：‎ ‎（1）不多于6个人排队的概率；‎ ‎（2）至少8个人排队的概率.‎ 试卷答案 一、选择题 ‎1-5: CAACA 6-10:DDCDD 11、12：BA 二、填空题 ‎13. 0 14. 15. 16. ‎ 三、解答题 ‎17.解：（1）由题意，随机有放回的抽取3次，基本事情（1，1，1），（1，1，2），（1，1，3），（1，2，1），（1， 2，2），（1，2，3），（1，3，1），（1，3，2），（1，3，3）……（3，3，3）共有27个 又包含三个基本事件：（1，1，2），（1，2，3），2，1，3）‎ 对应的概率 ‎（2）“不完全相同”的对立事件是“完全相同”， “完全相同”包含三个基本事件：“” ‎ 所以 ‎18.（1）证明：由可得：‎ ‎，设定点为，则有： []‎ 故直线 恒过定点 ‎（2）由（1）知，直线恒过定点，直线被圆截得的弦最长时，直线过圆心；直线被圆截得的弦最短时，直线与直线垂直 直线与直线垂直时，，从而可得直线的斜率 由可得：‎ 此时，弦长为 ‎19.解：（ 1）由概率和为1可得：‎ ‎（2）区间的概率和为，则区间中还需拿出概率 的区域才到达概率为，即区间要拿出的区域，‎ 故中位数为 ‎（3）‎ 分数段 ‎5人 ‎40人 ‎30人 ‎20人 ‎5人 ‎20人 ‎40人 ‎25人 根据上表知：外的人数为：‎ ‎20.解 由f(x)= 得 f(0)+f(1)= + = f(-1)+f(2)= + = f(-2)+f(3)= + = 归纳猜想一般性结论为f(-x)+f(1+x) = 证明: f(-x)+f(1+x)= + = + ‎=+ = ‎== ‎21.解：（1）直线无斜率时，直线的方程为，此时直线和圆相切 直线有斜率时，设方程为，利用圆心到直线的距离等于半径得：，直线方程为 ‎（2）面积最大时，，，即是等腰直角三角形，由半径得：圆心到直线的距离为 设直线的方程为：，‎ 直线方程为：，‎ ‎22.解：（1）‎ ‎（2)‎