2020年高考数学(理)二轮复习讲练测 专题13 算法、推理与证明、复数（测）（原卷版）

2020年高考数学(理)二轮复习讲练测 专题13 算法、推理与证明、复数（测）（原卷版）

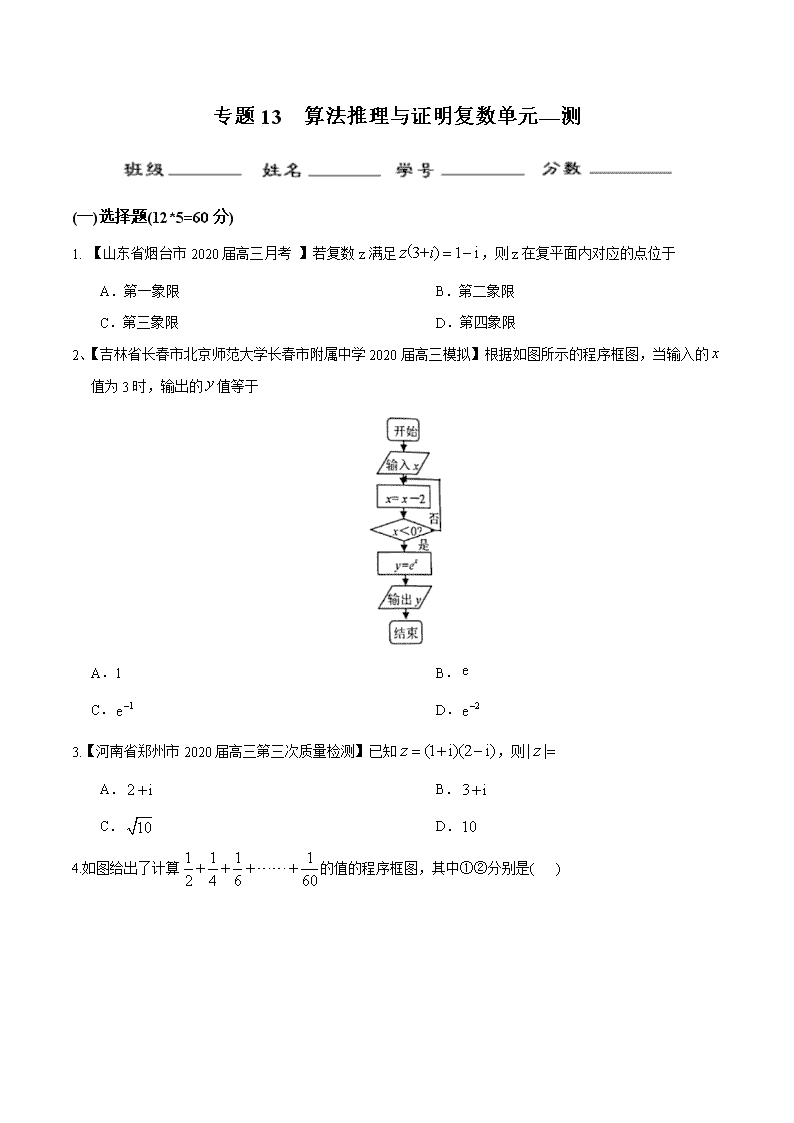
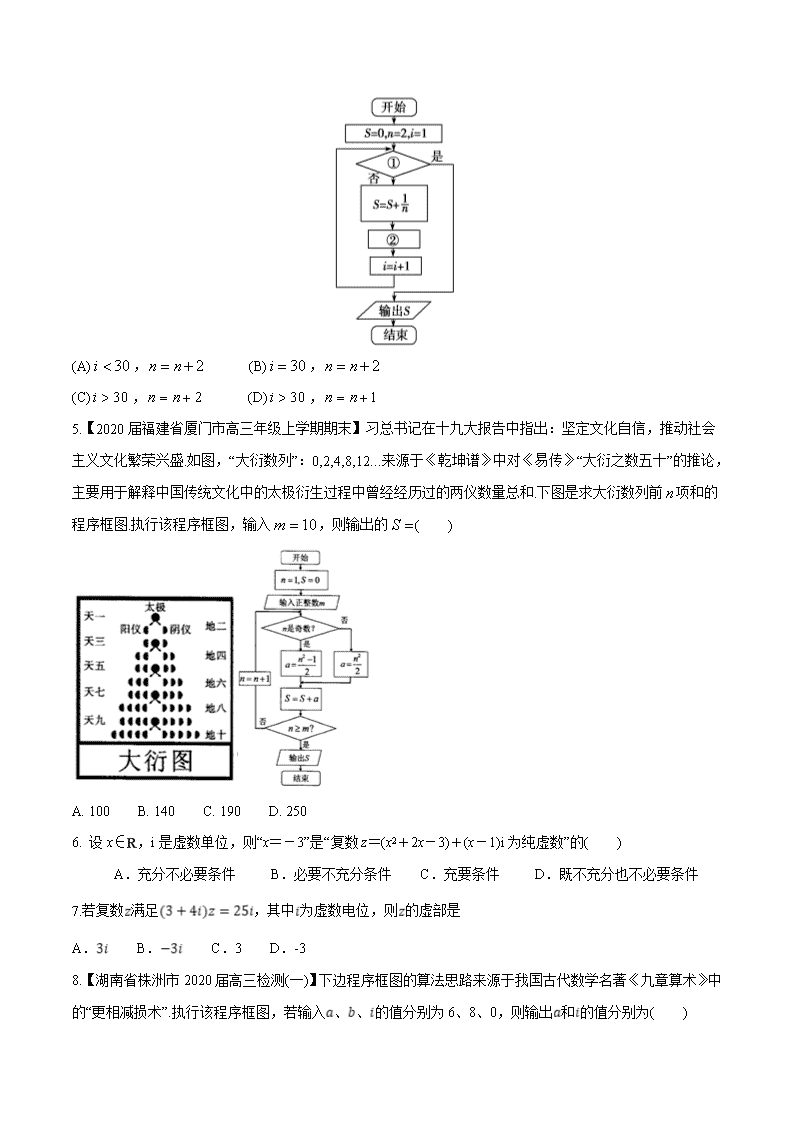
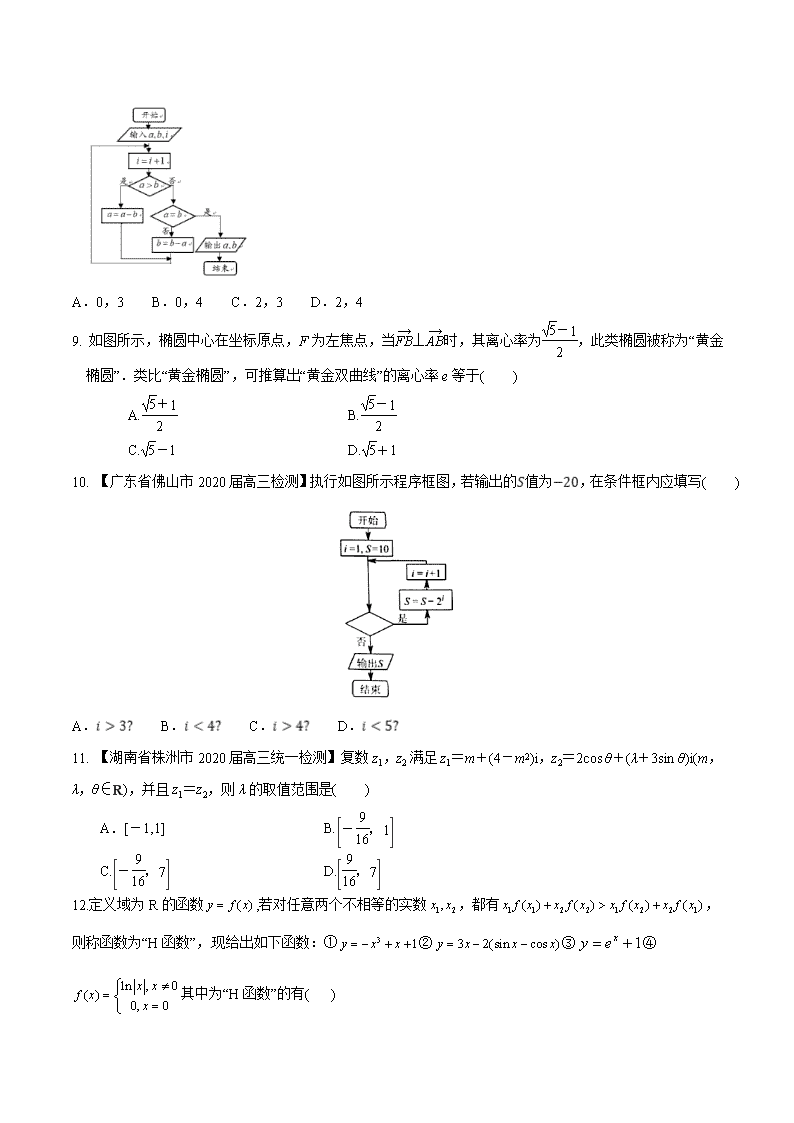
专题13 算法推理与证明复数单元—测 ‎(一)选择题(12*5=60分)‎ ‎1. 【山东省烟台市2020届高三月考 】若复数z满足，则z在复平面内对应的点位于 A．第一象限 B．第二象限 C．第三象限 D．第四象限 ‎2、【吉林省长春市北京师范大学长春市附属中学2020届高三模拟】根据如图所示的程序框图，当输入的值为3时，输出的值等于 A．1 B．‎ C． D．‎ ‎3.【河南省郑州市2020届高三第三次质量检测】已知，则 A． B．‎ C． D．‎ ‎4.如图给出了计算的值的程序框图，其中①②分别是( )‎ ‎(A)， (B)， ‎ ‎(C)， (D)，‎ ‎5.【2020届福建省厦门市高三年级上学期期末】习总书记在十九大报告中指出：坚定文化自信，推动社会主义文化繁荣兴盛.如图，“大衍数列”：0,2,4,8,12…来源于《乾坤谱》中对《易传》“大衍之数五十”的推论，主要用于解释中国传统文化中的太极衍生过程中曾经经历过的两仪数量总和.下图是求大衍数列前项和的程序框图.执行该程序框图，输入，则输出的( )‎ A. 100 B. 140 C. 190 D. 250‎ ‎6. 设x∈R，i是虚数单位，则“x＝－3”是“复数z＝(x2＋2x－3)＋(x－1)i为纯虚数”的(　　)‎ A．充分不必要条件 B．必要不充分条件 C．充要条件 D．既不充分也不必要条件 ‎7.若复数满足，其中为虚数电位，则的虚部是 A． B． C．3 D．-3‎ ‎8.【湖南省株洲市2020届高三检测(一)】下边程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图，若输入、、的值分别为6、8、0，则输出和的值分别为( )‎ A．0，3 B．0，4 C．2，3 D．2，4‎ ‎9. 如图所示，椭圆中心在坐标原点，F为左焦点，当⊥时，其离心率为，此类椭圆被称为“黄金椭圆”．类比“黄金椭圆”，可推算出“黄金双曲线”的离心率e等于(　　)‎ A. B. C.－1 D.＋1‎ ‎10. 【广东省佛山市2020届高三检测】执行如图所示程序框图，若输出的值为，在条件框内应填写( )‎ A． B． C． D．‎ ‎11. 【湖南省株洲市2020届高三统一检测】复数z1，z2满足z1＝m＋(4－m2)i，z2＝2cos θ＋(λ＋3sin θ)i(m，λ，θ∈R)，并且z1＝z2，则λ的取值范围是(　　)‎ A．[－1,1] B. C. D. ‎12.定义域为R的函数,若对任意两个不相等的实数，都有，则称函数为“H函数”，现给出如下函数：①②③④其中为“H函数”的有( )‎ A．①② B．③④ C． ②③ D． ①②③‎ ‎(二)填空题(4*5=20分)‎ ‎13.【2020届福建省厦门市高三年级第一学期期末】已知复数z1＝－1＋2i，z2＝1－i，z3＝3－4i，它们在复平面上对应的点分别为A，B，C，若＝λ＋μ，(λ，μ∈R)，则λ＋μ的值是________．‎ ‎14.执行右边的程序框图，输出的的值为 .  ‎ ‎15. 【陕西省榆林市2020届高考模拟第一次测试】我们把平面内与直线垂直的非零向量称为直线的法向量，在平面直角坐标系中，利用求动点轨迹方程的方法，可以求出过点且法向量为的直线(点法式)方程为，化简得，类比以上方法，在空间直角坐标系中，经过点且法向量为的平面(点法式)方程为__________．‎ ‎16.【四川省宜宾市叙州区2020届高三上期末】如图所示的程序框图，输出的的值为　　‎ ‎． ．2 ． ．‎ 三、解答题(共6道小题，满分70分)‎ ‎17. (10分) 如图所示，平行四边形OABC，顶点O、A、C分别表示0、3＋2i、－2＋4i，试求：‎ ‎(1)、所表示的复数；(2)对角线所表示的复数；(3)求B点对应的复数．‎ ‎18. (12分)【2020届吉林省乾安县第七中学高三模拟】已知x，y为共轭复数，且(x＋y)2－3xyi＝4－6i，求x，y.‎ ‎19. (12分) 某同学在一次研究性学习中发现，以下五个式子的值都等于同一个常数：‎ ‎①sin213°＋cos217°－sin 13°cos 17°；‎ ‎②sin215°＋cos215°－sin 15°cos 15°；‎ ‎③sin218°＋cos212°－sin 18°cos 12°；‎ ‎④sin2(－18°)＋cos248°－sin(－18°)cos 48°；‎ ‎⑤sin2(－25°)＋cos255°－sin(－25°)cos 55°.‎ ‎(1)试从上述五个式子中选择一个，求出这个常数；‎ ‎(2)根据(1)的计算结果，将该同学的发现推广为三角恒等式，并证明你的结论．‎ ‎20、等差数列{an}的前n项和为Sn，a1＝1＋，S3＝9＋3.‎ ‎(1)求数列{an}的通项an与前n项和Sn；‎ ‎(2)设bn＝(n∈N*)，求证：数列{bn}中任意不同的三项都不可能成为等比数列．‎ ‎21在平行六面体中，．‎ 求证：(1)；‎ ‎(2)．‎ ‎22. 【江苏省清江中学2020届高三调研】已知函数，记为的导数，.‎ ‎(1)求；(2)猜想的表达式，并证明你的猜想.‎