高考理科数学复习练习作业28

高考理科数学复习练习作业28

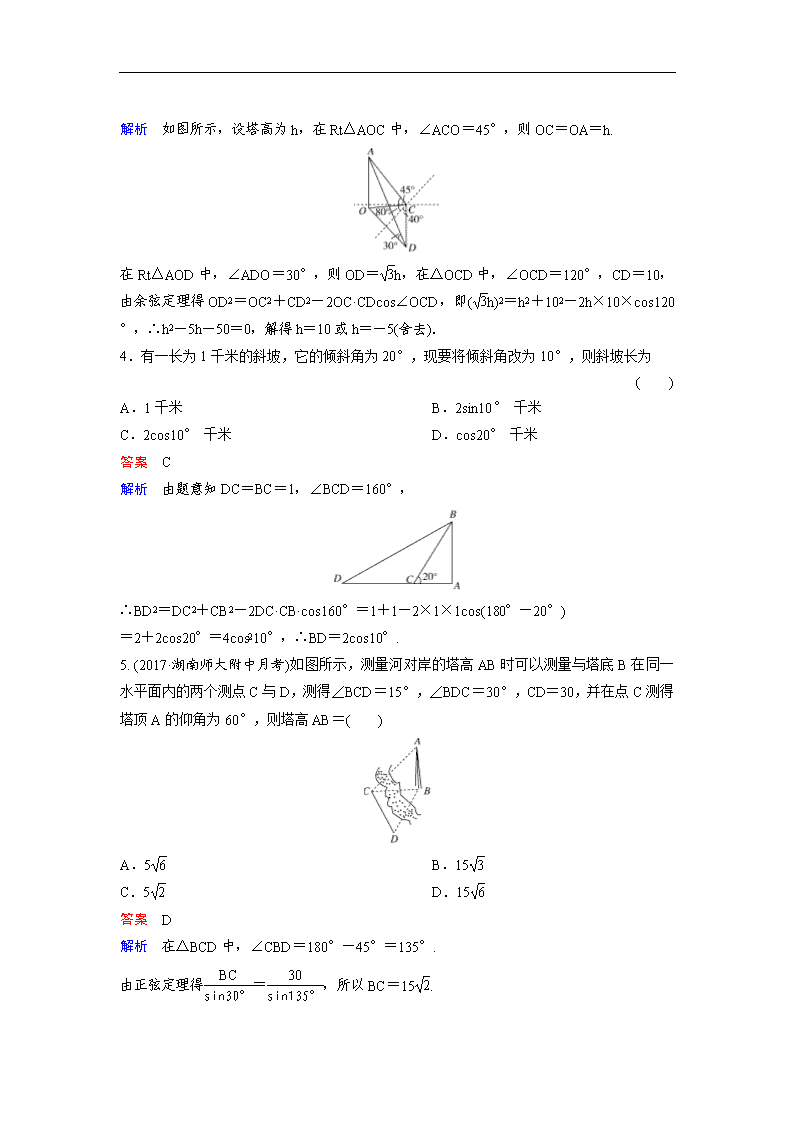
专题层级快练(二十八)‎ ‎1.如图所示，为了测量某湖泊两侧A，B间的距离，李宁同学首先选定了与A，B不共线的一点C(△ABC的角A，B，C所对的边分别记为a，b，c)，然后给出了三种测量方案：‎ ‎①测量A，C，b；②测量a，b，C；③测量A，B，a，则一定能确定A，B间的距离的所有方案的序号为(　　)‎ A．①②　　　　　　　　　 B．②③‎ C．①③ D．①②③‎ 答案　D 解析　由题意可知，在①②③三个条件下三角形均可唯一确定，通过解三角形的知识可求出AB.故选D.‎ ‎2. (2017·广东中山上学期期末)如图所示，设A，B两点在河的两岸，一测量者在A的同侧，在所在的河岸边选定一点C，测出AC的距离为50 m，∠ACB＝45°，∠CAB＝105°后，就可以计算出A，B两点的距离为(　　)‎ A．50 m B．50 m C．25 m D. m 答案　A 解析　由题意，得B＝30°.由正弦定理，得＝，∴AB＝＝＝50 (m)．故选A.‎ ‎3．某人在C点测得某塔在南偏西80°，塔顶仰角为45°，此人沿南偏东40°方向前进10米到D，测得塔顶A的仰角为30°，则塔高为(　　)‎ A．15米 B．5米 C．10米 D．1米 答案　C 解析　如图所示，设塔高为h，在Rt△AOC中，∠ACO＝45°，则OC＝OA＝h.‎ 在Rt△AOD中，∠ADO＝30°，则OD＝h，在△OCD中，∠OCD＝120°，CD＝10，由余弦定理得OD2＝OC2＋CD2－2OC·CDcos∠OCD，即(h)2＝h2＋102－2h×10×cos120°，∴h2－5h－50＝0，解得h＝10或h＝－5(舍去)．‎ ‎4．有一长为1千米的斜坡，它的倾斜角为20°，现要将倾斜角改为10°，则斜坡长为 ‎(　　)‎ A．1千米 B．2sin10° 千米 C．2cos10° 千米 D．cos20° 千米 答案　C 解析　由题意知DC＝BC＝1，∠BCD＝160°，‎ ‎∴BD2＝DC2＋CB2－2DC·CB·cos160°＝1＋1－2×1×1cos(180°－20°)‎ ‎＝2＋2cos20°＝4cos210°，∴BD＝2cos10°.‎ ‎5. (2017·湖南师大附中月考)如图所示，测量河对岸的塔高AB时可以测量与塔底B在同一水平面内的两个测点C与D，测得∠BCD＝15°，∠BDC＝30°，CD＝30，并在点C测得塔顶A的仰角为60°，则塔高AB＝(　　)‎ A．5 B．15 C．5 D．15 答案　D 解析　在△BCD中，∠CBD＝180°－45°＝135°.‎ 由正弦定理得＝，所以BC＝15.‎ 在Rt△ABC中，AB＝BCtan∠ACB＝15×＝15.故选D.‎ ‎6．在200 m高的山顶上，测得山下塔顶和塔底的俯角分别为30°，60°，则塔高为(　　)‎ A. m B. m C. m D. m 答案　A 解析　如图，在Rt△BAC中，∠ABC＝30°，AB＝200，‎ ‎∴BC＝＝.‎ ‎∵∠EBD＝30°，∠EBC＝60°，∴∠DBC＝30°，∠BDC＝120°.‎ 在△BDC中，＝.∴DC＝＝＝(m)．‎ ‎7．要测底部不能到达的电视塔AB的高度，在C点测得塔顶A的仰角是45°，在D点测得塔顶A的仰角是30°，并测得水平面上的∠BCD＝120°，CD＝40 m，求电视塔的高度．‎ 答案　40米 解析　如图设电视塔AB高为x，则在Rt△ABC中，‎ 由∠ACB＝45°，得BC＝x.在Rt△ADB中，∠ADB＝30°，∴BD＝x.‎ 在△BDC中，由余弦定理，得BD2＝BC2＋CD2－2BC·CD·cos120°.‎ 即(x)2＝x2＋402－2·x·40·cos120°，解得x＝40，∴电视塔高为40米．‎ ‎8.为了测量两山顶M，N之间的距离，飞机沿水平方向在A，B两点进行测量．A，B，M，N在同一个铅垂平面内(如图所示)．飞机能够测量的数据有俯角和A，B间的距离．请设计一个方案，包括：①指出需要测量的数据(用字母表示，并在图中标出)；②用文字和公式写出计算M，N间的距离的步骤．‎ 解析　方案一：①需要测量的数据有：A点到M，N点的俯角α1，β1，B点到M，N的俯角α2，β2；A，B间的距离d(如图所示)．‎ ‎②第一步：计算AM.由正弦定理，得AM＝；‎ 第二步：计算AN.由正弦定理，得AN＝；‎ 第三步：计算MN.由余弦定理，得 MN＝.‎ 方案二：①需要测量的数据有：A到M，N点的俯角α1，β1；B点到M，N点的俯角α2，β2；A，B间的距离d(如图所示)．‎ ‎②第一步：计算BM.由正弦定理，得BM＝；‎ 第二步：计算BN.由正弦定理，得BN＝；‎ 第三步：计算MN.由余弦定理，得 MN＝.‎ ‎9.衡水市某广场有一块不规则的绿地如图所示，城建部门欲在该地上建造一个底座为三角形的环境标志，小李、小王设计的底座形状分别为△ABC，△ABD，经测量AD＝BD＝7米，BC＝5米，AC＝8米，∠C＝∠D.‎ ‎(1)求AB的长度；‎ ‎(2)若环境标志的底座每平方米造价为5 000元，不考虑其他因素，小李、小王谁的设计使建造费用较低(请说明理由)？较低造价为多少？(＝1.732，＝1.414)‎ 答案　(1)7米　(2)小李的设计建造费用低，86 600元 解析　(1)在△ABC中，由余弦定理，得 cosC＝＝. ①‎ 在△ABD中，由余弦定理，得cosD＝. ②‎ 由∠C＝∠D，得cosC＝cosD.∴AB＝7，∴AB长为7米．‎ ‎(2)小李的设计建造费用较低，理由如下：‎ S△ABD＝AD·BD·sinD，S△ABC＝AC·BC·sinC.‎ ‎∵AD·BD>AC·BC，∴S△ABD>S△ABC.‎ 故选择△ABC建造环境标志费用较低．‎ ‎∵AD＝BD＝AB＝7，∴△ABD是等边三角形，∠D＝60°.∴S△ABC＝10＝10×1.732＝17.32.‎ ‎∴总造价为5 000×17.32＝86 600(元)．‎ ‎10．(2017·盐城一模)如图所示，经过村庄A有两条夹角为60°的公路AB，AC，根据规划拟在两条公路之间的区域内建一工厂P，分别在两条公路边上建两个仓库M，N(异于村庄A)，要求PM＝PN＝MN＝2(单位：千米)．如何设计，使得工厂产生的噪声对居民的影响最小(即工厂与村庄的距离最远)?‎ 答案　当设计∠AMN＝60°时，工厂产生的噪声对居民影响最小 解析　设∠AMN＝θ，在△AMN中，＝.‎ 因为MN＝2，所以AM＝sin(120°－θ)．‎ 在△APM中，cos∠AMP＝cos(60°＋θ)．‎ AP2＝AM2＋MP2－2AM·MP·cos∠AMP＝sin2(120°－θ)＋4－2×2×sin(120°－θ)cos(60°＋θ)＝sin2(θ＋60°)－sin(θ＋60°)cos(θ＋60°)＋4‎ ‎＝[1－cos(2θ＋120°)]－sin(2θ＋120°)＋4‎ ‎＝－[sin(2θ＋120°)＋cos(2θ＋120°)]＋ ‎＝－sin(2θ＋150°)，θ∈(0°，120°)．‎ 当且仅当2θ＋150°＝270°，即θ＝60°时，AP2取得最大值12，即AP取得最大值2.‎ 所以设计∠AMN＝60°时，工厂产生的噪声对居民影响最小．‎