数学：第二章《推理与证明复习小结》课件（新人教A版选修1-2）

数学：第二章《推理与证明复习小结》课件（新人教A版选修1-2）

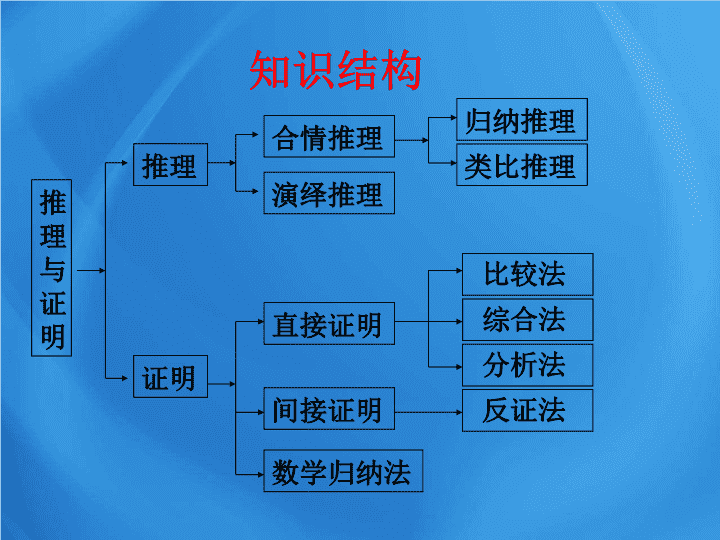
新课标人教版课件系列 《 高中数学 》 选修 1-2 第二章　推理与证明复习小结 推理与证明 推理 证明 合情推理 演绎推理 直接证明 数学归纳法 间接证明 比较法 类比推理 归纳推理 分析法 综合法 反证法 知识结构 证 为 数 为 数 证 一 . 综合法 证 为 数 为 数 证 证 证明 : 要证 只需证 只需证 只需证 只需证 因为 成立 . 所以 成立 . 二 . 分析法 三 : 反证法 问题一 : 求证 : 两条相交直线有且只有一个交点 . 注 : 1. 结论中的有且只有 ( 有且仅有 ) 形式出现 , 是唯一性问题 , 常用反证法 2. 有且只有的反面包含 1) 不存在 ;2) 至少两个 . 问题二 : 求证一元二次方程至多 ------ 有两个不相等的实根 . 注 : 所谓至多有两个 , 就是不可能有三个 , 要证 “ 至多有两个不相等的实根 ” 只要证明它的反面 “ 有三个不相等的实根 ” 不成立即可 . 问题 : 如图 ; 已知 L 1 、 L 2 是异面直线且 A 、 B ∈ L 1 ,C 、 D ∈ L 2 ,, 求证 ;AC,SD 也是异面直线 . a C D A B L 1 L 2 五 . 归纳、类比、猜想、证明 例 : 平面内有 n 条直线 , 其中任何两条不平行 , 任何三条不过同一点 , 证明交点的个数 f(n) 等于 n(n-1)/2. 证 :(1) 当 n=2 时 , 两条直线 的交点只有 1 个 , 又 f(2)=2 • (2-1)/2=1, 因此 , 当 n=2 时命题成立 . (2) 假设当 n=k(k ≥ 2) 时命题成立 , 就是说 , 平面内满足 题设的任何 k 条直线 的交点个数 f(k) 等于 k(k-1)/2. 以下来考虑平面内有 k+1 条直线的情况 . 任取其中 的 1 条直线 , 记作 l. 由归纳假设 , 除 l 以外的其他 k 条直线的 交点个数 f(k) 等于 k(k-1)/2. 另外 , 因为已知任何两条直线不平行 , 所以直线 l 必与平面内其他 k 条直线都相交 , 有 k 个交点 . 又因为已知任何三条直线不过同一点 , 所以上面的 k 个交点两两不相同 , 且与平面内其他的 k(k-1)/2 个 交点也两两不相同 . 从而平面内交点的个数是 k(k-1)/2+k=k[(k-1)+2]/2 =(k+1)[(k+1)-1]/2. 这就是说 , 当 n=k+1 时 , k+1 条直线的 交点个数为 : f(k+1)=(k+1)[(k+1)-1]/2. 根据 (1) 、 (2) 可知 , 命题对一切大于 1 的正整数都成立 . 说明 : 用数学归纳法证明几何问题 , 重难点是处理好当 n=k+1 时利用假设结合几何知识证明命题成立 . 注 : 在上例的题设条件下还可以有如下二个结论 : (1) 设这 n 条直线互相分割成 f(n) 条线段或射线 , --- 则 : f(n)=n 2 . (2) 这 n 条直线把平面分成 (n 2 +n+2)/2 个区域 . 练习 1: 凸 n 边形有 f(n) 条对角线 , 则凸 n+1 边形的对角线 　　　　 ------ 的条数 f(n+1)=f(n)+_________. n-1 练习 2: 设有通过一点的 k 个平面 , 其中任何三个平面或 三个以上的平面不共有一条直线 , 这 k 个平面将 空间分成 f(k) 个区域 , 则 k+1 个平面将空间分成 f(k+1)=f(k)+__________ 个区域 . 2k １ : 平面内有 n 条直线 , 其中任何两条不平行 , 任何三条不过同一点 , 证明 这 n 条直线把平面分成 f(n) ＝ (n 2 +n+2)/2 个区域 . 作业： 再见