- 2021-06-22 发布 |
- 37.5 KB |
- 4页


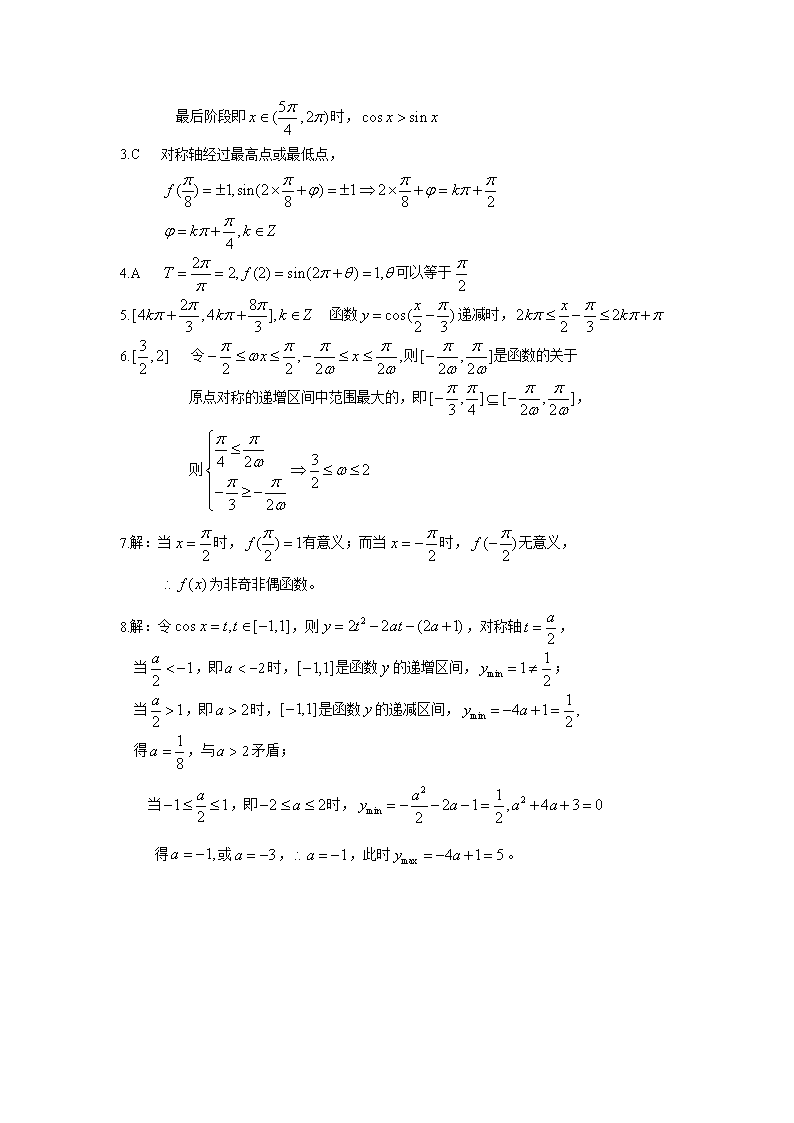
申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高三数学复习之30分钟小练习(22)
高三数学复习之30分钟小练习(22) 1.方程的解的个数是 A. B. C. D. 2.在内,使成立的取值范围为 A. B. C. D. 3.已知函数的图象关于直线对称,则可能是 A. B. C. D. 4.如果函数的最小正周期是,且当时取得最大值,那么 A. B. C. D. 5.函数的单调递增区间是___________________________. 6.设,若函数在上单调递增,则的取值范围是________。 7.判断函数的奇偶性。 8.设关于的函数的最小值为, 试确定满足的的值,并对此时的值求的最大值。 参考答案 1.C 在同一坐标系中分别作出函数的图象,左边三个交点, 右边三个交点,再加上原点,共计个 2.C 在同一坐标系中分别作出函数的图象,观察: 刚刚开始即时,; 到了中间即时,; 最后阶段即时, 3.C 对称轴经过最高点或最低点, 4.A 可以等于 5. 函数递减时, 6. 令则是函数的关于 原点对称的递增区间中范围最大的,即, 则 7.解:当时,有意义;而当时,无意义, 为非奇非偶函数。 8.解:令,则,对称轴, 当,即时,是函数的递增区间,; 当,即时,是函数的递减区间, 得,与矛盾; 当,即时, 得或,,此时。 天 星 教育网(www.tesoon.com) 版权所有 天 星 教育网(www.tesoon.com) 版权所有 天 星 教育网(www.tesoon.com) 版权所有 Tesoon.com 天 星版权 天·星om 权 天 星 教育网(www.tesoon.com) 版权所有 tesoon 天·星om 权 天·星om 权 Tesoon.com 天 星版权 tesoon tesoon tesoon 天 星查看更多