- 2021-06-21 发布 |
- 37.5 KB |
- 8页

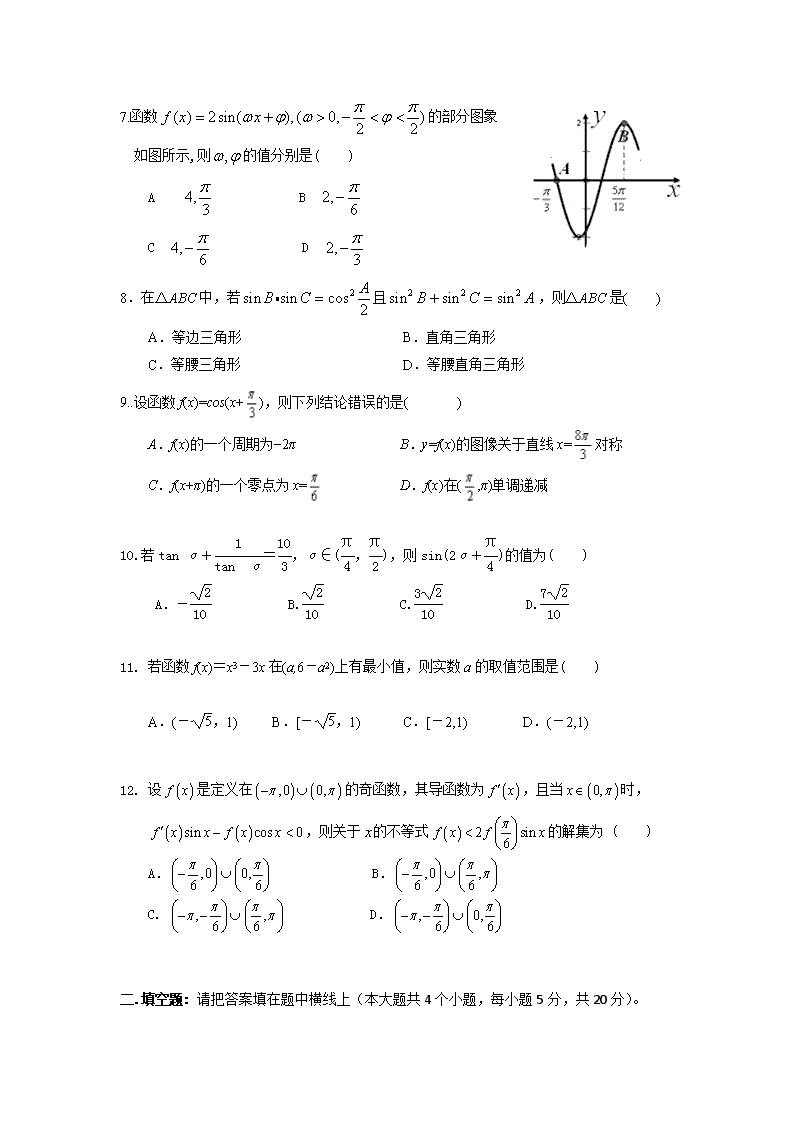

申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
数学理(普通班)卷·2018届福建省莆田第六中学高三10月月考(2017
2017-2018学年莆田六中高三10月份月考 数学理科B考试试卷 数学(集合与简易逻辑、函数与导数、三角函数与解三角形) 命题人:高三备课组 审核人:高三备课组 考试时间120分钟 满分150分 一、选择题(本大题共12小题,每小题5分,共60分。每小题有且只有一项是符合题目要求的) 1.已知集合A={1,3,},B={1,m},A∪B=A,则m等于( ). A.0或 B.0或3 C.1或 D.1或3或0 2. .等于( ) A.0 B. - C. - D.-1 3.若函数可导,则“有实根”是“有极值”的 ( ) A.必要不充分条件 B.充分不必要条件 C.充要条件 D.既不充分也不必要条件 4已知则的值为( ). A.1 B. 0 C. D. 5要得到函数的图象,只需将函数的图象( ) A.向左平移个单位 B.向右平移个单位 C.向左平移个单位 D.向右平移个单位 6. 已知,则的值为( ) A . B . C . D . 7.函数的部分图象 如图所示,则的值分别是( ) A B C D 8.在△ABC中,若且,则△ABC是( ) A.等边三角形 B.直角三角形 C.等腰三角形 D.等腰直角三角形 9..设函数f(x)=cos(x+),则下列结论错误的是( ) A.f(x)的一个周期为−2π B.y=f(x)的图像关于直线x=对称 C.f(x+π)的一个零点为x= D.f(x)在(,π)单调递减 10.若tan α+=,α∈(,),则sin(2α+)的值为( ) A.- B. C. D. 11. 若函数f(x)=x3-3x在(a,6-a2)上有最小值,则实数a的取值范围是( ) A.(-,1) B.[-,1) C.[-2,1) D.(-2,1) 12. 设是定义在的奇函数,其导函数为,且当时, ,则关于的不等式的解集为 ( ) A. B. C. D. 二.填空题: 请把答案填在题中横线上(本大题共4个小题,每小题5分,共20分)。 13. 函数的定义域____________. 14.在2012年7月12日伦敦奥运会上举行升旗 仪式.如图,在坡度为15°的观礼台上,某一列 座位所在直线AB与旗杆所在直线MN共面,在该 列的第一个座位A和最后一个座位B测得旗杆顶 端N的仰角分别为60°和30°,且座位A,B的距离 为10米,则旗杆的高度为________米. 15.已知关于x的方程2sin2x-sin 2x+m-1=0在上有两个不同的实数根,则m的 取值范围是________. 16. 若函数满足,对定义域内的任意恒成立, 则称为m函数,现给出下列函数: ①; ②; ③; ④ 其中为m函数的序号是_____________.(把你认为所有正确的序号都填上) 三、解答题:解答应写出文字说明、证明过程或演算步骤(本大题共6个大题,共70分) (温馨提示同学们做完选择题填空后做选做题 ) 17. (本小题满分12分).已知函数f(x)= (1)求函数f(x)的最小正周期和单调递增区间; (2)求函数f(x)在区间上的值域. 18(本小题满分12分).中,角,,的对边分别为,,,且. (1)求角的大小; (2)若为边上的中线,,,求的面积. 19(本小题满分12分).已知函数f(x)=(ax+b)lnx﹣bx+3在(1,f(1))处的 切线方程为y=2. (1)求a,b的值; (2)求函数f(x)的极值. (3)若g(x)=f(x)+kx在(1,3)是单调函数,求k的取值范围. 20、(本小题满分14分)、设函数. (1)求的单调区间; (2)当时,若方程在上有两个实数解,求实数t的取值范围; (3)证明:当m>n>0时,. (请考生注意在第(21),(22)二题都作答。) 21(本小题满分10分)选修4-4:坐标系与参数方程 在平面直角坐标系中,曲线C的参数方程为(α为参数).以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,直线l的极坐标方程为 .直线l与C交于A、B两点. (Ⅰ)求曲线C的普通方程及直线l的直角坐标方程; (Ⅱ)设点P(0,-2),求|PA|+|PB|的值. 22. (本小题满分10分)选修4-5 不等式选讲 已知关于x的不等式(其中)。 (Ⅰ)当时,求不等式的解集; (Ⅱ)若不等式有解,求实数的取值范围。 莆田六中2018届高三10月月考理科数学参考答案 一、选择题 1-5:BCABC 6-10:ADDDA 11-12:CB 二、填空题 13、,14、30 15、 16、②③ .三、解答题:解答应写出文字说明、证明过程或演算步骤(本大题共6个大题,共70分)。 17.. 解 (1)f(x)=cos+2sinsin =cos 2x+sin 2x+(sin x-cos x)(sin x+cos x) =cos 2x+sin 2x+sin2x-cos2x =cos 2x+sin 2x-cos 2x=sin................................... 4 ∴最小正周期T==π,..............................................................5 当,即时,函数单调递增, 所以函数的单调递增区间是,……… 7分 (2)∵x∈,∴2x-∈,.................................9 ∴-≤sin≤1................................................................11 即函数f(x)在区间上的值域为.......................12 18.解析:(1),由正弦定理,得, ∵,∴,...........3 ∴,∴ ∵,∴以,∴.又∵,∴..........6 (2)在中,由余弦定理得,∴ …①,.........................................8 在中,由正弦定理得,由已知得...............9 ∴,∴……②,........10 由①,②解得,.........11,∴.............12 19.解:(1)因为f(1)=(a+b)ln1﹣b+3=2,所以b=1;….......................1分 又f′(x)=+alnx+a﹣b=+alnx+a﹣1,…..............................................................2分 而函数f(x)=(ax+b)lnx﹣bx+3在(1,f(1))处的切线方程为y=2, 所以f′(1)=1+a﹣1=0,所以a=0;….....................................................3分 (2)由(1)得f(x)=lnx﹣x+3,f′(x)=﹣1,...............................4分 当0<x<1时,f′(x)>0;当x>1时,f′(x)<0; 所以f(x)在(0,1)上单调递增,f(x)在(1,+∞)上单调递减,…6分 所以f(x)有极大值f(1)=2,无极小值. 故f(x)的极大值为f(1)=2,无极小值; …........................................7分 (3)由g(x)=f(x)+kx,则g(x)=lnx+(k﹣1)x+3(x>0), ..............................................................................................8分 又由g(x)在x∈(1,3)上是单调函数,1)若g(x)为增函数时,有 所以有,,所以…..........................................10分 若g(x)为减函数时,有所以有, ,所以k≤0…................................................................................11分 故综上…................................................................12分 21.(Ⅰ) ①a=0时,f′(x)>0∴f(x)在(−1,+∞)上是增函数 …(1分) ②当a>0时,f(x)在上递增,在单调递减.…(4分) (Ⅱ)由(Ⅰ)知,f(x)在单调递增,在[0,1]上单调递减 又f(0)=0,f(1)=1−ln4, ∴当时,方程f(x)=t有两解 …(9分) (Ⅲ)要证:只需证 只需证:设,则 …(11分) 由(Ⅰ)知x−(1+x)ln(1+x),在(0,+∞)单调递减 …(12分) ∴x−(1+x)ln(1+x)<0,即g(x)是减函数,而m>n ∴g(m)查看更多
- 当前文档收益归属上传用户