数学卷·2018届湖北省荆州市沙市中学高二上学期期中数学试卷（理科） （解析版）

数学卷·2018届湖北省荆州市沙市中学高二上学期期中数学试卷（理科） （解析版）

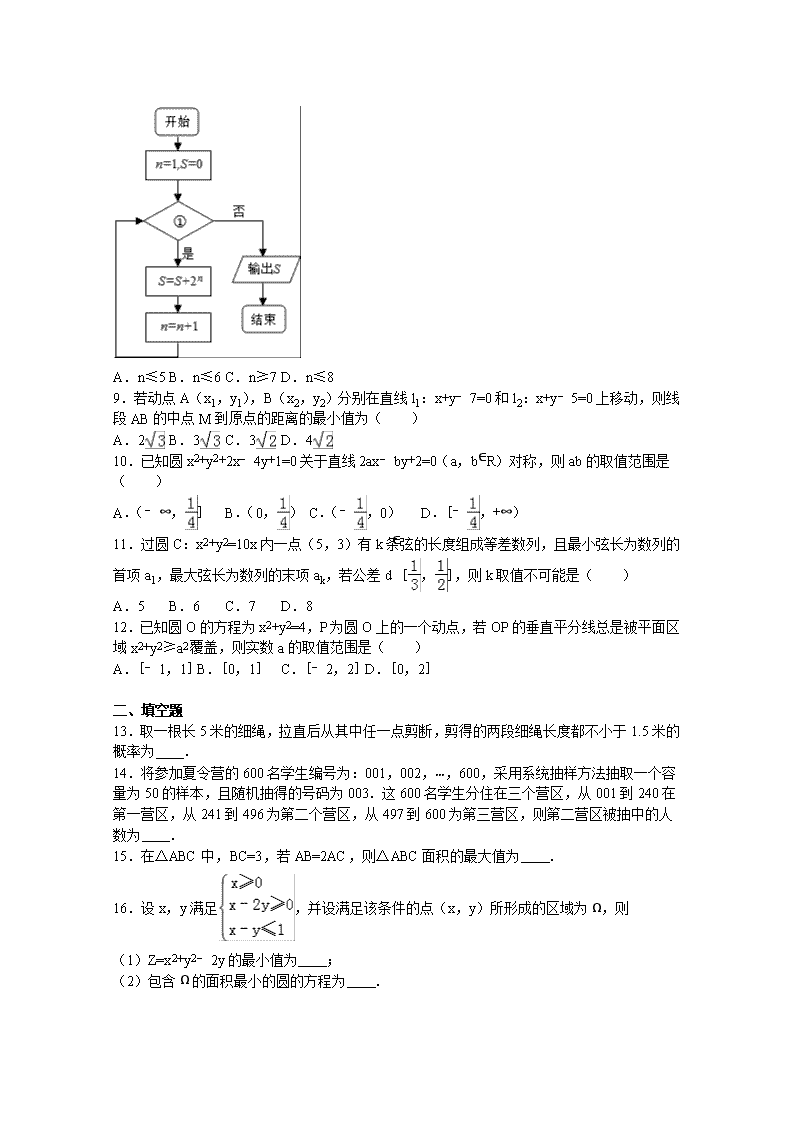
‎2016-2017学年湖北省荆州市沙市中学高二（上）期中数学试卷（理科）‎ ‎　‎ 一、选择题 ‎1．从分别写有A、B、C、D、E的5张卡片中，任取2张，这2张上的字母恰好按字母顺序相邻的概率为（　　）‎ A． B． C． D．‎ ‎2．已知倾斜角为α的直线l与直线x﹣2y+2=0平行，则tan2α的值为（　　）‎ A． B． C． D．‎ ‎3．总体由编号为01，02，…，19，20的20个个体组成．利用下面的随机数表选取5个个体，选取方法从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字，则选出来的第5个个体的编号为（　　）‎ ‎7816‎ ‎6572‎ ‎0802‎ ‎6314‎ ‎0702‎ ‎4369‎ ‎9728‎ ‎0198‎ ‎3204‎ ‎9234‎ ‎4935‎ ‎8200‎ ‎3623‎ ‎4869‎ ‎6938‎ ‎7481‎ A．08 B．07 C．02 D．01‎ ‎4．一条直线与平面所成的角为θ （0＜θ＜），则此直线与这个平面内任意一条直线所成角中最大角是（　　）‎ A． B．π C．π﹣θ D．θ ‎5．从装有2个红球和2个白球的口袋内任取2个球，那么互斥而不对立的两个事件是（　　）‎ A．至少有1个白球；都是白球 B．至少有1个白球；至少有1个红球 C．恰有1个白球；恰有2个白球 D．至少有一个白球；都是红球 ‎6．某学校课外活动兴趣小组对两个相关变量收集到5组数据如下表：‎ x ‎10‎ ‎20‎ ‎30‎ ‎40‎ ‎50‎ y ‎△‎ ‎68‎ ‎75‎ ‎81‎ ‎89‎ 由最小二乘法求得回归方程为，现发现表中有一个数据模糊不清，请推断该数据的值为 ‎（　　）‎ A．60 B．62 C．68 D．68.3‎ ‎7．两圆相交于点A（1，3）、B（m，﹣1），两圆的圆心均在直线x﹣y+c=0上，则m+c的值为（　　）‎ A．﹣1 B．2 C．3 D．0‎ ‎8．阅读如图所示的程序框图，若输出的S是126，则①处应填（　　）‎ A．n≤5 B．n≤6 C．n≥7 D．n≤8‎ ‎9．若动点A（x1，y1），B（x2，y2）分别在直线l1：x+y﹣7=0和l2：x+y﹣5=0上移动，则线段AB的中点M到原点的距离的最小值为（　　）‎ A．2 B．3 C．3 D．4‎ ‎10．已知圆x2+y2+2x﹣4y+1=0关于直线2ax﹣by+2=0（a，b∈R）对称，则ab的取值范围是（　　）‎ A．（﹣∞，] B．（0，） C．（﹣，0） D．[﹣，+∞）‎ ‎11．过圆C：x2+y2=10x内一点（5，3）有k条弦的长度组成等差数列，且最小弦长为数列的首项a1，最大弦长为数列的末项ak，若公差d∈[，]，则k取值不可能是（　　）‎ A．5 B．6 C．7 D．8‎ ‎12．已知圆O的方程为x2+y2=4，P为圆O上的一个动点，若OP的垂直平分线总是被平面区域x2+y2≥a2覆盖，则实数a的取值范围是（　　）‎ A．[﹣1，1] B．[0，1] C．[﹣2，2] D．[0，2]‎ ‎　‎ 二、填空题 ‎13．取一根长5米的细绳，拉直后从其中任一点剪断，剪得的两段细绳长度都不小于1.5米的概率为　　．‎ ‎14．将参加夏令营的600名学生编号为：001，002，…，600，采用系统抽样方法抽取一个容量为50的样本，且随机抽得的号码为003．这600名学生分住在三个营区，从001到240在第一营区，从241到496为第二个营区，从497到600为第三营区，则第二营区被抽中的人数为　　．‎ ‎15．在△ABC中，BC=3，若AB=2AC，则△ABC面积的最大值为　　．‎ ‎16．设x，y满足，并设满足该条件的点（x，y）所形成的区域为Ω，则 ‎（1）Z=x2+y2﹣2y的最小值为　　；‎ ‎（2）包含Ω的面积最小的圆的方程为　　．‎ ‎　‎ 三、解答题 ‎17．已知两条直线l1：x+（1+m）y=2﹣m，l2：2mx+4y=﹣16，m为何值时，l1与l2：（1）平行 （2）垂直．‎ ‎18．已知圆O：x2+y2=8内有一点P0（﹣1，2），AB为过点P0且倾斜角为α的弦．‎ ‎（1）当α=45°时，求AB的长；‎ ‎（2）当弦AB被点P0平分时，求直线AB的方程．‎ ‎19．某市统计局就某地居民的月收入调查了10000人，并根据所得数据画出样本的频率分布直方图如图所示．（每个分组包括左端点，不包括右端点，如第一组表示[1000，1500）．‎ ‎（1）求居民收入在[2000，3000）的频率；‎ ‎（2）根据频率分布直方图算出样本数据的中位数；‎ ‎（3）为了分析居民的收入与年龄、职业等方面的关系，必须按月收入再从这10 000人中按分层抽样方法抽出100人作进一步分析，则月收入在[2000，3000）的这段应抽取多少人？‎ ‎20．已知关于x的一元二次函数f（x）=ax2﹣4bx+1．‎ ‎（1）设集合P={1，2，3}和Q={﹣1，1，2，3，4}，分别从集合P和Q中随机取一个数作为a和b，求函数y=f（x）在区间[1，+∞）上是增函数的概率；‎ ‎（2）设点（a，b）是区域内的随机点，求y=f（x）在区间[1，+∞）上是增函数的概率．‎ ‎21．如图，已知平面ABB1N⊥平面BB1C1C，四边形BB1C1C是矩形，ABB1N是梯形，且AN⊥AB，AN∥BB1，AB=BC=AN=4，BB1=8．‎ ‎（1）求证：BN⊥平面C1B1N；‎ ‎（2）求直线NC和平面NB1C1所成角的正弦值；‎ ‎（3）若M为AB中点，在BC边上找一点P，使MP∥平面CNB1，并求的值．‎ ‎22．已知点H在圆D：（x﹣2）2+（y+3）2=32上运动，点P的坐标为（﹣6，3），线段PH的中点为M．‎ ‎（1）求点M的轨迹方程；‎ ‎（2）平面内是否存在定点A（a，b）（a≠0），使|MO|=λ|MA|（λ≠1常数），若存在，求出A的坐标及λ的值；若不存在，说明理由；‎ ‎（3）若直线y=kx与M的轨迹交于B、C两点，点N（0，t）使NB⊥NC，求实数t的范围．‎ ‎　‎ ‎2016-2017学年湖北省荆州市沙市中学高二（上）期中数学试卷（理科）‎ 参考答案与试题解析 ‎　‎ 一、选择题 ‎1．从分别写有A、B、C、D、E的5张卡片中，任取2张，这2张上的字母恰好按字母顺序相邻的概率为（　　）‎ A． B． C． D．‎ ‎【考点】等可能事件的概率．‎ ‎【分析】由题意知本题是一个古典概型，试验包含的总事件是从5张卡片中任取2张，有C52种取法，这2张上的字母恰好按字母顺序相邻的有A，B；B，C；C，D；D，E四种结果，代入公式，得到结果．‎ ‎【解答】解：由题意知本题是一个古典概型，‎ ‎∵试验包含的总事件是从5张卡片中任取2张，有C52中取法，‎ 这2张上的字母恰好按字母顺序相邻的有A，B；B，C；C，D；D，E四种结果，‎ ‎∴由古典概型公式得到 P==．‎ 故选B．‎ ‎　‎ ‎2．已知倾斜角为α的直线l与直线x﹣2y+2=0平行，则tan2α的值为（　　）‎ A． B． C． D．‎ ‎【考点】二倍角的正切；直线的倾斜角．‎ ‎【分析】由题意可得tanα=，代入二倍角公式tan2α=可求 ‎【解答】解：由题意可得tanα=‎ ‎∴tan2α===‎ 故选C ‎　‎ ‎3．总体由编号为01，02，…，19，20的20个个体组成．利用下面的随机数表选取5个个体，选取方法从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字，则选出来的第5个个体的编号为（　　）‎ ‎7816‎ ‎6572‎ ‎0802‎ ‎6314‎ ‎0702‎ ‎4369‎ ‎9728‎ ‎0198‎ ‎3204‎ ‎9234‎ ‎4935‎ ‎8200‎ ‎3623‎ ‎4869‎ ‎6938‎ ‎7481‎ A．08 B．07 C．02 D．01‎ ‎【考点】简单随机抽样．‎ ‎【分析】从随机数表第1行的第5列和第6列数字开始由左到右一次选取两个数字开始向右读，依次为65，72，08，02，63，14，07，02，43，69，97，28，01，98，…，其中08，02，14，07，01符合条件，故可得结论．‎ ‎【解答】解：从随机数表第1行的第5列和第6列数字开始由左到右一次选取两个数字开始向右读，‎ 第一个数为65，不符合条件，第二个数为72，不符合条件，‎ 第三个数为08，符合条件，‎ 以下符合条件依次为：08，02，14，07，01，‎ 故第5个数为01．‎ 故选：D．‎ ‎　‎ ‎4．一条直线与平面所成的角为θ （0＜θ＜），则此直线与这个平面内任意一条直线所成角中最大角是（　　）‎ A． B．π C．π﹣θ D．θ ‎【考点】直线与平面所成的角．‎ ‎【分析】一条直线与平面所成的角为θ，根据线面夹角的性质即最小角定理，我们可以求出这条直线与这个平面内任意一直线所成角的范围，进而求出其最大值，得到正确选项．‎ ‎【解答】证明：已知AB是平面a的斜线，A是斜足，BC⊥平面a，C为垂足，‎ 则直线AC是斜线AB在平面a内的射影．‎ 设AD是平面a内的任一条直线，且BD⊥AD，垂足为D，‎ 又设AB与AD所成的角∠BAD，AB与AC所成的角为∠BAC．‎ BC⊥平面a mBD⊥AD 由三垂线定理可得：DC⊥AC sin∠BAD=，sin∠BAC=‎ 在Rt△BCD中，BD＞BC，‎ ‎∠BAC，∠BAD是Rt△内的一个锐角所以∠BAC＜∠BAD．‎ 从上面的证明过程我们可以得到最小角定理：斜线和平面所成角是这条斜线和平面内经过斜足的直线所成的一切角中最小的角 这条斜线和平面内经过斜足的直线所成的一切角中最大的角为90°，‎ 由已知中直线与一个平面成θ角，‎ 则这条直线与这个平面内不经过斜足的直线所成角的为范围（θ≤r≤）‎ 故选A．‎ ‎　‎ ‎5．从装有2个红球和2个白球的口袋内任取2个球，那么互斥而不对立的两个事件是（　　）‎ A．至少有1个白球；都是白球 B．至少有1个白球；至少有1个红球 C．恰有1个白球；恰有2个白球 D．至少有一个白球；都是红球 ‎【考点】互斥事件与对立事件．‎ ‎【分析】由题意知所有的实验结果为：“都是白球”，“1个白球，1个红球”，“都是红球”，再根据互斥事件的定义判断．‎ ‎【解答】解：A、“至少有1个白球”包含“1个白球，1个红球”和“都是白球”，故A不对；‎ B、“至少有1个红球”包含“1个白球，1个红球”和“都是红球”，故B不对；‎ C、“恰有1个白球”发生时，“恰有2个白球”不会发生，且在一次实验中不可能必有一个发生，故C对；‎ D、“至少有1个白球”包含“1个白球，1个红球”和“都是白球”，与都是红球，是对立事件，故D不对；‎ 故选C．‎ ‎　‎ ‎6．某学校课外活动兴趣小组对两个相关变量收集到5组数据如下表：‎ x ‎10‎ ‎20‎ ‎30‎ ‎40‎ ‎50‎ y ‎△‎ ‎68‎ ‎75‎ ‎81‎ ‎89‎ 由最小二乘法求得回归方程为，现发现表中有一个数据模糊不清，请推断该数据的值为 ‎（　　）‎ A．60 B．62 C．68 D．68.3‎ ‎【考点】线性回归方程．‎ ‎【分析】由题意设要求的数据为t，由于回归直线过样本点的中心，分别求得和，代入回归方程可得t的值．‎ ‎【解答】解：由题意可得=（10+20+30+40+50）=30，‎ 设要求的数据为t，则有=（t+68+75+81+89）=（t+303），‎ 因为回归直线过样本点的中心．‎ 所以（t+303）=0.67×30+54.9，解得t=62．‎ 故选B．‎ ‎　‎ ‎7．两圆相交于点A（1，3）、B（m，﹣1），两圆的圆心均在直线x﹣y+c=0上，则m+c的值为（　　）‎ A．﹣1 B．2 C．3 D．0‎ ‎【考点】圆与圆的位置关系及其判定．‎ ‎【分析】根据题意可知，x﹣y+c=0是线段AB的垂直平分线，由垂直得到斜率乘积为﹣1，而直线x﹣y+c=0的斜率为1，所以得到过A和B的直线斜率为1，利用A和B的坐标表示出直线AB的斜率等于1，列出关于m的方程，求出方程的解即可得到m的值，然后利用中点公式和m的值求出线段AB的中点坐标，把中点坐标代入x﹣y+c=0中即可求出c的值，利用m和c的值求出m+c的值即可．‎ ‎【解答】解：由题意可知：直线x﹣y+c=0是线段AB的垂直平分线，又直线x﹣y+c=0 的斜率为1，‎ 则=﹣1①，且﹣+c=0②，‎ 由①解得m=5，把m=5代入②解得c=﹣2，则m+c=5﹣2=3．‎ 故选C ‎　‎ ‎8．阅读如图所示的程序框图，若输出的S是126，则①处应填（　　）‎ A．n≤5 B．n≤6 C．n≥7 D．n≤8‎ ‎【考点】程序框图．‎ ‎【分析】分析程序中各变量、各语句的作用，再根据流程图所示的顺序，可知：该程序的作用是累加并输出变量S的值，要确定进行循环的条件，可模拟程序的运行，对每次循环中各变量的值进行分析，不难得到题目要求的结果 ‎【解答】解：第一次循环，s=0+21=2，n=1+1=2，进入下一次循环；‎ 第二次循环，s=2+22=6，n=2+1=3，进入下一次循环；‎ 第三次循环，s=6+23=14，n=3+1=4，进入下一次循环；‎ 第四次循环，s=14+24=30，n=4+1=5，进入下一次循环；‎ 第五次循环，s=30+25=62，n=5+1=6，进入下一次循环；‎ 第六次循环，s=62+26=126，n=6+1=7，循环结束，即判断框中的条件不成立了，所以框中的条件应该是n≤6，‎ 故选：B．‎ ‎　‎ ‎9．若动点A（x1，y1），B（x2，y2）分别在直线l1：x+y﹣7=0和l2：x+y﹣5=0上移动，则线段AB的中点M到原点的距离的最小值为（　　）‎ A．2 B．3 C．3 D．4‎ ‎【考点】两点间的距离公式；中点坐标公式．‎ ‎【分析】根据题意可推断出M点的轨迹为平行于直线l1、l2且到l1、l2距离相等的直线l进而根据两直线方程求得M的轨迹方程，进而利用点到直线的距离求得原点到直线的距离为线段AB的中点M到原点的距离的最小值为，求得答案．‎ ‎【解答】解：由题意知，M点的轨迹为平行于直线l1、l2且到l1、l2距离相等的直线l，故其方程为x+y﹣6=0，‎ ‎∴M到原点的距离的最小值为d==3．‎ 故选C ‎　‎ ‎10．已知圆x2+y2+2x﹣4y+1=0关于直线2ax﹣by+2=0（a，b∈R）对称，则ab的取值范围是（　　）‎ A．（﹣∞，] B．（0，） C．（﹣，0） D．[﹣，+∞）‎ ‎【考点】圆的一般方程．‎ ‎【分析】把圆的方程化为标准方程，找出圆心坐标和半径，由已知圆关于直线2ax﹣by+2=0对称，得到圆心在直线上，故把圆心坐标代入已知直线方程得到a与b的关系式，由a表示出b，设m=ab，将表示出的b代入ab中，得到m关于a的二次函数关系式，由二次函数求最大值的方法即可求出m的最大值，即为ab的最大值，即可写出ab的取值范围．‎ ‎【解答】解：把圆的方程化为标准方程得：（x+1）2+（y﹣2）2=4，‎ ‎∴圆心坐标为（﹣1，2），半径r=2，‎ 根据题意可知：圆心在已知直线2ax﹣by+2=0上，‎ 把圆心坐标代入直线方程得：﹣2a﹣2b+2=0，即b=1﹣a，‎ 则设m=ab=a（1﹣a）=﹣a2+a，‎ ‎∴当a=时，m有最大值，最大值为，即ab的最大值为，‎ 则ab的取值范围是（﹣∞，]．‎ 故选：A．‎ ‎　‎ ‎11．过圆C：x2+y2=10x内一点（5，3）有k条弦的长度组成等差数列，且最小弦长为数列的首项a1，最大弦长为数列的末项ak，若公差d∈[，]，则k取值不可能是（　　）‎ A．5 B．6 C．7 D．8‎ ‎【考点】直线与圆的位置关系．‎ ‎【分析】根据题意可知，最短弦为垂直OA的弦，a1=8，最长弦为直径：aK=10，由等差数列的性质可以求出公差d的取值范围．‎ ‎【解答】解：设A（5，3），圆心O（5，0），‎ 最短弦为垂直OA的弦，a1=8，最长弦为直径：aK=10，‎ 公差d=，‎ ‎∴，‎ ‎∴5≤k≤7‎ 故选：D．‎ ‎　‎ ‎12．已知圆O的方程为x2+y2=4，P为圆O上的一个动点，若OP的垂直平分线总是被平面区域x2+y2≥a2覆盖，则实数a的取值范围是（　　）‎ A．[﹣1，1] B．[0，1] C．[﹣2，2] D．[0，2]‎ ‎【考点】几何概型．‎ ‎【分析】随着点P在圆上运动，OP的垂直平分线形成的区域是圆：x2+y2=1的外部，再结合题意分析这两个区域的相互覆盖情况即可．‎ ‎【解答】解：随着点P在圆上运动，OP的垂直平分线形成的区域是圆：x2+y2=1的外部，…①‎ 平面区域x2+y2≥a2表示以原点为圆心，a为半径的圆的外部，…②‎ 若OP的垂直平分线总是被平面区域x2+y2≥a2覆盖，‎ 则①区域要包含②区域，‎ 故|a|≤1，∴﹣1≤a≤1．‎ 故选A．‎ ‎　‎ 二、填空题 ‎13．取一根长5米的细绳，拉直后从其中任一点剪断，剪得的两段细绳长度都不小于1.5米的概率为　　．‎ ‎【考点】几何概型．‎ ‎【分析】根据题意确定为几何概型中的长度类型，将长度为5m的绳子分成相等的三段，在中间一段任意位置剪断符合要求，从而找出中间2m处的两个界点，再求出其比值．‎ ‎【解答】解：记“两段的长都不小于1.5米”为事件A，‎ 则只能在距离两段超过1.5米的绳子上剪断，‎ 即在中间的2米的绳子上剪断，才使得剪得两段的长都不小于1.5米，‎ 所以由几何概型的公式得到事件A发生的概率 P（A）=．‎ 故答案为．‎ ‎　‎ ‎14．将参加夏令营的600名学生编号为：001，002，…，600，采用系统抽样方法抽取一个容量为50的样本，且随机抽得的号码为003．这600名学生分住在三个营区，从001到240在第一营区，从241到496为第二个营区，从497到600为第三营区，则第二营区被抽中的人数为　18　．‎ ‎【考点】系统抽样方法．‎ ‎【分析】由于是系统抽样，故先随机抽取第一数，再确定间隔，可知样本组成以3为首项，12为公差的等差数列，由此可得结论．‎ ‎【解答】解：由题意，在随机抽样中，首次抽到003号，‎ 以后每隔12个号抽到一个人，‎ 则分别是003、015、027、039构成以3为首项，12为公差的等差数列，通项为12n﹣9，‎ 由241≤12n﹣9≤496，∴25≤n≤46‎ ‎∴第二营区被抽中的人数为46﹣25+1=18．‎ 故答案为18．‎ ‎　‎ ‎15．在△ABC中，BC=3，若AB=2AC，则△ABC面积的最大值为　3　．‎ ‎【考点】正弦定理．‎ ‎【分析】设AC=x，则AB=2x，根据面积公式得S△ABC=x，由余弦定理求得 cosC代入化简 S△ABC=，由三角形三边关系求得 1＜x＜3，由二次函数的性质求得S△ABC取得最大值．‎ ‎【解答】解：设AC=x，则AB=2x，根据面积公式得S△ABC=AC•BC•sinC=x•sinC=x．‎ 由余弦定理可得 cosC=，‎ ‎∴S△ABC=x=x =．‎ 由三角形三边关系有：x+2x＞3且x+3＞2x，解得 1＜x＜3，‎ 故当 x=时，S△ABC取得最大值3，‎ 故答案为：3．‎ ‎　‎ ‎16．设x，y满足，并设满足该条件的点（x，y）所形成的区域为Ω，则 ‎（1）Z=x2+y2﹣2y的最小值为　　；‎ ‎（2）包含Ω的面积最小的圆的方程为　x2+y2﹣3x+y=0　．‎ ‎【考点】二元一次不等式（组）与平面区域．‎ ‎【分析】作出不等式组对应的平面区域，利用目标函数的几何意义，利用数形结合进行求解即可．‎ ‎【解答】解：x，y满足的平面区域如图：‎ ‎（1）Z=x2+y2﹣2y=x2+（y﹣1）2﹣1的最小值为（0，1）到直线x﹣2y=0的距离的平方减去1，为||2﹣1=﹣；‎ ‎（2）包含Ω的面积最小的圆的方程即为三角形区域的外接圆方程，则此时过点O，‎ B（2，1），A（0，﹣1）三点的圆，‎ 设圆的一般方程为x2+y2+Dx+Ey+F=0，得到，解得，‎ 所以包含Ω的面积最小的圆的方程为 x2+y2﹣3x+y=0．‎ 故答案为：；x2+y2﹣3x+y=0．‎ ‎　‎ 三、解答题 ‎17．已知两条直线l1：x+（1+m）y=2﹣m，l2：2mx+4y=﹣16，m为何值时，l1与l2：（1）平行 （2）垂直．‎ ‎【考点】直线的一般式方程与直线的平行关系；直线的一般式方程与直线的垂直关系．‎ ‎【分析】（1）解1×4﹣（1+m）（2m）=0，排除两直线重合即可；（2）由垂直关系可得1×2m+4（1+m）=0，解方程可得．‎ ‎【解答】解：（1）∵l1：x+（1+m）y=2﹣m，l2：2mx+4y=﹣16，‎ ‎∴1×4﹣（1+m）（2m）=0，解得m=1或m=﹣2，‎ 当m=﹣2时，两直线重合，当m=1时两直线平行；‎ ‎（2）由垂直关系可得1×2m+4（1+m）=0，‎ 解得m=，‎ ‎∴当m=时，两直线垂直．‎ ‎　‎ ‎18．已知圆O：x2+y2=8内有一点P0（﹣1，2），AB为过点P0且倾斜角为α的弦．‎ ‎（1）当α=45°时，求AB的长；‎ ‎（2）当弦AB被点P0平分时，求直线AB的方程．‎ ‎【考点】直线与圆的位置关系．‎ ‎【分析】（1）依题意直线AB的斜率为1，直线AB的方程，根据圆心0（0，0）到直线AB的距离，由弦长公式求得AB的长．‎ ‎（2）当弦AB被点P0平分时，AB和OP0垂直，故AB 的斜率为，根据点斜式方程直线AB的方程．‎ ‎【解答】解：（1）依题意直线AB的斜率为1，直线AB的方程为：y﹣2=x+1，即x﹣y+3=0，‎ 圆心0（0，0）到直线AB的距离为d=，则AB的长为2=．‎ ‎（2）当弦AB被点P0平分时，AB和OP0垂直，故AB 的斜率为，根据点斜式方程直线AB的方程为x﹣2y+5=0．‎ ‎　‎ ‎19．某市统计局就某地居民的月收入调查了10000人，并根据所得数据画出样本的频率分布直方图如图所示．（每个分组包括左端点，不包括右端点，如第一组表示[1000，1500）．‎ ‎（1）求居民收入在[2000，3000）的频率；‎ ‎（2）根据频率分布直方图算出样本数据的中位数；‎ ‎（3）为了分析居民的收入与年龄、职业等方面的关系，必须按月收入再从这10 000人中按分层抽样方法抽出100人作进一步分析，则月收入在[2000，3000）的这段应抽取多少人？‎ ‎【考点】分层抽样方法；频率分布直方图．‎ ‎【分析】（1）根据频率=小矩形的高×组距来求；‎ ‎（2）根据中位数的左右两边的矩形的面积和相等，所以只需求出从左开始面积和等于0.5的底边横坐标的值即可，运用取中间数乘频率，再求之和，计算可得平均数；‎ ‎（3）求出月收入在[2000，3000）的人数，用分层抽样的抽取比例乘以人数，可得答案．‎ ‎【解答】解：（Ⅰ）月收入在[2000，3000）的频率为：‎ ‎0.0005×=0.5；　 3分 ‎（Ⅱ）∵0.0002×=0.1，‎ ‎0.0004×=0.2，‎ ‎0.0005×=0.25，‎ ‎0.1+0.2+0.25=0.55＞0.5，‎ 所以，样本数据的中位数为：‎ ‎2000+=2000+400=2400（元） 7分 ‎（Ⅲ）居民月收入在[2000，3000）的频数为0.5×10000=5000（人），‎ 再从10000人中用分层抽样方法抽出100人，‎ 则月收入在[2500，3000）的这段应抽取100×=50（人）‎ ‎　‎ ‎20．已知关于x的一元二次函数f（x）=ax2﹣4bx+1．‎ ‎（1）设集合P={1，2，3}和Q={﹣1，1，2，3，4}，分别从集合P和Q中随机取一个数作为a和b，求函数y=f（x）在区间[1，+∞）上是增函数的概率；‎ ‎（2）设点（a，b）是区域内的随机点，求y=f（x）在区间[1，+∞）上是增函数的概率．‎ ‎【考点】等可能事件的概率．‎ ‎【分析】（1）本题是一个等可能事件的概率，试验发生包含的事件是3×5，满足条件的事件是函数f（x）=ax2﹣4bx+1在区间[1，+∞）上为增函数，根据二次函数的对称轴，写出满足条件的结果，得到概率．‎ ‎（2）本题是一个等可能事件的概率问题，根据第一问做出的函数是增函数，得到试验发生包含的事件对应的区域和满足条件的事件对应的区域，做出面积，得到结果．‎ ‎【解答】解：（1）由题意知本题是一个等可能事件的概率，‎ ‎∵试验发生包含的事件是3×5=15，‎ 函数f（x）=ax2﹣4bx+1的图象的对称轴为，‎ 要使f（x）=ax2﹣4bx+1在区间[1，+∞）上为增函数，‎ 当且仅当a＞0且，即2b≤a 若a=1则b=﹣1，若a=2则b=﹣1，1；若a=3则b=﹣1，1；‎ ‎∴事件包含基本事件的个数是1+2+2=5‎ ‎∴所求事件的概率为．‎ ‎（2）由（Ⅰ）知当且仅当2b≤a且a＞0时，‎ 函数f（x）=ax2﹣4bx+1在区是间[1，+∞）上为增函数，‎ 依条件可知试验的全部结果所构成的区域为 构成所求事件的区域为三角形部分 由得交点坐标为，‎ ‎∴所求事件的概率为．‎ ‎　‎ ‎21．如图，已知平面ABB1N⊥平面BB1C1C，四边形BB1C1C是矩形，ABB1N是梯形，且AN⊥AB，AN∥BB1，AB=BC=AN=4，BB1=8．‎ ‎（1）求证：BN⊥平面C1B1N；‎ ‎（2）求直线NC和平面NB1C1所成角的正弦值；‎ ‎（3）若M为AB中点，在BC边上找一点P，使MP∥平面CNB1，并求的值．‎ ‎【考点】直线与平面平行的性质；直线与平面垂直的判定．‎ ‎【分析】（1）BA，BC，BB1两两垂直． 以B为坐标原点，分别以BA，BC，BB1所在直线别为x，y，z轴建立空间直角坐标系，证出BN⊥NB1，BN⊥B1C1后即可证明BN⊥平面C1B1N；‎ ‎（2）求出平面NCB1的一个法向量，利用与此法向量的夹角求出直线NC和平面NB1C1所成角的正弦值；（3）设P（0，0，a）为BC上一点，由MP∥平面CNB1，得知=0，利用向量数量积为0求出a的值，并求出的值．‎ ‎【解答】（1）证明：∵BA，BC，BB1两两垂直． …‎ 以B为坐标原点，分别以BA，BC，BB1所在直线别为x，y，z轴建立空间直角坐标系，‎ 则N（4，4，0），B1（0，8，0），C1（0，8，4），C（0，0，4）‎ ‎∵=（4，4，0）•（﹣4，4，0）=﹣16+16=0‎ ‎=（4，4，0）•（0，0，4）=0‎ ‎∴BN⊥NB1，BN⊥B1C1且NB1与B1C1相交于B1，‎ ‎∴BN⊥平面C1B1N； …‎ ‎（2）解：设=（x，y，z）为平面NB1C1的一个法向量，‎ 则，取=（1，1，0），‎ ‎∵=（4，4，﹣4），‎ ‎∴直线NC和平面NB1C1所成角的正弦值sinθ==；…‎ ‎（3）解：∵M（2，0，0）．设P（0，0，a）为BC上一点，则=（﹣2，0，a），‎ ‎∵MP∥平面CNB1，‎ ‎∴=0，‎ ‎∴（﹣2，0，a）•（1，1，2）=0，‎ ‎∴a=1．‎ 又PM⊄平面CNB1，∴MP∥平面CNB1，‎ ‎∴当PB=1时，MP∥平面CNB1‎ ‎∴=…‎ ‎　‎ ‎22．已知点H在圆D：（x﹣2）2+（y+3）2=32上运动，点P的坐标为（﹣6，3），线段PH的中点为M．‎ ‎（1）求点M的轨迹方程；‎ ‎（2）平面内是否存在定点A（a，b）（a≠0），使|MO|=λ|MA|（λ≠1常数），若存在，求出A的坐标及λ的值；若不存在，说明理由；‎ ‎（3）若直线y=kx与M的轨迹交于B、C两点，点N（0，t）使NB⊥NC，求实数t的范围．‎ ‎【考点】轨迹方程．‎ ‎【分析】（1）利用代入法求点M的轨迹方程；‎ ‎（2）求出λ2==，可得结论；‎ ‎（3）利用韦达定理及向量垂直的结论，即可求t的范围．‎ ‎【解答】解：（1）设点M（x，y），则H（2x+6，2y﹣3），‎ 又H在圆上，得（2x+6﹣2）2+（2y﹣3+3）2=32，化简得（x+2）2+y2=8；‎ ‎（2）设M的轨迹交y轴于E、F，由且|EO|=|FO|知，|EA|=|FA|，‎ 所以A在x轴上，设M（x，y），‎ 则λ2==，‎ 所以4+a2=2a+4，a=2或0（舍），即A（2，0），；‎ ‎（3）由直线y=kx与（x+2）2+y2=8，消去y得（1+k2）x2+4x﹣4=0，‎ ‎∴x1+x2=x1x2=﹣，‎ 又 0==（1+k2）x1x2﹣kt（x1+x2）+t2，‎ ‎∴=∈[﹣，]，‎ ‎∴t．‎ ‎　‎