2017-2018学年福建省莆田第八中学高二下学期期中考试数学（理）试题 Word版

2017-2018学年福建省莆田第八中学高二下学期期中考试数学（理）试题 Word版

‎2017-2018学年福建省莆田第八中学高二下学期期中考试数学理试卷 班级： 座号： 姓名： 命题人：徐强 审题人：吴元良 一、选择题(12小题，每小题5分,共60分)‎ ‎1．复数的实部是( )‎ A．－2 B．‎2 C．3 D．4‎ ‎2．张、王两家夫妇各带1个小孩一起到动物园游玩，购票后排队依次入园．为安全起见，首尾一定要排两位爸爸，另外，两个小孩一定要排在一起，则这6人的入园顺序排法种数共有(　　)‎ A．12 B．‎24 C．36 D．48‎ ‎3．下列说法正确的是　(　　)‎ A.命题“若x2=1,则x=‎1”‎的否命题为“若x2=1,则x≠‎‎1”‎ B.命题“∀x≥0,x2+x-1<‎0”‎的否定是“∃x0<0,+x0-1<‎‎0”‎ C.命题“若x=y,则sinx=siny”的逆否命题为假命题 D.若“p∨q”为真命题,则p,q中至少有一个为真命题 ‎4.的展开式中的常数项为　(　　)‎ A.12 B.‎-12 ‎ C.6 D.-6‎ ‎5.使不等式x2-3x<0成立的一个必要不充分条件是　(　　)‎ A.03‎ ‎6．已知，，是空间的一个基底，设＝＋，＝－，则下列向量中可以与，一起构成空间的另一个基底的是(　　)‎ A． B． C． D．以上都不对 ‎7.如图1，已知F是椭圆＋＝1(a>b>0)的左焦点，P是椭圆上的一点，PF⊥x轴，OP∥AB(O为原点)，则该椭圆的离心率是(　　)‎ 图1‎ A. B． C． D． ‎8. 定积分的值为（ ）‎ A. 0 B. C. 2 D. 4‎ ‎9. 若函数的图象上存在两点，使得函数的图象在这两点处的切线互相垂直，则称具有T性质，下列函数中具有T性质的是（ ）‎ A. B. C. D. ‎ ‎10.若直线y=kx-2与抛物线y2=8x交于A,B两个不同的点,且AB的中点的横坐标为2,则k等于　(　　)‎ A.2或-1 B.‎-1 C.2 D.1± ‎11．设f(x)，g(x)分别是定义在R上的奇函数和偶函数，当x＜0时，f′(x)g(x)－f(x)g′(x)>0，且f(3)＝0，则不等式f(x)g(x)<0的解集是(　　)‎ A．(－3,0)∪(3，＋∞) B．(－3,0)∪(0,3)‎ C．(－∞，－3)∪(3，＋∞) D．(－∞，－3)∪(0,3)‎ ‎12. 已知是平面的斜线段，为斜足，若与平面成角，过定点的动直线与斜线 成角，且交于点，则动点的轨迹是( )‎ A. 圆 B. 椭圆 C.双曲线 D.抛物线 二、填空题(4小题，每小题5分，共20分)‎ ‎13、双曲线－＝1的渐近线的方程为________．‎ ‎14.已知随机变量服从正态分布， ，则＝__________‎ ‎15．若三角形内切圆的半径为，三边长为，则三角形的面积等于，根据类比推理的方法，若一个四面体的内切球的半径为，四个面的面积分别是，则四面体的体积　　　　　．‎ ‎16. 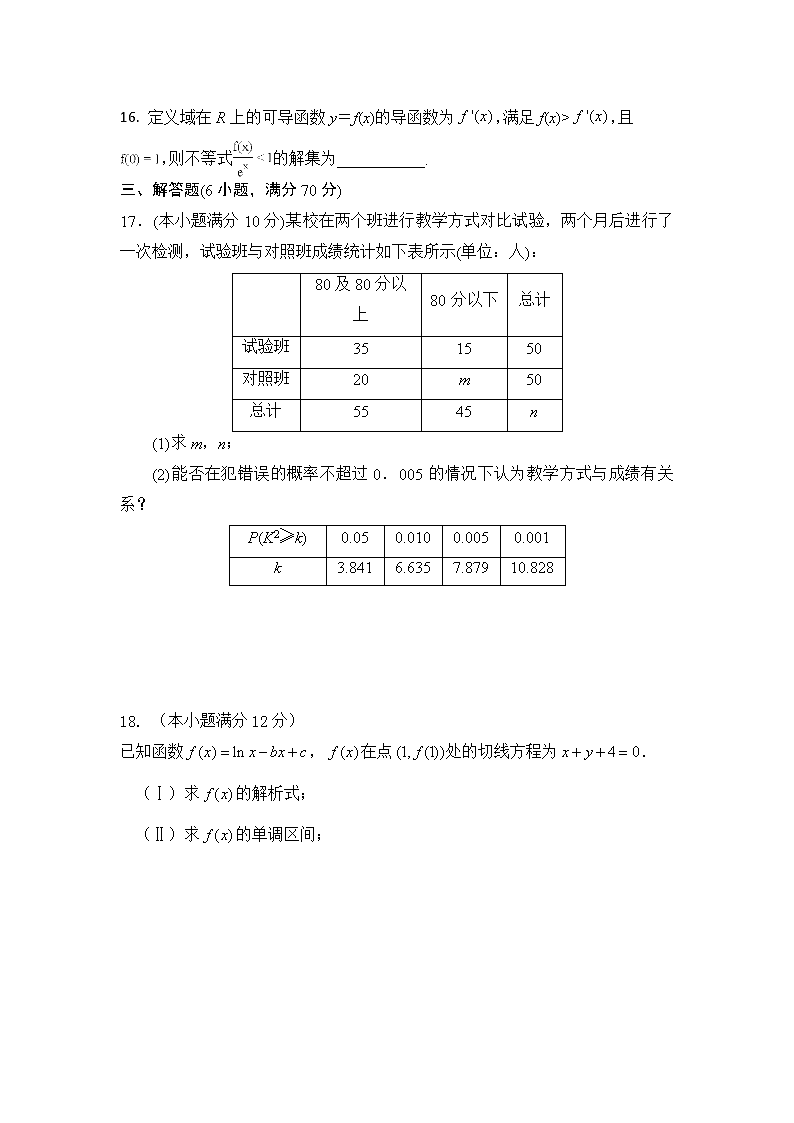定义域在R上的可导函数y＝f(x)的导函数为，满足f(x)>，且 ‎，则不等式的解集为___________.‎ 三、解答题(6小题，满分70分)‎ ‎17．(本小题满分10分)某校在两个班进行教学方式对比试验，两个月后进行了一次检测，试验班与对照班成绩统计如下表所示(单位：人)：‎ ‎80及80分以上 ‎80分以下 总计 试验班 ‎35‎ ‎15‎ ‎50‎ 对照班 ‎20‎ m ‎50‎ 总计 ‎55‎ ‎45‎ n ‎(1)求m，n；‎ ‎(2)能否在犯错误的概率不超过0．005的情况下认为教学方式与成绩有关系？‎ P(K2≥k)‎ ‎0.05‎ ‎0.010‎ ‎0.005‎ ‎0.001‎ k ‎3.841‎ ‎6.635‎ ‎7.879‎ ‎10.828‎ ‎18. （本小题满分12分）‎ 已知函数，在点处的切线方程为．‎ ‎（Ⅰ）求的解析式；‎ ‎（Ⅱ）求的单调区间；‎ ‎19. (本小题满分12分)一盒中装有9张各写有一个数字的卡片，其中4张卡片上的数字是1，3张卡片上的数字是2，2张卡片上的数字是3.从盒中任取3张卡片．‎ ‎(1)求所取3张卡片上的数字完全相同的概率；‎ ‎(2)X表示所取3张卡片上的数字的中位数，求X的分布列与数学期望．‎ ‎(注：若三个数a，b，c满足a≤b≤c，则称b为这三个数的中位数)‎ ‎20．（本小题满分12分）‎ 已知四棱锥的底面为直角梯形，,底面，且是的中点.‎ ‎(1)证明：平面平面 ‎(2)求二面角的余弦值.‎ ‎21.( 本小题满分12分)已知椭圆C的中心在坐标原点,焦点在x轴上,它的一个顶点恰好是抛物线y=x2的焦点,离心率为.‎ ‎(1)求椭圆C的标准方程.‎ ‎(2)过椭圆C的右焦点F作直线l交椭圆C于A,B两点,交y轴于点M,若=m,=n,试判断m+n是否为定值，若是求出m+n的值，若不是请说明理由.‎ ‎22．(本小题满分12分)已知函数f(x)＝ln x－.‎ ‎(1)若f(x)存在最小值且最小值为2，求a的值；‎ ‎(2)设g(x)＝ln x－a，若g(x)＜x2在(0，e]上恒成立，求a的取值范围．‎ ‎2017－2018高二下期中考数学测试卷 班级： 座号： 姓名： 命题人：徐强 审题人：吴元良 一、选择题(12小题，每小题5分,共60分)‎ ‎1．复数的实部是( )‎ A．－2 B．‎2 C．3 D．4‎ 解析：选B　‎ ‎2．张、王两家夫妇各带1个小孩一起到动物园游玩，购票后排队依次入园．为安全起见，首尾一定要排两位爸爸，另外，两个小孩一定要排在一起，则这6人的入园顺序排法种数共有(　　)‎ A．12 B．‎24 C．36 D．48‎ 解析：选B　第一步，将两位爸爸排在两端有2种排法；第二步，将两个小孩视作一人与两位妈妈任意排在中间的三个位置上有‎2A种排法，故总的排法有2×2×A＝24种．‎ ‎3．下列说法正确的是　(　　)‎ A.命题“若x2=1,则x=‎1”‎的否命题为“若x2=1,则x≠‎‎1”‎ B.命题“∀x≥0,x2+x-1<‎0”‎的否定是“∃x0<0,+x0-1<‎‎0”‎ C.命题“若x=y,则sinx=siny”的逆否命题为假命题 D.若“p∨q”为真命题,则p,q中至少有一个为真命题 ‎【解析】选D.‎ ‎4.的展开式中的常数项为　(　　)‎ A.12 B.‎-12 ‎ C.6 D.-6‎ ‎【解析】选A.展开式中的通项公式为Tr+1=·x6-2r·‎ ‎(-2)r·x-r=(-2)r··x6-3r,‎ 令6-3r=0,求得r=2,‎ 故展开式中的常数项为4×3=12.‎ ‎5.使不等式x2-3x<0成立的一个必要不充分条件是　(　　)‎ A.03‎ ‎【解析】选B.‎ ‎6．已知，，是空间的一个基底，设＝＋，＝－，则下列向量中可以与，一起构成空间的另一个基底的是(　　)‎ A． B． C． D．以上都不对 解析　∵a，b，c不共面，‎ ‎∴a＋b，a－b，c不共面，∴p，q，c可构成空间的一个基底．‎ 答案　C ‎7.如图1，已知F是椭圆＋＝1(a>b>0)的左焦点，P是椭圆上的一点，PF⊥x轴，OP∥AB(O为原点)，则该椭圆的离心率是(　　)‎ 图1‎ A. B． C． D． ‎【解析】　因为PF⊥x轴，所以P.‎ 又OP∥AB，所以＝，即b＝c.‎ 于是b2＝c2，‎ 即a2＝‎2c2，所以e＝＝.‎ ‎【答案】　A ‎8. 定积分的值为（ ）‎ A. 0 B. C. 2 D. 4‎ ‎【答案】C ‎9. 若函数的图象上存在两点，使得函数的图象在这两点处的切线互相垂直，则称具有T性质，下列函数中具有T性质的是（ ）‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】根据导数的几何意义，若具有T性质，则存在使或且处切线与x轴垂直.‎ A项，，，有具有T性质，故A项正确；‎ B项，，，切线斜率存在，不满足，不具有T性质，故B项错误；‎ C项，， 不具有T性质，故C项错误；‎ D项，，，不具有T性质，故D项错误.‎ ‎10.若直线y=kx-2与抛物线y2=8x交于A,B两个不同的点,且AB的中点的横坐标为2,则k等于　(　　)‎ A.2或-1 B.‎-1 C.2 D.1± ‎【解析】选C.由消去y得,‎ k2x2-4(k+2)x+4=0,‎ 故Δ=[-4(k+2)]2-4k2×4=64(1+k)>0,‎ 解得k>-1,由x1+x2==4,‎ 解得k=-1或k=2,又因为k>-1,故k=2.‎ ‎【易错警示】本题易忽略Δ>0而错选A.‎ ‎11．设f(x)，g(x)分别是定义在R上的奇函数和偶函数，当x＜0时，f′(x)g(x)－f(x)g′(x)>0，且f(3)＝0，则不等式f(x)g(x)<0的解集是(　　)‎ A．(－3,0)∪(3，＋∞) B．(－3,0)∪(0,3)‎ C．(－∞，－3)∪(3，＋∞) D．(－∞，－3)∪(0,3)‎ 解析：选D　设F(x)＝，‎ 则F′(x)＝，‎ 由题意知：F(x)为奇函数，F(x)在(－∞，0)上递增，F ‎(3)＝0，数形结合易得F(x)<0的解集为(－∞，－3)∪(0,3)，从而f(x)g(x)<0的解集也为(－∞，－3)∪(0,3)．‎ ‎12. 已知是平面的斜线段，为斜足，若与平面成角，过定点的动直线与斜线 成角，且交于点，则动点的轨迹是( )‎ A. 圆 B. 椭圆 C.双曲线 D.抛物线 解析：选D 二、填空题(4小题，每小题5分，共20分)‎ ‎13、双曲线－＝1的渐近线的方程为________．‎ 答案：　y＝±x ‎14.已知随机变量服从正态分布， ，则＝__________‎ 答案：0.34 ‎ ‎15．若三角形内切圆的半径为，三边长为，则三角形的面积等于，根据类比推理的方法，若一个四面体的内切球的半径为，四个面的面积分别是，则四面体的体积　　　　　．‎ 答案： R(S1+S2+S3+S4) ‎ ‎16. 定义域在R上的可导函数y＝f(x)的导函数为，满足，且，则不等式的解集为___________.‎ ‎【答案】‎ ‎【解析】令，，‎ 可得函数在R上为减函数，‎ 又，‎ 故不等式即.‎ 不等式的解集为 .‎ 三、解答题(6小题，满分70分)‎ ‎17．(本小题满分10分)某校在两个班进行教学方式对比试验，两个月后进行了一次检测，试验班与对照班成绩统计如下表所示(单位：人)：‎ ‎80及80分以上 ‎80分以下 总计 试验班 ‎35‎ ‎15‎ ‎50‎ 对照班 ‎20‎ m ‎50‎ 总计 ‎55‎ ‎45‎ n ‎(1)求m，n；‎ ‎(2)能否在犯错误的概率不超过0．005的情况下认为教学方式与成绩有关系？‎ P(K2≥k)‎ ‎0.05‎ ‎0.010‎ ‎0.005‎ ‎0.001‎ k ‎3.841‎ ‎6.635‎ ‎7.879‎ ‎10.828‎ 解：(1)m＝45－15＝30，n＝50＋50＝100．‎ ‎(2)由表中的数据，得K2的观测值为 k＝≈9．091．‎ 因为9．091>7．879，所以能在犯错误的概率不超过0．005的前提下认为教学方式与成绩有关系．‎ ‎18. （本小题满分12分）‎ 已知函数，在点处的切线方程为．‎ ‎（Ⅰ）求的解析式；‎ ‎（Ⅱ）求的单调区间；‎ 解：（Ⅰ）‎ 又切线斜率为－１，故，从而 ‎ 将代入方程得：，从而 ‎，将代入得 故 ‎ ‎（Ⅱ）依题意知，‎ 令，得：，再令，得：‎ 故的单调增区间为，单调减区间为 ‎ ‎19. (本小题满分12分)一盒中装有9张各写有一个数字的卡片，其中4张卡片上的数字是1，3张卡片上的数字是2，2张卡片上的数字是3.从盒中任取3张卡片．‎ ‎(1)求所取3张卡片上的数字完全相同的概率；‎ ‎(2)X表示所取3张卡片上的数字的中位数，求X的分布列与数学期望．‎ ‎(注：若三个数a，b，c满足a≤b≤c，则称b为这三个数的中位数)‎ 解：(1)由古典概型的概率计算公式知所求概率为P＝＝.‎ ‎(2)X的所有可能值为1，2，3，且P(X＝1)＝＝；‎ P(X＝2)＝＝；‎ P(X＝3)＝＝.‎ 故X的分布列为：‎ X ‎1‎ ‎2‎ ‎3‎ P 从而E(X)＝1×＋2×＋3×＝.‎ ‎20．（本小题满分12分）‎ 已知四棱锥的底面为直角梯形，,底面 ‎，且是的中点.‎ ‎(1)证明：平面平面 ‎(2)求二面角的余弦值.‎ ‎【答案】(1)详见解析;(2).‎ ‎ (1)证明：面，，‎ ‎∴由三垂线定理得：.‎ 因而，与面内两条相交直线都垂直，‎ 面，又面，‎ ‎∴面面.‎ ‎(2)作，垂足为，连接.‎ 在中，，又，≌,‎ ‎，故为所求二面角的平面角 ‎，由三垂线定理，得,‎ 在中，，所以.‎ 在等腰三角形中，,‎ ‎,‎ ‎.‎ 故二面角余弦值为.‎ 注：向量法请酌情给分。‎ ‎21.( 本小题满分12分)已知椭圆C的中心在坐标原点,焦点在x轴上,它的一个顶点恰好是抛物线y=x2的焦点,离心率为.‎ ‎(1)求椭圆C的标准方程.‎ ‎(2)过椭圆C的右焦点F作直线l交椭圆C于A,B两点,交y轴于点M,若=m ,=n,试判断m+n是否为定值，若是求出m+n的值，若不是请说明理由.‎ ‎【解析】(1)设椭圆C的标准方程为+=1(a>b>0).‎ 抛物线方程可化为x2=4y,其焦点为(0,1),‎ 则椭圆C的一个顶点为(0,1),即b=1.‎ 由e===.‎ 得a2=5,所以椭圆C的标准方程为+y2=1.‎ ‎(2)m+n 为定值。‎ 易求出椭圆C的右焦点F(2,0),‎ 设A(x1,y1),B(x2,y2),M(0,y0),显然直线l的斜率存在,设直线l的方程为y=k(x-2),‎ 代入方程+y2=1,‎ 得(1+5k2)x2-20k2x+20k2-5=0.‎ 所以x1+x2=,x1x2=.‎ 又=(x1,y1-y0),=(x2,y2-y0),‎ =(x1-2,y1),=(x2-2,y2).‎ 因为=m,=n,‎ 所以m=,n=,‎ 所以m+n=,‎ 又2x1x2-2(x1+x2)= ‎=-,‎ ‎4-2(x1+x2)+x1x2‎ ‎=4-+=,‎ 所以m+n=10.‎ ‎22．(本小题满分12分)已知函数f(x)＝ln x－.‎ ‎(1)若f(x)存在最小值且最小值为2，求a的值；‎ ‎(2)设g(x)＝ln x－a，若g(x)＜x2在(0，e]上恒成立，求a的取值范围．‎ 解：(1)f′(x)＝＋＝(x＞0)，‎ 当a≥0时，f′(x)＞0，f(x)在(0，＋∞)上是增函数，f(x)不存在最小值．‎ 当a＜0时，由f′(x)＝0，得x＝－a，‎ 且0＜x＜－a时f′(x)＜0，‎ x＞－a时f′(x)＞0.‎ ‎∴x＝－a时f(x)取最小值，‎ f(－a)＝ln(－a)＋1＝2，解得a＝－e.‎ ‎(2)g(x)＜x2，即ln x－a＜x2，即a＞ln x－x2，‎ 故g(x)＜x2在(0，e]上恒成立，也就是a＞ln x－x2在(0，e]上恒成立．‎ 设h(x)＝ln x－x2，则h′(x)＝－2x＝，由h′(x)＝0及0＜x≤e，得x＝.‎ 当0＜x＜时h′(x)＞0，当＜x≤e时h′(x)＜0，即h(x)在上为增函数，在上为减函数，所以当x＝时h(x)取得最大值为h＝ln －.‎ 所以g(x)＜x2在(0，e]上恒成立时，‎ a的取值范围为.‎