数学（文）卷·2018届湖北省黄石市三中高二下学期期中考试（2017-04）

数学（文）卷·2018届湖北省黄石市三中高二下学期期中考试（2017-04）

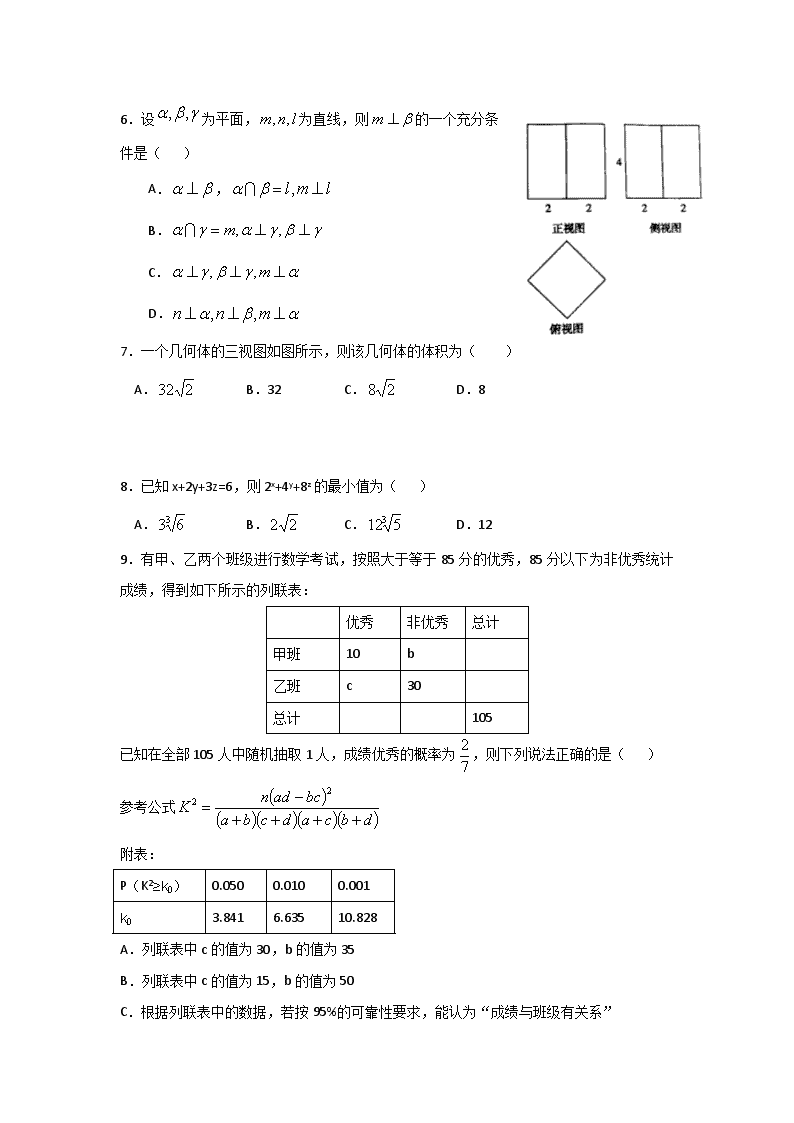
黄石三中2016-2017学年度下学期期中考试 高二年级文科数学试卷 本试卷分第I卷（选择题）和第II卷（非选择题）两部分 第I卷 一、选择题：本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的。‎ ‎1．已知i为虚数单位，在复平面内，复数所对应的点在（ ）‎ A．第一象限 B．第二象银 C．第三象限 D．第四象限 ‎2．某单位有840名职工，现采用系统抽样方法，抽取42人做问卷调查，将840人按1，2，…，840随机编号，则抽取的42人中，编号落入区间[481，720]的人数为（ ）‎ A．11 B．12 C．13 D．14‎ 3． 设函数定义如下表，数列满足，且对任意的自然数均有，则（ ）‎ x ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎4‎ ‎1‎ ‎3‎ ‎5‎ ‎2‎ A．1 B．2 C．4 D．5‎ 4． 已知命题，使；命题，都有。给出下列结论：①命题p是真命题；②命题q是假命题；③命题“”是真命题；④命题“）”是假命题。‎ 其中正确的是（ ）‎ A．②④ B．②③ C． ③④ D．①②③‎ ‎5．从甲乙丙三人中任选两名代表，甲被选中的概率为（ ）‎ A． B． C． D．1‎ ‎6．设为平面，为直线，则的一个充分条件是（ ）‎ A．， B．‎ C． D．‎ ‎7．一个几何体的三视图如图所示，则该几何体的体积为（ ）‎ A． B．32 C． D．8‎ ‎8．已知x+2y+3z=6，则2x+4y+8z的最小值为（ ）‎ A． B． C． D．12‎ 9． 有甲、乙两个班级进行数学考试，按照大于等于85分的优秀，85分以下为非优秀统计成绩，得到如下所示的列联表：‎ 优秀 非优秀 总计 甲班 ‎10[]‎ b 乙班 c[]‎ ‎30‎ 总计 ‎105‎ 已知在全部105人中随机抽取1人，成绩优秀的概率为，则下列说法正确的是（ ）‎ 参考公式 附表：‎ P（K2≥k0）‎ ‎0.050‎ ‎0.010‎ ‎0.001‎ k0‎ ‎3.841‎ ‎6.635‎ ‎10.828‎ A．列联表中c的值为30，b的值为35‎ B．列联表中c的值为15，b的值为50‎ C．根据列联表中的数据，若按95%的可靠性要求，能认为“成绩与班级有关系”‎ D．根据列联表中的数据，若按95%的可靠性要求，不能认为“成绩与班级有关系”‎ ‎10．小王从甲地到乙地往返的时速分别为a和b(a0,b>0)的离心率为2，焦点到渐近线的距离为，则C的焦距等于__________________‎ 15． 如图所示，程序框图（算法流程图）的输出结果是__________ ‎ 16． 若圆上至少有三个不同点到直线的距离为，则直线l的倾斜角的取值范围是________________________‎ 三、 解答题：解答应写出文字说明，证明过程或演算步骤 17． ‎（本小题满分10分）已知的实部为负数，求 13． ‎（本小题满分12分）已知函数 （1） 当m=5时，求的解集；‎ （2） 若关于x的不等式的解集是R，求m的取值范围。‎ 14． ‎（本小题满分12分）为了了解一个小水库中养殖的鱼的有关情况，从这个水库中多个不同位置捕捞出100条鱼，称得每条鱼的质量（单位：千克），并将所得数据分组，画出频率分布直方图（如图所示）。‎ （1） 在表格中填写相应的频率；‎ （2） 估计数据落在[1.15，1.30)中的概率为多少；‎ （3） 将上面捕捞的100条鱼分别作一记号后再放回水库。几天后再从水库的多处不同位置捕捞出120条鱼，其中带有记号的鱼有6条。请根据这一情况来估计该水库中鱼的总条数。‎ 分组 频率 ‎[1.00,1.05)‎ ‎[1.05,1.10)‎ ‎[1.10,1.15)‎ ‎[1.15,1.20)‎ ‎[1.20,1.25)‎ ‎[1.25,1.30]‎ ‎20．（本小题满分12分）如图，四棱锥P-ABCD中，PD平面ABCD，底面ABCD为矩行，PD=DC=4，AD=2，E为PC的中点。‎ （1） 求证：ADPC；‎ （2） 在线段AC上是否存在一点M，使得PA//平面EDM；若存在，求出AM的长；若不存在，请说明理由。[]‎ 13． ‎（本小题满分12分）已知函数 （1） 求的极小值和极大值；‎ （2） 当曲线y=f(x)的切线l的斜率为负数时，求l在x轴上截距的取值范围。‎ ‎22.（本小题满分12分）如图，点P（0，−1）是椭圆 (a>b>0)的一个顶点，C1的长轴是圆C2:x2+y2=4的直径, l1, l2是过点P且互相垂直的两条直线，其中l1交圆C2于A， B两点，l2交椭圆C1于另一点D。‎ ‎(I) 求椭圆C1的方程；‎ ‎(Ⅱ) 求△ABD面积取最大值时直线l1的方程。‎