2017-2018学年江苏省宿迁市高二第二学期期末数学（理）试题（Word版)

2017-2018学年江苏省宿迁市高二第二学期期末数学（理）试题（Word版)

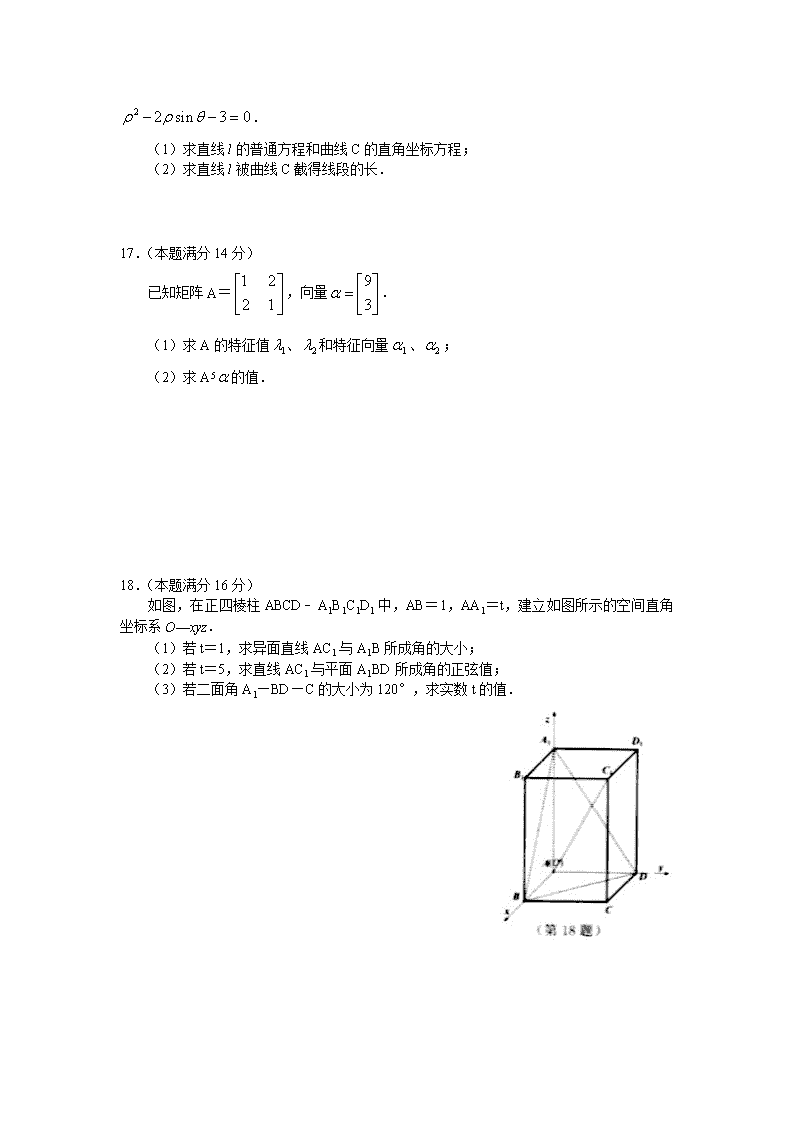
江苏省宿迁市2017~2018学年第二学期期末试卷 高二数学（理）‎ ‎2018．6‎ 注 意 事 项 考生在答题前请认真阅读本注意事项及各题答题要求 ‎1. 本卷共4页，包含填空题（第1题 - 第14题）、解答题（第15题 - 第20题）．本卷满分160分，考试时间为120分钟．考试结束后，请将答题卡交回．‎ ‎2. 答题前，请您务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在答题卡的规定位置．‎ ‎3. 请在答题卡上按照顺序在对应的答题区域内作答，在其他位置作答一律无效．作答必须用0.5毫米黑色墨水的签字笔．请注意字体工整，笔迹清楚．‎ ‎4. 如需作图，须用2B铅笔绘、写清楚，线条、符号等须加黑、加粗．‎ ‎5. 请保持答题卡卡面清洁，不要折叠、破损．一律不准使用胶带纸、修正液、可擦洗的圆珠笔．‎ 一、填空题（本大题共14小题，每小题5分，共计70分．不需要写出解答过程，请将答案填写在答题卡相应的位置上．）‎ ‎1．已知复数z＝(m＋1)＋(m﹣2)i是纯虚数（i为虚数单位），则实数m的值为 ．‎ ‎2．已知点A(1，4，1)，B(﹣2，0，1)，则＝ ．‎ ‎3．若＝，则x的值为 ．‎ ‎4．已知随机变量X服从二项分布X~B(6，)，那么方差V(X)的值为 ．‎ ‎5．三个同学猜同一个谜语，如果每人猜对的概率都是，并且各人猜对与否相互独立，那么他们同时猜对的概率为 ．‎ ‎6．已知矩阵A＝ ，则矩阵A的逆矩阵为 ．‎ ‎7．若从4名男生和3名女生中任选2人参加演讲比赛，则至少选出1名女生的概率为 ‎ ‎ （结果用分数表示）．‎ ‎8．在极坐标系中，已知A(，0)到直线l：，（）的距离为2，则实数m的值为 ．‎ ‎9．设向量＝(2，2m﹣3，n＋2)，＝(4，2m＋1，3n﹣2)，且∥，则·的值为 ．‎ ‎10．圆C1：在矩阵M＝ 对应的变换作用下得到了曲线C2，曲线C2在 矩阵N＝ 对应的变换作用下得到了曲线C3，则曲线C3的方程为 ．‎ ‎11．若的二项展开式中的第3项的二项式系数为15，则的展开式中含项的系数为 ．‎ ‎12．将4个不同的小球放入编号为1，2，3，4的4个盒子中，恰有2个空盒的方法共有 ‎ ‎ 种（用数字作答）．‎ ‎13．对于自然数方幂和（，），，，求和方法如下：‎ ‎ 23﹣13＝3＋3＋1，‎ ‎ 33﹣23＝3×22＋3×2＋1，‎ ‎ ……‎ ‎ (n＋1)3﹣n 3＝3n2＋3n＋1，‎ ‎ 将上面各式左右两边分别，就会有(n＋1)3﹣13＝＋＋n，解得＝n(n＋1)(2n＋1)，类比以上过程可以求得，A，B，C，D，E，FR且与n无关，则A＋F的值为 ．‎ ‎14．化简＝ ．‎ 二、解答题（本大题共6小题，共计90分．请在答题纸指定区域内作答，解答应写出文字说明，证明过程或演算步骤．）‎ ‎15．（本题满分14分）‎ 已知复数，i为虚数单位．‎ ‎（1）求；‎ ‎（2）若复数z满足，求的最大值．‎ ‎16．（本题满分14分）‎ 已知极坐标系的极点与直角坐标系的原点O重合，极轴与x轴的正半轴重合，若直线l的参数方程：（t为参数），曲线C的极坐标方程为：‎ ‎．‎ ‎（1）求直线l的普通方程和曲线C的直角坐标方程；‎ ‎（2）求直线l被曲线C截得线段的长．‎ ‎17．（本题满分14分）‎ 已知矩阵A＝ ，向量．‎ ‎（1）求A的特征值、和特征向量、；‎ ‎（2）求A5的值．‎ ‎18．（本题满分16分）‎ 如图，在正四棱柱ABCD﹣A1B1C1D1中，AB＝1，AA1＝t，建立如图所示的空间直角坐标系O—xyz．‎ ‎（1）若t＝1，求异面直线AC1与A1B所成角的大小；‎ ‎（2）若t＝5，求直线AC1与平面A1BD所成角的正弦值；‎ ‎（3）若二面角A1—BD—C的大小为120°，求实数t的值．‎ ‎19．（本题满分16分）‎ 假设某士兵远程射击一个易爆目标，射击一次击中目标的概率为，三次射中目标或连续两次射中目标，该目标爆炸，停止射击，否则就一直独立地射击至子弹用完．现有5发子弹，设耗用子弹数为随机变量X．‎ ‎（1）若该士兵射击两次，求至少射中一次目标的概率；‎ ‎（2）求随机变量X的概率分布与数学期望E(X)．‎ ‎20．（本题满分16分）‎ 设1，其中pR，n，（r＝0，1，2，…，n）与x无关．‎ ‎（1）若＝10，求p的值；‎ ‎（2）试用关于n的代数式表示：；‎ ‎（3）设，，试比较与的大小．‎ 答案 ‎1．﹣1‎ ‎2．5‎ ‎3．4或9‎ ‎4．‎ ‎5．‎ ‎6．‎ ‎7．‎ ‎8．1‎ ‎9．168‎ ‎10．‎ ‎11．160‎ ‎12．84‎ ‎13．‎ ‎14．‎ ‎15．‎ 解： （1） ……………………6分 ‎（2）设，因为，所以 ……………………8分 在复平面中，复数对应点，‎ 复数对应点的轨迹是以为圆心，2为半径的圆；‎ ‎……………………10分 因为AO=,所以的最大值为． ……………………14分 ‎16．‎ 解：（1）直线的普通方程为， ……………………4分 曲线的普通方程为. ……………………8分 ‎（2）曲线表示以为圆心，2为半径的圆，‎ 圆心到直线的距离， ……………………10分 故直线被曲线截得的线段长为． …………………14分 ‎17．‎ 解： (1)矩阵的特征多项式为，‎ 令，解得，， ………4分 当时，解得； ………6分 当时，解得. ………8分 ‎(2)令，得，求得.　　　…………………10分 所以 ‎ ‎………………14分 ‎ ‎ ‎18．解：（1）当时，，，，，，‎ ‎ 则，‎ ‎， ………………2分 ‎ 故，‎ ‎ 所以异面直线与所成角为．……………………4分 ‎（2）当时，，，，，，‎ ‎ 则，， ‎ ‎ 设平面的法向量，‎ ‎ 则由得，‎ ‎ 不妨取，则， 此时， ……………………7分 设与平面所成角为，因为，‎ 则，‎ ‎ 所以与平面所成角的正弦值为． ……………………10分 ‎ （3）由得，，， ‎ ‎ 设平面的法向量，‎ ‎ 则由得，‎ ‎ 不妨取，则， 此时， ……………13分 ‎ 又平面的法向量，‎ ‎ 故，解得， ‎ ‎ 由图形得二面角大于，所以符合题意．‎ ‎ 所以二面角的大小为，的值为． ……………16分 ‎19． ‎ 解：（1）该士兵射击两次，至少射中一次目标的概率为 ‎ ………4分 ‎（2）耗用子弹数的所有可能取值为2，3，4，5.‎ 当时，表示射击两次，且连续击中目标，； ………6分 当时，表示射击三次，第一次未击中目标，且第二次和第三次连续击中目标，‎ ‎； ………8分 当时，表示射击四次，第二次未击中目标，且第三次和第四次连续击中目标，‎ ‎； ………10分 当时，表示射击五次，均未击中目标，或只击中一次目标，或击中两次目标前四次击中不连续两次或前四次击中一次且第五次击中，或击中三次第五次击中且前四次无连续击中。‎ ‎；‎ ‎………12分 随机变量的数学期望 ‎ ………16分 ‎20． ‎ 解：（1）由题意知，所以. ………2分 ‎（2）当时，，‎ 两边同乘以得：‎ ‎，‎ ‎………………………4分 等式两边对求导，得：‎ ‎………………………6分 令得：‎ ‎，‎ 即 …………………………………………8分 ‎（3），‎ 猜测： ………………………………………………10分 ① 当时，，，，此时不等式成立；‎ ‎………………………………………………11分 ‎②假设时，不等式成立，即：，则时，‎ 所以当时，不等式也成立； ………………………………………………15分 根据①②可知，，均有. …………………………16分 ‎【实际上问题即比较与的大小关系；】‎