人教版高三数学总复习课时作业66
课时作业66 变量间的相关关系、统计案例
一、选择题
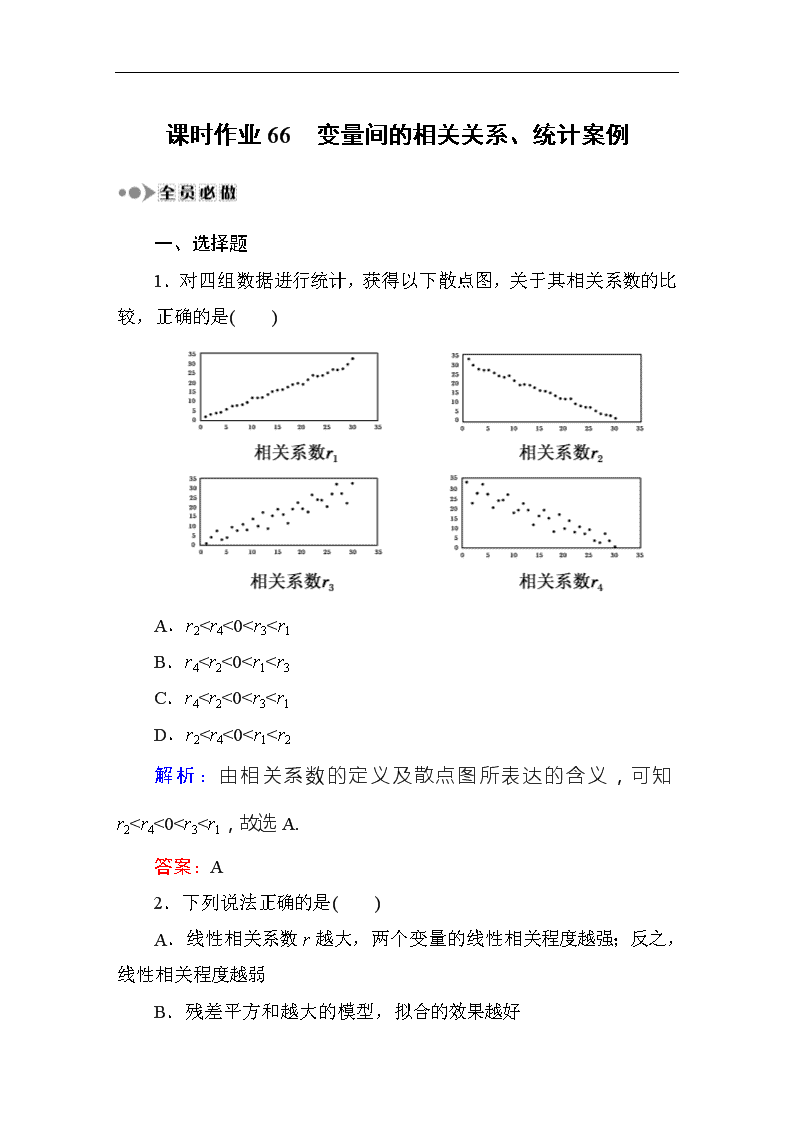
1.对四组数据进行统计,获得以下散点图,关于其相关系数的比较,正确的是( )
A.r2
3.841,因此有95%的把握认为“成绩与班级有关系”.
答案:C
二、填空题
7.考古学家通过始祖鸟化石标本发现:其股骨长度x(cm)与肱骨长度y(cm)的线性回归方程为=1.197x-3.660,由此估计,当股骨长度为50 cm时,肱骨长度的估计值为________cm.
解析:根据回归方程=1.197x-3.660,将x=50代入,得y=56.19,则肱骨长度的估计值为56.19 cm.
答案:56.19
8.在一项打鼾与患心脏病的调查中,共调查了1 671人,经过计算K2的观测值k=27.63,根据这一数据分析,我们有理由认为打鼾与患心脏病是________的.(有关,无关)
解析:由观测值k=27.63与临界值比较,我们有99%的把握说打鼾与患心脏病有关.
答案:有关
9.某数学老师身高176 cm,他爷爷、父亲和儿子的身高分别是173 cm,170 cm和182 cm.因儿子的身高与父亲的身高有关,该老师用线性回归分析的方法预测他孙子的身高为__________cm.
解析:儿子和父亲的身高可列表如下:
父亲身高/x
173
170
176
儿子身高/y
170
176
182
设回归直线方程为 = + x,由表中数据可求得=173,=176,iyi=913 62,=898 05,∴ =1, =- =3,故回归直线方程为 =x+3.当x=182时, =182+3=185.故预测他的孙子的身高为185 cm.
答案:185
三、解答题
10.(2014·辽宁卷)某大学餐饮中心为了解新生的饮食习惯,在全校一年级学生中进行了抽样调查,调查结果如下表所示:
喜欢甜品
不喜欢甜品
合计
南方学生
60
20
80
北方学生
10
10
20
合计
70
30
100
(1)根据表中数据,问是否有95%的把握认为“南方学生和北方学生在选用甜品的饮食习惯方面有差异”;
(2)已知在被调查的北方学生中有5名数学系的学生,其中2名喜欢甜品,现在从这5名学生中随机抽取3人,求至多有1人喜欢甜品的概率.
解:(1)将2×2列联表中的数据代入公式计算,得K2==≈4.762.
由于4.762>3.841,
所以有95%的把握认为南方学生和北方学生在选用甜品的饮食习惯方面有差异.
(2)从5名数学系学生中任取3人的一切可能结果所组成的基本事件空间Ω={(a1,a2,b1),(a1,a2,b2),(a1,a2,b3),(a1,b1,b2),(a1,b2,b3),(a1,b1,b3),(a2,b1,b2),(a2,b2,b3),(a2,b1,b3),(b1,b2,b3)}.
其中ai表示喜欢甜品的学生,i=1,2,bj表示不喜欢甜品的学生,j=1,2,3.Ω由10个基本事件组成,且这些基本事件的出现是等可能的.
用A表示“3人中至多有1人喜欢甜品”这一事件,则A={(a1,b1,b2),(a1,b2,b3),(a1,b1,b3),(a2,b1,b2),(a2,b2,b3),(a2,b1,b3),(b1,b2,b3)}.
事件A是由7个基本事件组成,因而P(A)=.
11.从某居民区随机抽取10个家庭,获得第i个家庭的月收入xi(单位:千元)与月储蓄yi(单位:千元)的数据资料,算得i=80,i=20,iyi=184,=720.
(1)求家庭的月储蓄y对月收入x的线性回归方程=x+;
(2)判断变量x与y之间是正相关还是负相关;
(3)若该居民区某家庭月收入为7千元,预测该家庭的月储蓄.
解:(1)由题意知n=10,=i==8,=i==2,又-n2=720-10×82=80,iyi-n =184-10×8×2=24,由此得b===0.3,a=-b=2-0.3×8=-0.4,故所求回归方程为 =0.3x-0.4.
(2)由于变量y的值随x的值增加而增加(b=0.3>0),故x与y之间是正相关.
(3)将x=7代入回归方程可以预测该家庭的月储蓄为y=0.3×7-0.4=1.7(千元).
1.设某大学的女生体重y(单位:kg)与身高x(单位:cm)具有线性相关关系,根据一组样本数据(xi,yi)(i=1,2,…,n),用最小二乘法建立的回归方程为=0.85x-85.71,则下列结论中不正确的是( )
A.y与x具有正的线性相关关系
B.回归直线过样本点的中心(,)
C.若该大学某女生身高增加1 cm,则其体重约增加0.85 kg
D.若该大学某女生身高为170 cm,则可断定其体重必为58.79 kg
解析:根据线性回归方程中各系数的意义求解.由于线性回归方程中x的系数为0.85,因此y与x具有正的线性相关关系,故A正确.又线性回归方程必过样本中心点(,),因此B正确.由线性回归方程中系数的意义知,x每增加1 cm,其体重约增加0.85 kg,故C正确.当某女生的身高为170 cm时,其体重估计值是58.79 kg,而不是具体值,因此D不正确.
答案:D
2.变量X与Y相对应的一组数据为(10,1),(11.3,2),(11.8,3),(12.5,4),(13,5);变量U与V相对应的一组数据为(10,5),(11.3,4),(11.8,3),(12.5,2),(13,1).r1表示变量Y与X之间的线性相关系数,r2表示变量V与U之间的线性相关系数,则( )
A.r20;对于变量V与U而言,V随U的增大而减小,故V与U负相关,即r2<0,所以选C.
答案:C
3.为了解某班学生喜爱打篮球是否与性别有关,对该班50名学生进行了问卷调查,得到了如下的2×2列联表:
喜爱打篮球
不喜爱打篮球
总计
男生
20
5
25
女生
10
15
25
总计
30
20
50
则在犯错误的概率不超过________的前提下认为喜爱打篮球与性别有关(请用百分数表示).
附:K2=
P(K2≥k0)
0.10
0.05
0.025
0.010
0.005
0.001
k0
2.706
3.841
5.024
6.635
7.879
10.828
解析:K2==
≈8.333>7.879,所以在犯错误的概率不超过0.005的前提下认为喜爱打篮球与性别有关.
答案:0.5%
4.为了解春季昼夜温差大小与某种子发芽多少之间的关系,现在从4月份的30天中随机挑选了5天进行研究,且分别记录了每天昼夜温差与每天100颗种子浸泡后的发芽数,得到如下表格:
日期
4月1日
4月7日
4月15日
4月21日
4月30日
温差x/℃
10
11
13
12
8
发芽数y/颗
23
25
30
26
16
(1)从这5天中任选2天,记发芽的种子数分别为m,n,求事件“m,n均不小于25”的概率;
(2)从这5天中任选2天,若选取的是4月1日与4月30日的两组数据,请根据这5天中的另3天的数据,求出y关于x
的线性回归方程=x+;
(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)中所得的线性回归方程是否可靠?
(参考公式:=,=- )
解:(1)所有的基本事件为(23,25),(23,30),(23,26),(23,16),(25,30),(25,26),(25,16),(30,26),(30,16),(26,16),共10个.
设“m,n均不小于25”为事件A,则事件A包含的基本事件为(25,30),(25,26),(30,26),共3个.
所以P(A)=.
(2)由数据得,另3天的平均数=12,=27,3 =972,32=432,iyi=977,=434,
所以==,=27-×12=-3,
所以y关于x的线性回归方程为=x-3.
(3)依题意得,当x=10时,=22,|22-23|<2;当x=8时,=17,|17-16|<2,
所以(2)中所得到的线性回归方程是可靠的.