数学理卷·2018届吉林省汪清县第六中学高二3月月考（2017-03）

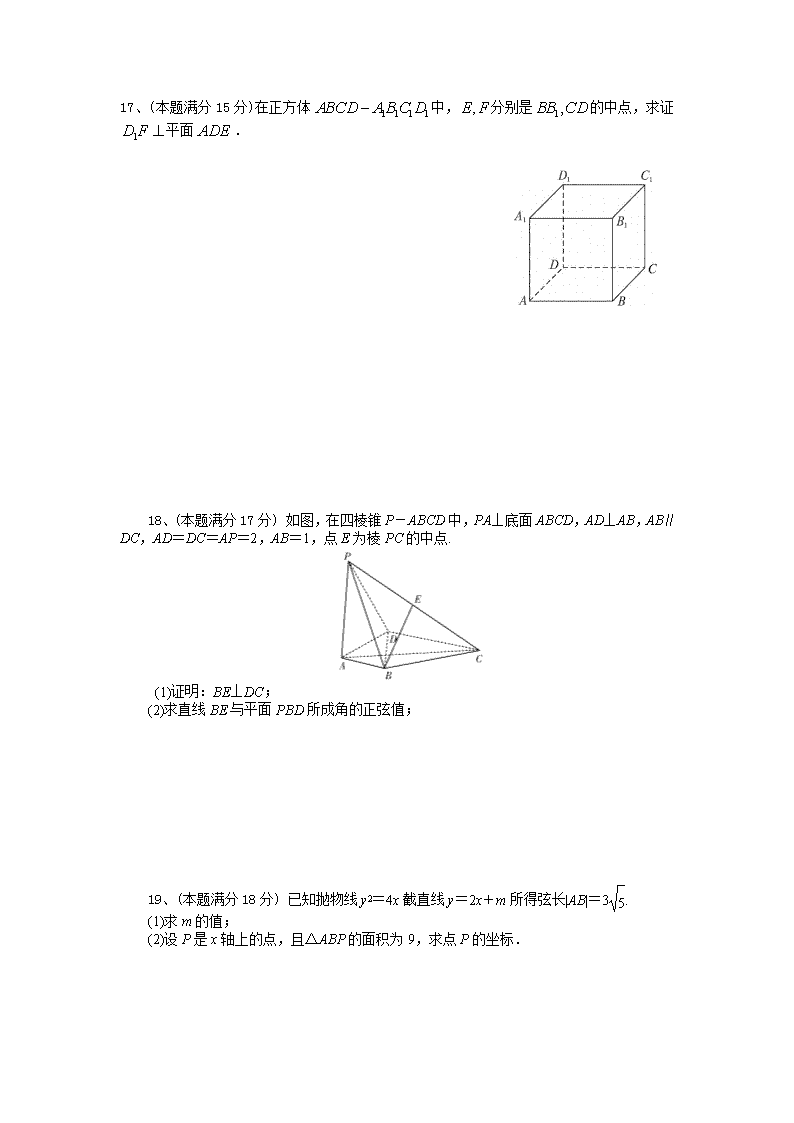
数学理卷·2018届吉林省汪清县第六中学高二3月月考（2017-03）

‎ 2016-2017学年度第二学期 汪清六中三月份月考考试高二理科数学试题 ‎ 总分：150分 时量：90分钟 ‎ ‎　 班级： 姓名： ‎ 一、选择题：（本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合要求的．）‎ ‎1、给出下列命题：①零向量没有方向；②若两个空间向量相等，则它们的起点相同，终点也相同；③若空间向量，满足，则；④若空间向量，，满足，，则；⑤空间中任意两个单位向量必相等．其中正确命题的个数为（ ）‎ ‎ A． 4 B． 3 C． 2 D． 1‎ ‎2、抛物线y2=﹣4x的焦点坐标为（ 　　）‎ ‎ A．（0，﹣2） B．（﹣2，0） C．（0，﹣1） D．（﹣1，0）‎ ‎3、已知平行四边形ABCD的对角线交于点O，且＝，＝，则＝(　 　)‎ A． B． C． D．‎ ‎4、以下四组向量中，互相平行的组数为(　 　)‎ ‎①＝(2,2,1)，＝(3，－2，－2)；②＝(8,4，－6)， ＝(4,2，－3)；‎ ‎③＝(0，－1,1)，＝(0,3，－3)；④＝(－3,2,0)，＝(4，－3,3)‎ A．1组　　　　 B．2组 C．3组 D．4组 ‎5、若椭圆短轴上的两顶点与一焦点的连线互相垂直，则离心率等于（　 　）‎ A． B． C． D．2‎ ‎6、已知A、B、C三点不共线，对于平面ABC外的任一点O，下列条件中能确定点M与点A、B、C一定共面的是 (　 　)‎ A.＝＋＋ B.＝2－－ C.＝＋＋ D.＝＋＋ ‎7、已知F是抛物线x2=8y的焦点，若抛物线上的点A到x轴的距离为5，则|AF|=（　 　）‎ A．4 B．5 C．6 D．7‎ ‎8、已知向量=（1，1，0），=（﹣1，0，2）且k+与2﹣互相垂直，则k的值是（　 　）‎ A．1 B． C． D．‎ ‎9、下列双曲线中，焦点在y轴上且渐近线方程为y=±x的是（　 　）‎ A．x2﹣=1 B． ﹣y2=1 C．﹣x2=1 D．y2﹣=1‎ ‎10、已知F1、F2为双曲线C：x2﹣y2=1的左、右焦点，点P在C上，∠F1PF2=60°，则|PF1|•|PF2|=（　 　）‎ A．2 B．4 C．6 D．8‎ 二、填空题：（本大题共4小题，每小题5分，共20分．把答案填在题中横线上．）‎ ‎11、化简-＋= ‎ ‎12、已知椭圆+=1，F1，F2是椭圆的两个焦点，则|F1F2|=　 ．‎ ‎【来源：全,品…中&高*考+网】13、已知＝(1,2，－2)，则与共线的单位向量坐标为 ‎ ‎【来源：全,品…中&高*考+网】14、若抛物线y2=2px（p＞0）的准线经过双曲线x2﹣y2=1的一个焦点，则p=　 ‎ 三、解答题：(本大题共5小题，共80分． 解答应写出文字说明，证明过程或演算步骤．)‎ ‎15、(本题满分15分)已知，求的值.‎ ‎16、(本题满分15分) 求以直线和两坐标轴的交点为顶点和焦点的椭圆的标准方程。‎ ‎ ‎ ‎17、(本题满分15分)在正方体中，分别是的中点，求证平面．‎ ‎18、(本题满分17分) 如图，在四棱锥P－ABCD中，PA⊥底面ABCD，AD⊥AB，AB∥DC，AD＝DC＝AP＝2，AB＝1，点E为棱PC的中点.‎ ‎ (1)证明：BE⊥DC；‎ ‎(2)求直线BE与平面PBD所成角的正弦值；‎ ‎19、(本题满分18分) 已知抛物线y2＝4x截直线y＝2x＋m所得弦长|AB|＝3.‎ ‎(1)求m的值；‎ ‎(2)设P是x轴上的点，且△ABP的面积为9，求点P的坐标．‎ 汪清六中第一次月考高二理科数学试题答案 ‎ 一、 选择题：‎ DDABB DDDDB 二、填空题：‎ ‎ 11、; 12、　2　; 13、 或； 14、　2　‎ 三、解答题：‎ ‎15、解：由………………………………①‎ 又即 ‎…………………………………②‎ 由①②有：‎ ‎16、解：　 或 ‎17、证明：不妨设已知正方体的棱长为个单位长度，如图所示，建立空间直角坐标系，‎ 则，，‎ ‎ ， ∴，‎ 又，，‎ ‎∴，，所以，平面．‎ ‎18、解:　 依题意，以点A为原点建立空间直角坐标系(如图)，可得B(1,0,0)，C(2,2,0)，D(0,2,0)，P(0,0,2)，由E为棱PC的中点， 得E(1,1,1)．‎ ‎(1)＝(0,1,1)、＝(2,0,0)，故·＝0，所以BE⊥DC.‎ ‎(2)＝(－1,2,0)、＝(1,0，－2)，设n＝(x，y，z)为平面PBD的法向量，则 ，即，‎ 不妨令y＝1，可得n＝(2,1,1)为平面PBD的一个法向量，于是有 cos〈n，〉＝＝＝.‎ 所以，直线BE与平面PBD所成角的正弦值为.‎ ‎19、解：　(1)设A(x1，y1)， B(x2，y2)，‎ 由得4x2＋4(m－1)x＋m2＝0，‎ 由根与系数的关系得x1＋x2＝1－m，x1·x2＝，‎ ‎∴|AB|＝ ‎＝ ‎＝，‎ ‎∵|AB|＝3，∴＝3，解得m＝－4.‎ ‎(2)设P(a,0)，P到直线AB的距离为d，‎ 则d＝＝，‎ 又S△ABP＝|AB|·d，则d＝，‎ ‎∴＝，∴|a－2|＝3，‎ ‎∴a＝5或a＝－1，故点P的坐标为(5,0)或(－1,0)．‎