贵州省遵义市南白中学+2018-2019学年高二上学期第一次月考数学(文)试卷(解析版)x
2018-2019学年贵州省遵义市南白中学
高二上学期第一次月考数学(文)试题此卷只装订不密封
班级 姓名 准考证号 考场号 座位号
数学
注意事项:
1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
2.选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
一、单选题
1.(2018年浙江卷)已知全集U={1,2,3,4,5},A={1,3},则∁UA=
A.∅ B.{1,3} C.{2,4,5} D.{1,2,3,4,5}
2.经过中央电视台《魅力中国城》栏目的三轮角逐,贵州省黔东南州以三轮竞演总分排名第一名问鼎“最具人气魅力城市”.如图统计了黔东南州从2010年到2017年的旅游总人数(万人次)的变化情况,从一个侧面展示了大美黔东南的魅力所在.根据这个图表,在下列给出的黔东南州从2010年到2017年的旅游总人数的四个判断中,错误的是
A.旅游总人数逐年增加
B.2017年旅游总人数超过2015、2016两年的旅游总人数的和
C.年份数与旅游总人数成正相关
D.从2014年起旅游总人数增长加快
3.已知函数f(x)是奇函数,当x>0时,f(x)=log2(x+1),则f(-3)=
A.2 B.-2 C.1 D.-1
4.圆C1:x2+y2+2x=0与圆C2:x2+y2-4x+8y+4=0的位置关系是
A.相交 B.外切 C.内切 D.相离
5.已知向量a=3,1 ,b=0,-1,c=k,3,若a-2b⊥c,则k等于
A.23 B.2 C.-3 D.1
6.执行如图所示的程序框图,输出的k值为
A.2 B.4 C.6 D.8
7.α,β是两个平面,m,n是两条直线,则下列命题中错误的是
A.如果m⊥n,m⊥α,n⊥β,那么α⊥β
B.如果m⊂α,α//β,那么m//β
C.如果α∩β=l,m//α,m⊂β,那么m//l
D.如果m⊥n,m⊥α,n//β,那么α⊥β
8.已知函数fx=x3x2+4,则fx的大致图象为
A. B.
C. D.
9.如图是一个空间几何体的三视图,如果直角三角形的直角边长均为1,那么这个几何体的体积为
A.1 B.12 C.13 D.16
10.若直线2mx-ny-2=0(m>0,n>0)过点(1,﹣2),则1m+2n最小值
A.2 B.6 C.12 D.3+22
11.在锐角ΔABC中,A=2B,则ABAC的取值范围是
A.-1,3 B.1,3 C.(2,3) D.1,2
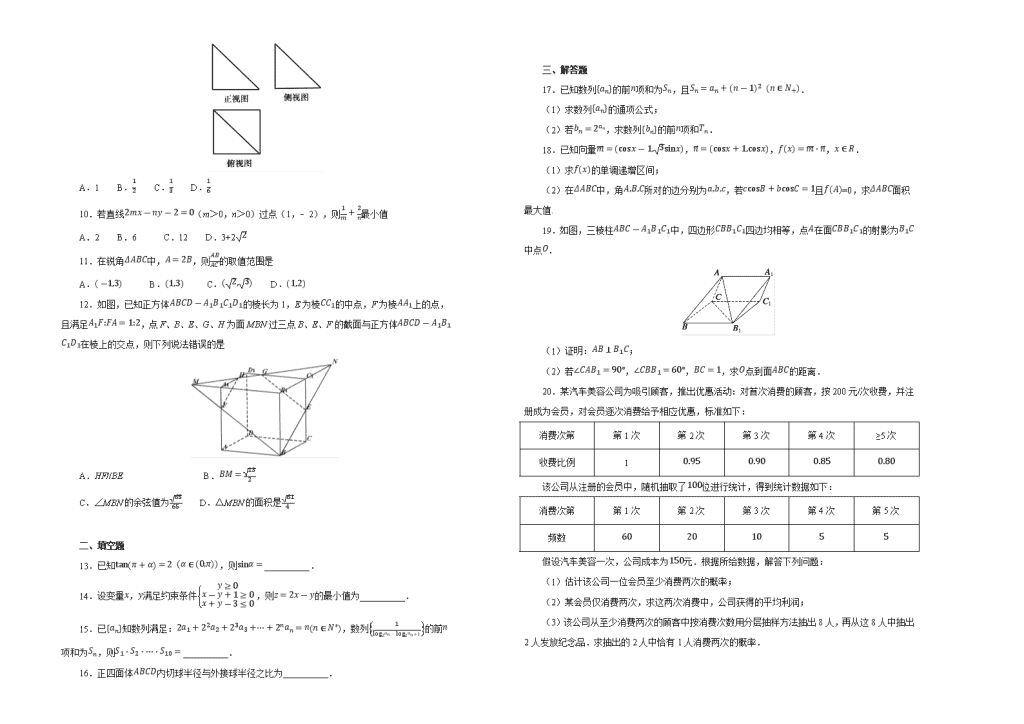
12.如图,已知正方体ABCD-A1B1C1D1的棱长为1,E为棱CC1的中点,F为棱AA1上的点,且满足A1F:FA=1:2,点F、B、E、G、H为面MBN过三点B、E、F的截面与正方体ABCD-A1B1C1D1在棱上的交点,则下列说法错误的是
A.HF//BE B.BM=132
C.∠MBN的余弦值为6565 D.△MBN的面积是614
二、填空题
13.已知tanπ+α=2 (α∈(0,π)),则sinα=__________.
14.设变量x,y满足约束条件y≥0x-y+1≥0x+y-3≤0,则z=2x-y的最小值为__________.
15.已an知数列满足:2a1+22a2+23a3+⋯+2nan=nn∈N*,数列1log2an⋅log2an+1的前n项和为Sn,则S1⋅S2⋅⋯⋅S10=__________.
16.正四面体ABCD内切球半径与外接球半径之比为__________.
三、解答题
17.已知数列an的前n项和为Sn,且Sn=an+(n-1)2 (n∈N+).
(1)求数列{an}的通项公式;
(2)若bn=2an,求数列bn的前n项和Tn.
18.已知向量m=(cosx-1,3sinx),n=(cosx+1,cosx),f(x)=m⋅n,x∈R.
(1)求fx的单调递增区间;
(2)在ΔABC中,角A,B,C所对的边分别为a,b,c,若ccosB+bcosC=1且fA=0,求ΔABC面积最大值.
19.如图,三棱柱ABC-A1B1C1中,四边形CBB1C1四边均相等,点A在面CBB1C1的射影为B1C中点O.
(1)证明:AB⊥B1C;
(2)若∠CAB1=90∘,∠CBB1=60∘,BC=1,求O点到面ABC的距离.
20.某汽车美容公司为吸引顾客,推出优惠活动:对首次消费的顾客,按200元/次收费,并注册成为会员,对会员逐次消费给予相应优惠,标准如下:
消费次第
第1次
第2次
第3次
第4次
≥5次
收费比例
1
0.95
0.90
0.85
0.80
该公司从注册的会员中,随机抽取了100位进行统计,得到统计数据如下:
消费次第
第1次
第2次
第3次
第4次
第5次
频数
60
20
10
5
5
假设汽车美容一次,公司成本为150元.根据所给数据,解答下列问题:
(1)估计该公司一位会员至少消费两次的概率;
(2)某会员仅消费两次,求这两次消费中,公司获得的平均利润;
(3)该公司从至少消费两次的顾客中按消费次数用分层抽样方法抽出8人,再从这8人中抽出2人发放纪念品.求抽出的2人中恰有1人消费两次的概率.
21.如图,四边形ABCD是平行四边形,平面AED⊥平面ABCD,EF//AB,AB=2,BC=EF=1,AE=6,DE=3,∠BAD=π3,CG=12BC.
(Ⅰ)求证:FG//平面BED;
(Ⅱ)求直线EF与平面BED所成角的正弦值.
22.已知过原点的动直线l与圆C1:x2+y2-6x+5=0相交于不同的两点A,B.
(1)求圆C1的圆心坐标和半径r;
(2)求线段AB的中点M的轨迹C的方程;
(3)是否存在实数k,使得直线l1:y=k(x-4)与曲线C只有一个交点?若存在,求出k的取值范围;若不存在,说明理由
2018-2019学年贵州省遵义市南白中学
高二上学期第一次月考数学(文)试题
数学 答 案
参考答案
1.C
【解析】分析:根据补集的定义可得结果.
详解:因为全集U={1,2,3,4,5},A={1,3},所以根据补集的定义得∁UA={2,4,5},
故选C.
点睛:若集合的元素已知,则求集合的交集、并集、补集时,可根据交集、并集、补集的定义求解.
2.B
【解析】
从图表中看出,旅游的总人数逐年增加时正确的;年份数与旅游总人数成正相关,是正确的;从2014年起旅游总人数增长加快是正确的;其中选项B明显错误,故选B.
3.B
【解析】
试题分析:因为函数f(x)是奇函数且x>0时,f(x)=log2(x+1),所以f(-3)=-f(3)=-log2(3+1)=-2,故选B.
考点:1、函数的奇偶性;2、函数的解析式及对数的性质.
4.B
【解析】
试题分析:C1:x2+y2+2x=0的圆心为(-1,0),半径为r1=1,
C2:x2+y2-4x+8y+4=0的圆心为(2,-4),半径r2=4
圆心距离d=5,∴d
4,可排除选项C,D,从而可得结果.
【详解】
因为f-x=-x3-x2+1=-x3x2+1=-fx,
所以函数f(x)是奇函数,其图象关于原点对称,可排除选项B;
又因为f5=12529>4,可排除选项C,D.
故选A.
【点睛】
函数图象的辨识可从以下方面入手:
(1)从函数的定义域,判断图象的左右位置;从函数的值域,判断图象的上下位置.
(2)从函数的单调性,判断图象的变化趋势.
(3)从函数的奇偶性,判断图象的对称性.
(4)从函数的特征点,排除不合要求的图象
9.C
【解析】
【分析】
首先根据三视图,复原的几何体的形状以及特征,结合三视图中的数据,可求出几何体的体积.
【详解】
由三视图可知几何体是底面为正方形,一条侧棱垂直底面的四棱推,
底面正方形的边长为1,棱锥的高为1 ,
所以几何体的体积是13×1×1×1=13,故选C.
【点睛】
本题利用空间几何体的三视图重点考查学生的空间想象能力和抽象思维能力,属于难题.三视图问题是考查学生空间想象能力最常见题型,也是高考热点.观察三视图并将其“翻译”成直观图是解题的关键,不但要注意三视图的三要素“高平齐,长对正,宽相等”,还要特别注意实线与虚线以及相同图形的不同位置对几何体直观图的影响.
10.D
【解析】
【分析】
根据直线2mx﹣ny﹣2=0(m>0,n>0)过点(1,﹣2),建立m,n的关系,利用基本不等式即可求1m+2n的最小值.
【详解】
∵直线2mx﹣ny﹣2=0(m>0,n>0)过点(1,﹣2),
∴2m+2n﹣2=0,即m+n=1,
∵1m+2n=(1m+2n) (m+n)=3+nm+2mn≥3+22,
当且仅当nm=2mn,即n=2m时取等号,
∴1m+2n的最小值为3+22,
故答案为:D
【点睛】
(1)本题主要考查基本不等式,意在考查学生对该知识的掌握水平和分析推理能力.(2)几解题的关键是常量代换1m+2n=1m+2n(m+n),再利用基本不等式求最小值.
11.D
【解析】
【分析】
根据在锐角ΔABC中,每个角都是锐角确定B的范围,利用正弦定理以及三倍角的正弦公式,化简表达式,求出范围即可.
【详解】
在锐角ΔABC中,
0<2∠B<π20<∠B<π20<π-3∠B<π2
可得π6<∠B<π4,
cosB∈22,32,cos2B∈12,34,
所以由正弦定理可知ABAC=cb=sinCsinB=sin3BsinB=3sinB-4sin2BsinB
=3-4sin2B=4cos2B-1∈1,2,故选D.
【点睛】
本题考查正弦定理在解三角形中的应用,三倍角的正弦公式,属于中档题.正弦定理是解三角形的有力工具,其常见用法有以下三种:(1)知道两边和一边的对角,求另一边的对角(一定要注意讨论钝角与锐角);(2)知道两角与一个角的对边,求另一个角的对边;(3)证明化简过程中边角互化;(4)求三角形外接圆半径.
12.C
【解析】
【分析】
利用平面与平面平行性质判断A正误;通过求解三角形判断B,C的正误;通过三角形的面积判断D的正误.
【详解】
因为面AD1//面BC1,且面AD1与面MBN的交线为FH,面BC1与面MBN的交线为BE,所以HF//BE,A正确;
∵A1F//BB1,且A1F:FA=1:2,∴MA1:A1B1=1:2,∴MA1=12,∴B1M=32,在RtΔBB1M中,BM=BB12+B1M2=132,∴B正确;
在RtΔBB1N中,E为棱CC1的中点,∴C1为棱NB1上的中点,∴C1N=1,在RtΔC1EN中,EN=C1E2+C1N2=52,∴BN=5,∵MN=MB12+NB12=52,在ΔBMN中,cos∠MBN=BM2+BN2-MN22BM⋅BN=26565,∴C错误;
∵cos∠MBN=26565,∴sin∠MBN=6165 ∴SΔBMN=12×BM×BN×sin∠MBN=614,,∴D正确,故选C.
【点睛】
本题主要通过对多个命题真假的判断,主要综合考查空间想象能力、面面平行的性质、正方体的截面、余弦定理的应用,属于难题.这种题型综合性较强,也是高考的命题热点,同学们往往因为某一处知识点掌握不好而导致“全盘皆输”,因此做这类题目更要细心、多读题,尽量挖掘出题目中的隐含条件,另外,要注意从简单的自己已经掌握的知识点入手,然后集中精力突破较难的命题.
13.255
【解析】
【分析】
由tanπ+α=2,利用诱导公式可得tanα=2,根据同角三角函数间的关系列方程组,从而可得结果.
【详解】
因为tanπ+α=2,
所以tanα=2,即sinαcosα=2,
结合sin2α+cos2α=1与α∈(0,π)可解得sinα=255,故答案为255.
【点睛】
本题主要考查同角三角函数之间的关系的应用,属于中档题. 同角三角函数之间的关系包含平方关系与商的关系,平方关系是正弦与余弦值之间的转换,商的关系是正余弦与正切之间的转换.
14.-2
【解析】
画出不等式组x-y+1≥0x+y-3≤0y≥0表示的区域如图,结合图形可知 z=2x-y经过点A(-1,0)时,直线y=2x-z在y轴上的截距最大,目标函数z=2x-y取最小值zmin=2×(-1)+0=-2,应填答案-2。
15.111
【解析】
【分析】
由2a1+22a2+23a3+...+2nan=n得2a1+22a2+23a3+...+2n-1an-1=n-1,两式相减化为an=12n,则1log2an⋅log2an+1 =1nn+1=1n-1n+1,由裂项相消法可得Sn= =1-1n+1=nn+1,然后利用累乘法可得结果.
【详解】
∵2a1+22a2+23a3+...+2nan=n,
∴2a1+22a2+23a3+...+2n-1an-1=n-1,
∴2nan=1,
∴an=12n,
∴1log2an⋅log2an+1=1log22-n⋅log22-n+1
=1nn+1=1n-1n+1,
∴Sn=1-12+12-13+...+1n-1n+1
=1-1n+1=nn+1,
∴S1⋅S2⋅S3...S10=12×23×34×...×910×1011=111,
故答案为111.
【点睛】
裂项相消法是最难把握的求和方法之一,其原因是有时很难找到裂项的方向,突破这一难点的方法是根据式子的结构特点,常见的裂项技巧:(1)1nn+k=1k1n-1n+k;(2) 1n+k+n =1kn+k-n; (3)12n-12n+1=1212n-1-12n+1;(4)1nn+1n+2=12 1nn+1-1n+1n+2;此外,需注意裂项之后相消的过程中容易出现丢项或多项的问题,导致计算结果错误.
16.13
【解析】
【分析】
由正四面体的对称性可得正四面体的内切球与外接球球心重合且在正四面体的高上,则R+r=h,将正四面体A-BCD分成以O为顶点,以四面体的四个面为底面的四个正四棱锥,由13sh=4×13sr可得结果.
【详解】
由正四面体的对称性可得正四面体的内切球与外接球球心重合且在正四面体的高上,
设正四面体A-BCD的内切球与外接球球心为O,
正四面体的高为h,
将正四面体A-BCD分成以O为顶点,
以四面体的四个面为底面的四个正四棱锥,
这四个正四棱锥的底面积是正四面体的底面积s,高为内切球的半径r,
设四面体外接球半径为R,则R+r=h,
由四个正四棱锥的体积和等于正四面体的体积可得
13sh=4×13sr⇒r=14h,R=34h⇒rR=13,故答案为13.
【点睛】
本题主要考查多面体内切球与外接球问题,属于中档题. 解答多面体内切球的问题,求出内切球半径是解题的关键,求内切球半径的常见方法有两种:一是对特殊几何体(例如正方体等)往往直接找出球心,求出半径即可;二是对不规则多面体,往往将多面体分成若干个以多面体的面为底面以内切球的球心为高的棱锥,利用棱锥的体积和等于多面体的体积列方程求出内切球半径.
17.(1) an=2n-1;(2) 数列bn的前n项和Tn=23(4n-1).
【解析】
【分析】
(1)Sn=an+(n-1)2,Sn+1=an+1+n2,两式相减化简可得an=2n-1;(2)bn=2an=22n-1,bn+1bn=22n+122n-1=4,数列bn是公比为4的等比数列,利用等比数列的求和公式可得结果.
【详解】
(1)Sn=an+(n-1)2,Sn+1=an+1+n2,
则Sn+1-Sn=an+1-an+n2-(n-1)2=an+1-an+2n-1,
即an+1=an+1-an+2n-1 ,
∴数列an的通项公式为an=2n-1.
(2)bn=2an=22n-1,
∵bn+1bn=22n+122n-1=4, ∴数列bn是公比为4的等比数列,
b1=2,∴数列bn的前n项和Tn=23(4n-1).
【点睛】
本题主要考查数列的通项公式与前n项和公式之间的关系,属于中档题. 已知数列前n项和,求数列通项公式,常用公式an=S1,n=1Sn-Sn-1,n≥2,将所给条件化为关于前n项和的递推关系或是关于第n项的递推关系,若满足等比数列或等差数列定义,用等比数列或等差数列通项公式求出数列的通项公式,否则适当变形构造等比或等数列求通项公式. 在利用Sn与通项an的关系求an的过程中,一定要注意n=1 的情况.
18.(1)fx的单调递增区间kπ-π3,kπ+π6k∈Z;(2)ΔABC为等边三角形时面积最大为34.
【解析】
【分析】
(1)利用平面向量数量积的坐标表示以及二倍角的正弦公式、二倍角的余弦公式以及两角和与差的正弦公式将函数fx化为sin2x+π6-12,利用正弦函数的单调性解不等式,可得到函数fx的递增区间;(2)由fA=0,可得A=π3.由ccosB+bcosC=1利用正弦定理得a=1,由余弦定理结合基本不等式可得得bc≤1,由三角形面积公式可得结果.
【详解】
(1)由题意知fx=cos2x-1+3sinxcosx=sin2x+π6-12.
令2kπ-π2≤2x+π6≤2kπ+π2,得fx的单调递增区间kπ-π3,kπ+π6k∈Z
(2)fA=sin2A+π6-12=0,又0
查看更多