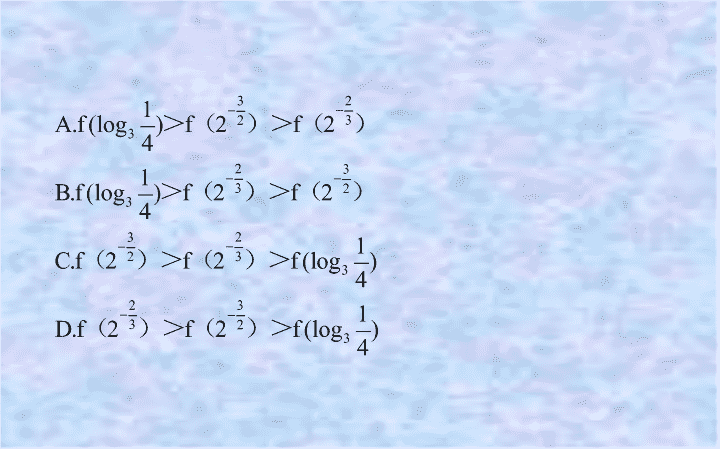2020届高考理科数学二轮专题复习课件:专题1 函数与导数2-1-高考小题 1
第
1
课时 函数的图象与性质
考向一 函数的性质及应用
(
保分题型考点
)
【题组通关】
1.(2019·
全国卷
Ⅲ)
设
f(x)
是定义域为
R
的偶函数
,
且在
(0,+∞)
上单调递减
,
则
(
)
【解析】
选
C.
依据题意
,
函数
f(x)
为偶函数且函数
f(x)
在
(0,+∞)
上单调递减
,
则函数
f(x)
在
(-∞,0)
上单调递
增
;
因为
=f(-log
3
4)=f(log
3
4);
又因为
0< <1
1
或
x≤-1
时与直线
y=x+1
平行
,
此时有一个公共点
,
所以
k∈(0,1)∪(1,4)
时
,
两函数图象恰有两个交点
.
答案
:
(0,1)∪(1,4)
3.
已知函数
y=f(x)
的部分图象如图所示
,
则该函数的解析式可能是
(
)
A.f(x)=x(e
x
-e
-x
)
B.f(x)=ln(e
x
+e
-x
)
C.f(x)=
D.f(x)=ln|x|+1
【解析】
选
B.
函数的图象不经过原点
,
而选项
A
经过原
点
,
排除
A;
选项
C
中当
x=0
时
,f(x)=0,
经过原点排除
C;
f(x)>0,
选项
D
中当
x∈
或
x∈
时
,f(x)<0,
排
除
D.
【拓展提升】
根据函数解析式确定函数图象的技巧
(1)
从定义域判断函数图象的左右位置
,
从值域判断函数图象的上下位置
.
(2)
从单调性判断图象的升降变化趋势
.
(3)
从奇偶性判断图象的对称性
.
(4)
从周期性判断图象的循环往复
.
(5)
结合解析式
,
取特殊值排除不合要求的图象
.
考向三 基本初等函数的图象和性质
(
压轴题型考点
)
【典例】
1.
设 则
a,b,c
的大
小关系是
(
)
A.a b=0.6
1.5
,
函数
y=x
0.6
在
(0,+∞)
上为增函数
;
故
a=0.6
0.6
e
时
,f(x)=x-2ln x,
所以
f′(x)=1- >0,
所以
f(x)=x-2ln x
在
(e,+∞)
上单调递增
,
所以
f(x)>f(e)=e-2,
综上所述
,
函数
f(x)
为
R
上的增函数
,
由
f(6-a
2
)>f(a)
得
6-a
2
>a,
解得
-30.
若在区间
(0,9]
上
,
关于
x
的方程
f(x)=g(x)
有
8
个不同的
实数根
,
则
k
的取值范围是
(
)
【解析】
选
B.
当
x∈(0,2]
时
,f(x)= ,
即
(x-
1)
2
+y
2
=1,y≥0.
又
f(x)
为奇函数
,
其图象关于原点对称
,
其周期为
4,
如
图
,
函数
f(x)
与
g(x)
的图象
(
部分
),
要使
f(x)=g(x)
在
(0,9]
上有
8
个不同的实根
,
只需二者图象有
8
个交点即
可
.
当
g(x)=-
时
,
函数
f(x)
与
g(x)
的图象有
2
个交点
;
当
g(x)=k(x+2)
时
,g(x)
的图象为恒过点
(-2,0)
的直线
,
只需函数
f(x)
与
g(x)
的图象有
6
个交点
.
当
f(x)
与
g(x)
图象相切时
,
圆心
(1,0)
到直线
kx-y+2k=0
的距离为
1,
即
=1,
得
k= ,
函数
f(x)
与
g(x)
的图象有
3
个交点
;
当
g(x)=k(x+2)
过点
(1,1)
时
,
函数
f(x)
与
g(x)
的图象有
6
个交点
,
此时
1=3k,
得
k= .
综上可知
,
满足
f(x)=g(x)
在
(0,9]
上有
8
个实根的
k
的取
值范围为
.
2.(2019·
天津高考
)
已知
a=log
5
2,b=log
0.5
0.2, c=0.5
0.2
,
则
a,b,c
的大小关系为
(
)
A.alog
0.5
0.5=1,
c=0.5
0.2
>0.5
1
= ,
所以
a
查看更多