数学文卷·2017届山东省平阴县第一中学高三下学期开学考试（2017

数学文卷·2017届山东省平阴县第一中学高三下学期开学考试（2017

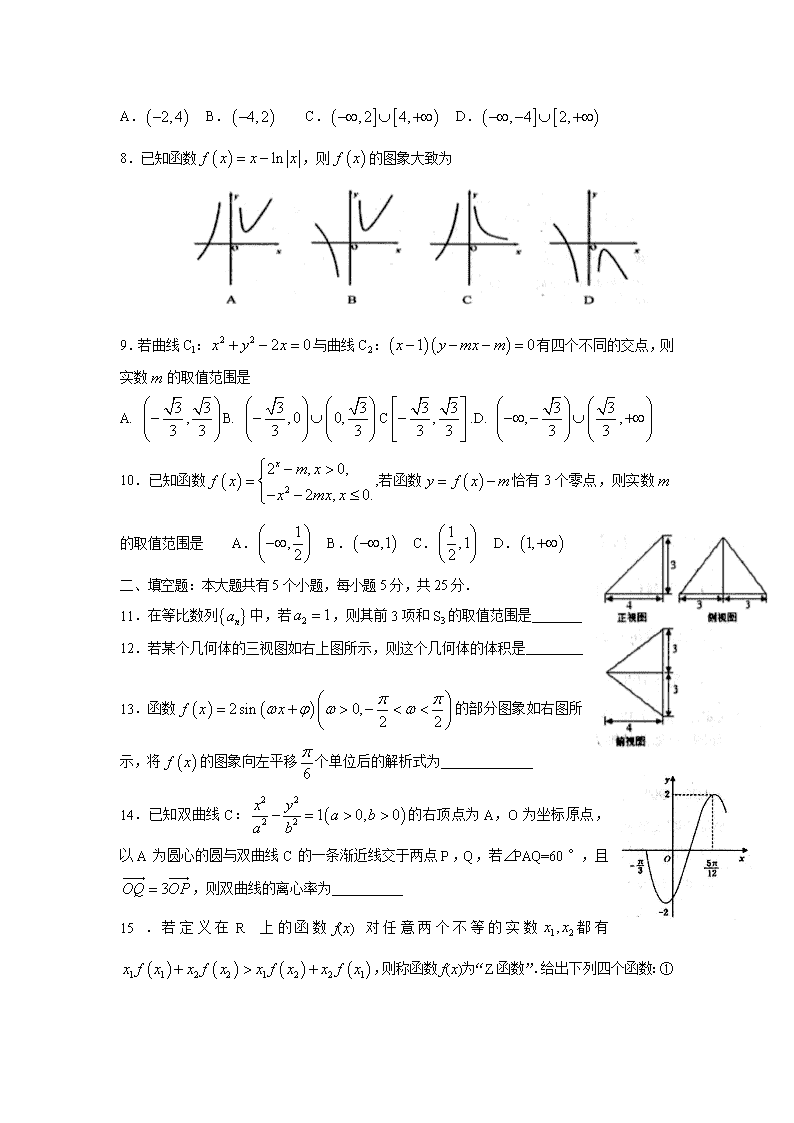
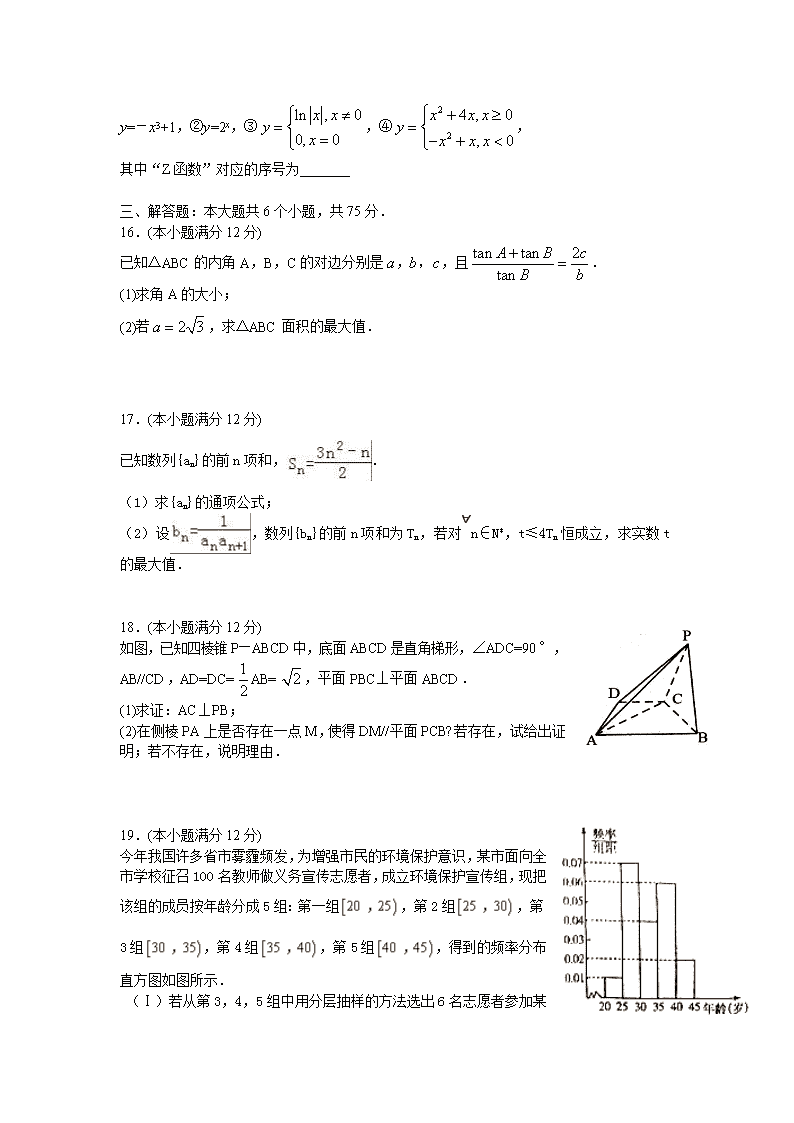
高三下学期检测试题 数学(文科) 2017、2‎ 注意事项：‎ ‎ 1．本试题满分150分，考试时间为120分钟．‎ ‎ 2．使用答题纸时，必须使用0.5毫米的黑色签字笔书写，要字迹工整，笔迹清晰．超出答题区域书写的答案无效；在草稿纸、试题卷上答题无效．‎ 一、选择题：本大题共10小题，每小题5分，共50分．‎ ‎1．已知集合，B=，则= ‎ A． B． C． D．‎ ‎2．设，则关系正确的是 A．b>a>c B． a>b>c C．b>c>a D．c>b>a ‎3．已知是两条不同直线，是三个不同平面，下列命题中正确的是 A．若，则 B．若，则 C．若，则 D．若，则 ‎4．已知函数的最小正周期为，则该函数的图象 ‎ A．关于直线对称 B．关于点对称 C．关于直线对称 D．关于点对称 ‎5．已知x，y满足约束条件，则 z=3x+2y的最大值为 ‎ A．6 B．8 C．10 D．12 ‎ ‎6.已知为平面向量，若与的夹角为，与的夹角为，则=‎ A． B． C． D．‎ ‎7．已知正实数x，y满足，若恒成立，则实数m的取值范围是 A． B． C． D．‎ ‎8．已知函数，则的图象大致为 ‎ ‎9．若曲线Cl：与曲线C2：有四个不同的交点，则实数m的取值范围是 A. B. C.D. ‎ ‎10．已知函数,若函数恰有3个零点，则实数m的取值范围是 A． B． C． D．‎ 二、填空题：本大题共有5个小题，每小题5分，共25分．‎ ‎11．在等比数列中，若，则其前3项和S3的取值范围是 ‎ ‎12．若某个几何体的三视图如右上图所示，则这个几何体的体积是 ‎ ‎13．函数的部分图象如右图所示，将的图象向左平移个单位后的解析式为 ‎ ‎14．已知双曲线C：的右顶点为A，O为坐标原点，以A为圆心的圆与双曲线C的一条渐近线交于两点P，Q，若∠PAQ=60°，且，则双曲线的离心率为 ‎ ‎15．若定义在R上的函数f(x)对任意两个不等的实数都有，则称函数f(x)为“Z函数”．给出下列四个函数：①‎ y=－x3+1，②y=2x，③，④， ‎ 其中“Z函数”对应的序号为 ‎ 三、解答题：本大题共6个小题，共75分．‎ ‎16．(本小题满分12分) ‎ 已知△ABC的内角A，B，C的对边分别是a，b，c，且．‎ ‎(1)求角A的大小；‎ ‎(2)若，求△ABC面积的最大值．‎ ‎17．(本小题满分12分) ‎ 已知数列{an}的前n项和，．‎ ‎（1）求{an}的通项公式；‎ ‎（2）设，数列{bn}的前n项和为Tn，若对∀n∈N*，t≤4Tn恒成立，求实数t的最大值．‎ ‎18．(本小题满分12分)‎ 如图，已知四棱锥P—ABCD中，底面ABCD是直角梯形，∠ADC=90°，AB//CD，AD=DC=AB=，平面PBC⊥平面ABCD．‎ ‎(1)求证：AC⊥PB；‎ ‎(2)在侧棱PA上是否存在一点M，使得DM//平面PCB?若存在，试给出证明；若不存在，说明理由．‎ ‎19．(本小题满分12分)‎ 今年我国许多省市雾霾频发，为增强市民的环境保护意识，某市面向全市学校征召100名教师做义务宣传志愿者，成立环境保护宣传组，现把该组的成员按年龄分成5组：第一组，第2组，第3组，第4组，第5组，得到的频率分布直方图如图所示．‎ ‎ （Ⅰ ‎）若从第3，4，5组中用分层抽样的方法选出6名志愿者参加某社区的宣传活动，应从第3，4，5组各选出多少名志愿者？‎ ‎（Ⅱ）在（Ⅰ）的条件下，该组织决定在这6名志愿者中随机选2名志愿者介绍宣传经验，求第4组至少有1名志愿者被选中的概率． ‎ ‎20．(本小题满分13分)‎ 已知函数在x=1处取得极值2． ‎ ‎(1)求的解析式；‎ ‎(2)设函数，若对任意的，总存在，使得成立，求实数a的取值范围． ‎ ‎21．(本小题满分14分) ‎ 已知点P是椭圆C上任意一点，点P到直线的距离为，到点F(－1，0)的距离为，且，直线l椭圆C交于不同的两点A，B（A，B都在x轴上），∠OFA+∠OFB=180°.‎ ‎(1)求椭圆C的方程；‎ ‎(2)当A为椭圆与y轴正半轴的交点时，求直线l方程；‎ ‎(3)对于动直线l，是否存在一个定点，无论∠OFA如何变化，直线l总经过此定点?若存在，求出该定点的坐标；若不存在，说明理由．‎ 高三数学（文科）参考答案及评分标准 一、选择题 ‎ C B D A D D B A A D 说明：第9题曲线的方程应为：.‎ 二、填空题 ‎ 11. 12. 13. 14. 15. ②④‎ 三、解答题 ‎16.解: （1）因为,由同角三角函数基本关系和正弦定理得，‎ ‎, ……………………………1分 整理得： , ……………………………3分 ‎ 又,所以，‎ 所以. ……………………………5分 又，所以. ……………………………6分 ‎（2）由余弦定理得：，‎ 即：， …………………………………………………8分 所以，当且仅当时取等号，‎ ‎……………………………10分 所以，‎ 即面积的最大值为. ……………………………12分 ‎17.解：∵数列{an}的前n项和，，∴a1=S1=1，………2分 ‎ n≥2时，Sn﹣Sn﹣1=﹣=3n﹣2，………4分 ‎ n=1时，上式成立，∴an=3n﹣2．………5分 （2） 由an=3n﹣2，可得=．………8分 因为，‎ ‎ 所以Tn+1＞Tn，所以数列{Tn}是递增数列．………10分 所以，所以实数t的最大值是1．………12分 ‎18.（1）证明：取的中点，连结，‎ ‎∵，，‎ ‎∴，，‎ ‎∴四边形是平行四边形．‎ 又∵，∴四边形是正方形，‎ ‎∴．‎ ‎∴为等腰三角形，且，‎ ‎∴，∴， ……………………………3分 ‎∵平面平面，平面平面，‎ ‎，平面．‎ ‎∴平面．又∵平面，∴．………………6分 ‎（2）当为侧棱的中点时，平面. ……………………………7分 证明：取的中点，连接 在中， 为中位线，， 由已知，所以.‎ 又， 四边形为平行四边形. . ………10分 又平面，平面，平面. ………12分 ‎19.解：（Ⅰ）由频率分布直方图可得，第3，4，5组的人数分别为：‎ ‎，……1分 ，…2分 ，……3分 故第3，4，5组共有60名志愿者． ‎ 所以，从第3，4，5组中用分层抽样的方法选出6名志愿者参加某社区的宣传活动，各组应选出的人数分别为：， …4分 ， …5分 ， …6分 ‎（Ⅱ）记第3组2名志愿者为；第4组3名志愿者为；第5组1名志愿者为． ‎ 则从这6人中随机选2人，所构成的基本事件有：‎ ‎，，，，，，，，，，，，，，，共15个． ……………………9分 设“从6名志愿者人随机选2名，第4组至少有1名志愿者被选中”为事件． ‎ 则事件包含的基本事件有： ，，，，，，，，，，，，共12个…11分所以…12分 ‎20.解：（1） …………………………1分 因为 在 处取到极值为2，所以,，‎ ‎ 解得 ， ， …4分 经检验，此时 在 处取得极值． 故 ………5分 ‎（2）由（1） 所以 在 上单调递增 ‎ 所以在 上最小值为 所以在 上最小值为 ‎ ‎ …7分依题意有 ‎ 函数的定义域为 ， ……………8分 ‎ ‎ ①当 时， 函数 在 上单调递增，其最小值为 ，符合题意； ‎ ‎ ②当 时，函数在 上有 ，单调递减，在 上 ，单调递增，所以函数最小值为，解不等式，得到 从而知符合题意.‎ ‎ ③当时，显然函数在上单调递减，其最小值为， ‎ 舍去. ……………12分 综上所述，的取值范围为. ……………13分 ‎21.解：（1）设，则， ， ……2分 ‎∴，化简得，∴椭圆的方程为. …4分 ‎（2），∴，……5分 又∵，∴，.‎ 与联立,解得,或者（舍去）.∴, ……7分 于是，∴.直线的方程为. ……8分 ‎（3）联立，得. ……10分 设，∴，，‎ ‎∵，∴.‎ ‎∴， …………13分∴直线方程为，‎ ‎ 故直线总经过定点. …………14分