2017-2018学年辽宁省六校协作体高二上学期期中考试数学（文）试题

2017-2018学年辽宁省六校协作体高二上学期期中考试数学（文）试题

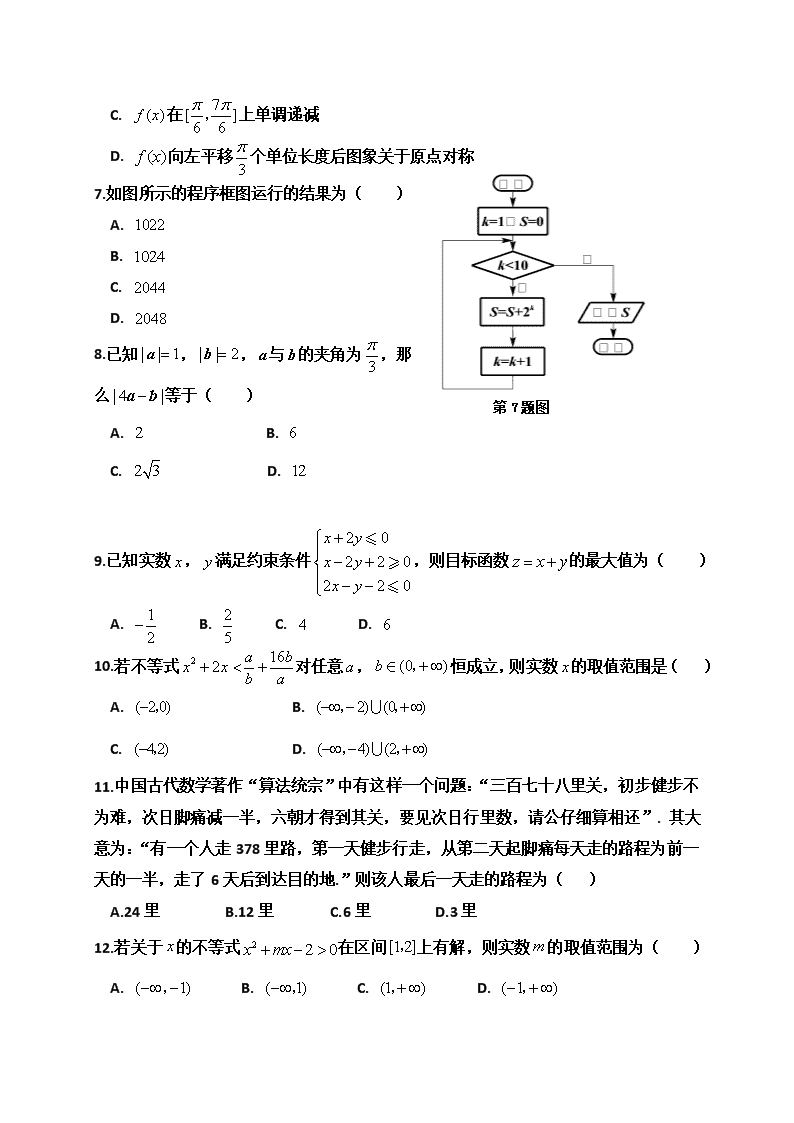
‎2017-2018学年辽宁省六校协作体高二上学期期中考试 数学试题（文科）‎ 命题学校：北镇高中 命题人 ：杨柳 校对人：才忠勇 第Ⅰ卷 一、选择题（本题共12小题，每小题5分.在每小题给出的四个选项中，只有一项是符合题目要求的.）‎ ‎1.已知集合，，则（ ）‎ A. B. C. D.‎ ‎2.函数的定义域为（ ）‎ A. B. C. D.‎ ‎3.如果，那么下列各式一定成立的是（ ）‎ A. B. ‎ C. D. ‎ ‎4.已知等差数列的前项和为，若，，则（ ）‎ A. B. ‎ C. D. ‎ ‎5.某空间几何体的三视图如图所示，则该几何体的体积为(　　)‎ A. B. ‎ C. D. ‎ ‎6.已知函数，则下列说法不正确的是（ ）‎ A. 的一个周期为 B. 的图象关于对称 C. 在上单调递减 D. 向左平移个单位长度后图象关于原点对称 第7题图 ‎7.如图所示的程序框图运行的结果为（ ）‎ A. ‎ B. ‎ C. ‎ D. ‎ ‎8.已知，，与的夹角为，那 么等于（ ）‎ A. B. ‎ C. D. ‎ ‎9.已知实数，满足约束条件，则目标函数的最大值为（ ）‎ A. B. C. D. ‎ ‎10.若不等式对任意，恒成立，则实数的取值范围是（ ）‎ A. B. ‎ C. D. ‎ ‎11.中国古代数学著作“算法统宗”中有这样一个问题：“三百七十八里关，初步健步不为难，次日脚痛减一半，六朝才得到其关，要见次日行里数，请公仔细算相还”. 其大意为：“有一个人走378里路，第一天健步行走，从第二天起脚痛每天走的路程为前一天的一半，走了6天后到达目的地.”则该人最后一天走的路程为（ ）‎ A.24里 B.12里 C.6里 D.3里 ‎12.若关于的不等式在区间上有解，则实数的取值范围为（ ）‎ A. B. C. D. ‎ 第Ⅱ卷 二、填空题（本题共4小题，每小题5分.）‎ ‎13.不等式的解集为 ___________.‎ ‎14.内角的对边分别为.已知，，，则角________.‎ ‎15.若正数，满足，则的最小值为___________.‎ ‎16.设数列是正项数列，若，则______.‎ 三、解答题 （本题共6小题，共70分.）‎ ‎17．（本小题满分10分）‎ 已知集合，.‎ ‎（Ⅰ）若，求;‎ ‎（Ⅱ）若,求实数的取值范围.‎ ‎18．（本小题满分12分）‎ 设数列是公比为正数的等比数列，，.‎ ‎（Ⅰ）求数列的通项公式；‎ ‎（Ⅱ）设是首项为1，公差为2的等差数列，求的前项和.‎ ‎19．（本小题满分12分）‎ 已知锐角，内角，，所对的边分别为，，，且.‎ ‎（Ⅰ）求角；‎ ‎（Ⅱ）若，且的面积为，求的值.‎ ‎20．（本小题满分12分）‎ 已知方程.‎ ‎（Ⅰ）若此方程有两个正实根，求实数的取值范围；‎ ‎（Ⅱ）若此方程有两个实根均在，求实数的取值范围.‎ ‎21．（本小题满分12分）‎ 已知关于的不等式（）.‎ ‎（Ⅰ）若关于的不等式（）的解集为，求,的值；‎ ‎（Ⅱ）解关于的不等式（）.‎ ‎22．（本小题满分12分）‎ 已知数列的前项和为，且满足.‎ ‎（Ⅰ）求数列的通项公式；‎ ‎（Ⅱ）设，，记数列的前项和为，若对任意的，恒成立，求实数的取值范围.‎ ‎2017——2018学年度上学期省六校协作体高二期中考试 数学试题（文科）‎ 参考答案与评分标准 一、选择题 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 B C C D C D A C B C C D 二、填空题 ‎13. 14．‎ ‎15. 16.‎ 三、解答题 ‎17.（本小题满分10分）‎ 解：由题， ,.…………………………………4分 ‎（Ⅰ）当时，，于是………………………6分 ‎（Ⅱ）若,则，即，所以.‎ 故的取值范围为.…………………10分 ‎18. （本小题满分12分）‎ ‎（Ⅰ）设为等比数列的公比，则由，‎ ‎ 得: ，即，……………………2分 ‎ 解得或（舍）‎ ‎ 因此 ………………………………………4分 所以的通项公式为…………………6分 ‎（Ⅱ）因为是首项为1，公差为2的等差数列，‎ 所以；……………………8分 所以…………………10分 所以…………………12分 ‎19.（本小题满分12分）‎ 解：（Ⅰ）由正弦定理，得，………2分 因为，所以，于是，，…………4分[]‎ 又因为锐角，所以，………………………5分 解得.………………………………………6分 ‎（Ⅱ）因为，…………………7分 所以，解得，…………………9分 由余弦定理，得，………………10分 即，……………………………11分 解得.……………………12分 ‎20.（本小题满分12分）[]‎ 解：设.…………………1分 ‎（Ⅰ）由题，，……………………4分 即，解得 ‎ 故的取值范围为.…………………6分 ‎（Ⅱ）由题，，…………10分 即，解得，‎ ‎ 故的取值范围为.………………12分 ‎（注：其他解法请酌情给分.）‎ ‎21.（本小题满分12分）‎ 解：（Ⅰ）由题，方程的两根分别为，，‎ 于是，，………………4分 解得，.…………………5分 ‎（Ⅱ）原不等式等价于，等价于， 6分 ‎（1）当时，原不等式的解集为；…………7分 ‎（2）当时，，，…………………………8分 ‎ ① 当时，原不等式的解集为；……………9分 ‎ ②当时，‎ ‎（ⅰ）若，即时，原不等式解集为……10分 ‎（ⅱ）若，即时，原不等式的解集为；……11分 ‎（ⅲ）当，即时，原不等式的解集为.……………12分 ‎22.（本小题满分12分）‎ ‎ (1)当时，，解得.‎ 当时，，‎ 化简得，……………………………………………..2分 所以是以2为首项，2为公比的等比数列，‎ 所以……………………….………………..4分 ‎(2)因为，……………………….5分 所以…………………..……………6分 所以的前n项和 ‎…………………….8分 因为对任意,恒成立，‎ 所以，整理得：.‎ 因为，…………………………..10分 当且仅当时取等号，所以，…………………………11分 所以要想对任意,恒成立,‎ 则[]‎ 所以实数k的取值范围是…………………12分