2018届二轮复习方法指导-等差数列、等比数列课件（全国通用）

2018届二轮复习方法指导-等差数列、等比数列课件（全国通用）

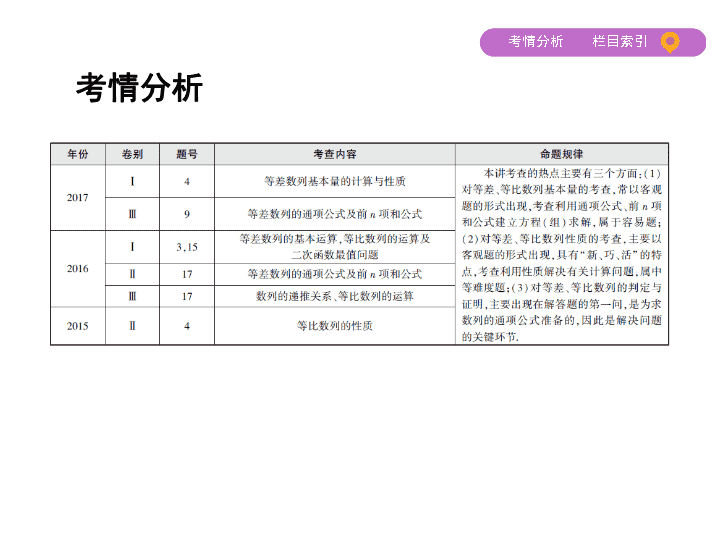
第 1 讲 等差数列、等比数列 考情分析 总纲目录 考点一   等差、等比数列的基本运算 考点二 等差、等比数列的判定与证明 考点三 等差、等比数列的性质 考点一  等差、等比数列的基本运算 (1)通项公式: 等差数列: a n = a 1 +( n -1) d ; 等比数列: a n = a 1 q n -1 ( q ≠ 0). (2)求和公式: 等差数列: S n =   = na 1 +   d ; 等比数列:当 q =1时, S n = na 1 ;当 q ≠ 1时, S n =   =   . 典型例题 　　(1)(2017课标全国Ⅰ,4,5分)记 S n 为等差数列{ a n }的前 n 项和.若 a 4 + a 5 = 24, S 6 =48,则{ a n }的公差为   (　　) A.1　    B.2　    C.4　    D.8 (2)(2017课标全国Ⅱ,17,12分)已知等差数列{ a n }的前 n 项和为 S n ,等比数 列{ b n }的前 n 项和为 T n , a 1 =-1, b 1 =1, a 2 + b 2 =2. (i)若 a 3 + b 3 =5,求{ b n }的通项公式; (ii)若 T 3 =21,求 S 3 . 解析 　(1)设等差数列{ a n }的公差为 d , S 6 =   =48,则 a 1 + a 6 =16= a 2 + a 5 , 又 a 4 + a 5 =24,所以 a 4 - a 2 =2 d =24-16=8,得 d =4,故选C. (2)设{ a n }的公差为 d ,{ b n }的公比为 q , 则 a n =-1+( n -1) d , b n = q n -1 .由 a 2 + b 2 =2得 d + q =3.① (i)由 a 3 + b 3 =5得2 d + q 2 =6.② 联立①和②解得   (舍去)或   因此{ b n }的通项公式为 b n =2 n -1 . (ii)由 b 1 =1, T 3 =21得 q 2 + q -20=0. 解得 q =-5或 q =4. 当 q =-5时,由①得 d =8,则 S 3 =21. 当 q =4时,由①得 d =-1,则 S 3 =-6. 答案 　(1)C 方法归纳 等差(比)数列的运算策略 在进行等差(比)数列项与和的运算时,若条件和结论间的联系不明显,则 均可化成关于 a 1 和 d ( q )的方程组求解,但要注意消元法及整体代入的运 用,以减少计算量. 跟踪集训 1.(2017福州综合质量检测)设等差数列{ a n }的公差 d ≠ 0,且 a 2 =- d ,若 a k 是 a 6 与 a k +6 的等比中项,则 k =   (　　) A.5　    B.6　    C.9　    D.11 答案     C　因为 a k 是 a 6 与 a k +6 的等比中项, 所以   = a 6 a k +6 , 又等差数列{ a n }的公差 d ≠ 0,且 a 2 =- d , 所以[ a 2 +( k -2) d ] 2 =( a 2 +4 d )[ a 2 +( k +4) d ], 所以( k -3) 2 =3( k +3),解得 k =9或 k =0(舍去),故选C. 2.(2017昆明教学质量检测)已知数列{ a n }的前 n 项和为 S n ,且2, S n , a n 成等差 数列,则 S 17 =   (　　) A.0　    B.2　    C.-2　    D.34 答案     B　由2, S n , a n 成等差数列,得2 S n = a n +2,① 2 S n +1 = a n +1 +2,② ②-①,整理得   =-1, 又2 a 1 = a 1 +2,所以 a 1 =2, 所以数列{ a n }是首项为2,公比为-1的等比数列, 所以 S 17 =   =2,故选B. 3.(2017湖北七市(州)联考)已知等比数列{ a n }的前 n 项和 S n =2 n +1 + a ,数列 { b n }满足 b n =2-log 2   . (1)求常数 a 的值; (2)求数列{ b n }的前 n 项和 T n . 解析 　(1)当 n =1时, a 1 = S 1 =2 2 + a =4+ a , 当 n ≥ 2时, a n = S n - S n -1 =2 n +1 + a -(2 n + a )=2 n , ∵{ a n }为等比数列,∴   = a 1 · a 3 ,即(2 2 ) 2 =(4+ a )·2 3 ,解得 a =-2. (2)由(1)知 a n =2 n ,则 b n =2-log 2 2 3 n =2-3 n , ∵ b n +1 - b n =-3对一切 n ∈N * 都成立, ∴{ b n }是以-1为首项,-3为公差的等差数列,即 b 1 =-1, d =-3, ∴ T n = nb 1 +   d =   . 考点二  等差、等比数列的判定与证明 1.证明数列{ a n }是等差数列的两种基本方法 (1)利用定义证明 a n +1 - a n ( n ∈N * )为一常数; (2)利用等差中项,即证明2 a n = a n -1 + a n +1 ( n ≥ 2). 2.证明数列{ a n }是等比数列的两种基本方法 (1)利用定义证明   ( n ∈N * )为一常数; (2)利用等比中项,即证明   = a n -1 a n +1 ( n ≥ 2). 典型例题 (2017贵州适应性考试)已知数列{ a n }满足 a 1 =1,且 na n +1 -( n +1) a n =2 n 2 +2 n . (1)求 a 2 , a 3 ; (2)证明数列   是等差数列,并求{ a n }的通项公式. 解析 　(1)由已知得 a 2 -2 a 1 =4, 则 a 2 =2 a 1 +4,又 a 1 =1,所以 a 2 =6. 由2 a 3 -3 a 2 =12得2 a 3 =12+3 a 2 ,所以 a 3 =15. (2)由已知 na n +1 -( n +1) a n =2 n ( n +1),得   =2,即   -   =2, 所以数列   是首项为1,公差为2的等差数列. 则   =1+2( n -1)=2 n -1,所以 a n =2 n 2 - n . 方法归纳 (1)判定一个数列是等差(比)数列,可以利用通项公式或前 n 项和公式,但 不能将其作为证明方法; (2)   = q 和   = a n -1 a n +1 ( n ≥ 2)都是数列{ a n }为等比数列的必要不充分条 件,判定时还要看各项是否为零. 跟踪集训 1.已知 S n 是等比数列{ a n }的前 n 项和,且 S 3 , S 9 , S 6 成等差数列,下列结论正确 的是   (　　) A. a 1 , a 7 , a 4 成等差数列　    B. a 1 , a 7 , a 4 成等比数列 C. a 1 ,2 a 7 , a 4 成等差数列　    D. a 1 ,2 a 7 , a 4 成等比数列 答案     A　显然 q =1时不合题意,依题意得 S 3 + S 6 =2 S 9 , 即   (1- q 3 )+   (1- q 6 )=   (1- q 9 ) ⇒ 1+ q 3 =2 q 6 ⇒ a 1 + a 1 q 3 =2 a 1 q 6 ⇒ a 1 + a 4 =2 a 7 , ∴ a 1 , a 7 , a 4 成等差数列. 2.(2017课标全国Ⅰ,17,12分)记 S n 为等比数列{ a n }的前 n 项和.已知 S 2 =2, S 3 =-6. (1)求{ a n }的通项公式; (2)求 S n ,并判断 S n +1 , S n , S n +2 是否成等差数列. 解析 　(1)设{ a n }的公比为 q ,由题设可得   解得 q =-2, a 1 =-2.故{ a n }的通项公式为 a n =(-2) n . (2)由(1)可得 S n =   =-   +(-1) n ·   . 由于 S n +2 + S n +1 =-   +(-1) n ·   =2   =2 S n ,故 S n +1 , S n , S n +2 成等差数列. 考点三  等差、等比数列的性质 等差数列 等比数列 性 质 (1)若 m , n , p , q ∈N * ,且 m + n = p + q ,则 a m + a n = a p + a q ; (2) a n = a m +( n - m ) d ; (3) S m , S 2 m - S m , S 3 m - S 2 m , … 仍成等差数列 (1)若 m , n , p , q ∈N * ,且 m + n = p + q ,则 a m a n = a p a q ; (2) a n = a m q n - m ; (3) S m , S 2 m - S m , S 3 m - S 2 m , … 仍成等比数列( q ≠ -1) 典型例题 (1)(2017云南11校跨区调研)已知数列{ a n }是等比数列, S n 为其前 n 项 和,若 a 1 + a 2 + a 3 =4, a 4 + a 5 + a 6 =8,则 S 12 =   (　　) A.40　    B.60　    C.32　    D.50 (2)设 S n 为等差数列{ a n }的前 n 项和,( n +1) S n < nS n +1 ( n ∈N * ).若   <-1,则 (    　) A. S n 的最大值是 S 8 　    B. S n 的最小值是 S 8 C. S n 的最大值是 S 7 　    D. S n 的最小值是 S 7 解析 　(1)由等比数列的性质可知,数列 S 3 , S 6 - S 3 , S 9 - S 6 , S 12 - S 9 是等比数列,即 数列4,8, S 9 - S 6 , S 12 - S 9 是等比数列,则 S 9 - S 6 =16, S 12 - S 9 =32,因此 S 12 =4+8+16+32 =60,故选B. (2)由( n +1) S n < nS n +1 得 ( n +1)   < n   , 整理得 a n < a n +1 , 所以等差数列{ a n }是递增数列, 又   <-1,所以 a 8 >0, a 7 <0, 所以数列{ a n }的前7项为负值,即 S n 的最小值是 S 7 ,故选D. 答案 　(1)B　(2)D 方法归纳 应用数列性质解题的方法 (1)解决此类问题的关键是抓住项与项之间的关系及项的序号之间的关 系,从这些特点入手选择恰当的性质进行求解. (2)应牢固掌握等差、等比数列的性质,特别是等差数列中,“若 m + n = p + q ,则 a m + a n = a p + a q ( m , n , p , q ∈N * )”这一性质与求和公式 S n =   的综合 应用. 跟踪集训 1.(2017太原模拟试题)已知 S n 是等差数列{ a n }的前 n 项和,2( a 1 + a 3 + a 5 )+3( a 8 + a 10 )=36,则 S 11 =   (　　) A.66　    B.55　    C.44　    D.33 答案     D　因为 a 1 + a 5 =2 a 3 , a 8 + a 10 =2 a 9 , 所以2( a 1 + a 3 + a 5 )+3( a 8 + a 10 )=6 a 3 +6 a 9 =36, 所以 a 3 + a 9 =6, 所以 S 11 =   =   =33,故选D. 2.一个项数为偶数的等比数列{ a n },全部各项之和为偶数项之和的4倍, 前3项之积为64,则 a 1 =   (　　) A.11　    B.12　    C.13　    D.14 答案     B　设数列{ a n }的公比为 q ,全部奇数项、偶数项之和分别记为 S 奇 、 S 偶 ,由题意知, S 奇 + S 偶 =4 S 偶 ,即 S 奇 =3 S 偶 .因为数列{ a n }的项数为偶数,所以 q =   =   . 又 a 1 ( a 1 q )( a 1 q 2 )=64,所以   q 3 =64,故 a 1 =12. 3.在数列{ a n }中, a 1 =5,( a n +1 -2)( a n -2)=3( n ∈N * ),则该数列的前2 016项的和 是 　　　     . 答案 　8 064 解析 　因为( a n +1 -2)( a n -2)=3,所以( a n +2 -2)( a n +1 -2)=3,因此 a n +2 -2= a n -2,即 a n +2 = a n ,所以数列{ a n }是以2为周期的数列.又 a 1 =5,因此( a 2 -2)( a 1 -2)=3,故 a 2 =3, a 1 + a 2 =8.注意到2 016=2 × 1 008,因此该数列的前2 016项的和等于1 008( a 1 + a 2 )=8 064. 1.(2017贵州适应性考试)已知数列{ a n }满足 a n =   a n +1 ,若 a 3 + a 4 =2,则 a 4 + a 5 =   (　　) A.   　    B.1　    C.4　    D.8 随堂检测 答案     C　解法一:因为 a n =   a n +1 , a 3 + a 4 =2,所以 a n ≠ 0,可得   =2,所以{ a n } 为等比数列,由 a n = a m q n - m ,得 a 3 + a 3 × 2 4-3 =2,解得 a 3 =   ,所以 a n = a 3 q n -3 =   × 2 n -3 ,由 此可得 a 4 = a 3 × 2=   , a 5 = a 3 × 2 2 =   ,所以 a 4 + a 5 =   +   =   =4. 解法二:已知 a n =   a n +1 ,可得 a n +1 =2 a n , 所以 a 4 + a 5 =2 a 3 +2 a 4 =2( a 3 + a 4 )=2 × 2=4. 2.已知等比数列{ a n }的公比为 q ,前 n 项和为 S n ,若点( n , S n )在函数 y =2 x +1 + m 的图象上,则 m =   (　　) A.-2　    B.2　    C.-3　    D.3 答案     A　易知 q ≠ 1, S n =   =   -   q n =   -   q n +1 ,又点( n , S n )在函数 y =2 x +1 + m 的图象上, 所以 S n =2 n +1 + m ,所以 q =2,   解得 m =-2. 3.(2017北京,10,5分)若等差数列{ a n }和等比数列{ b n }满足 a 1 = b 1 =-1, a 4 = b 4 = 8,则   = 　　　     . 答案 　1 解析 　设等差数列{ a n }的公差为 d ,等比数列{ b n }的公比为 q . ∵ a 1 = b 1 =-1, a 4 = b 4 =8, ∴   ∴   ∴ a 2 =2, b 2 =2.∴   =   =1. 4.(2017广西三市第一次联考)已知数列{ a n }的前 n 项和为 S n ,且 S n =2 n -1( n ∈N * ). (1)求数列{ a n }的通项公式; (2)设 b n =log 4 a n +1,求{ b n }的前 n 项和 T n . 解析 　(1)当 n ≥ 2时, a n = S n - S n -1 =2 n -1 . 当 n =1时, a 1 =2-1=1,满足 a n =2 n -1 , ∴数列{ a n }的通项公式为 a n =2 n -1 ( n ∈N * ). (2)由(1)得, b n =log 4 a n +1=   , 则 b n +1 - b n =   -   =   , ∴数列{ b n }是首项为1,公差 d =   的等差数列, ∴ T n = nb 1 +   d =   .