2019学年高二数学下学期期末考试试题 文新版目标版

2019学年高二数学下学期期末考试试题 文新版目标版

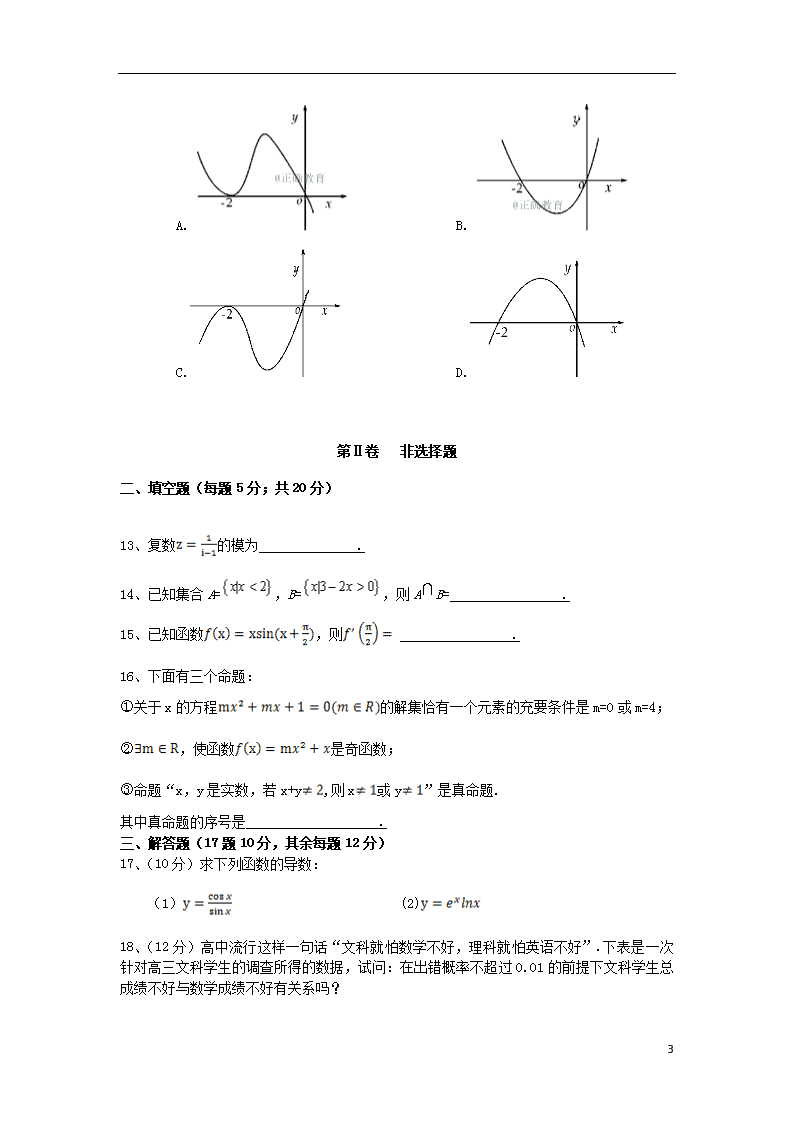
‎2016~2017学年2019高二期末文科数学试卷 考试时间：120分 满分：150分 注意事项： 1.答题前填好自己的姓名、班级、考号等信息. 2.请将答案正确填写在答题卡上.‎ 第Ⅰ卷 选择题 一、单选题（每题5分；共60分）‎ ‎1、已知全集U={1，2，3，4}，集合A={1，2}，B={2，3}，则（A∪B）=（   ）‎ A、{1，3，4} B、{3，4} C、{3} D、{4}‎ ‎2、复数z＝i·(1＋i)(i为虚数单位)在复平面上对应的点位于(　　)．‎ A、第一象限 B、第二象限 C、第三象限 D、第四象限 ‎3、设a∈R，则“a＞1”是“a2＞1”的（    ）‎ A、充分不必要条件 B、必要不充分条件 C、充要条件 D、既不充分也不必要条件 ‎4、设命题：，＞，则为(     ) ‎ A、， B、， C、， D、，‎ ‎5、函数的极大值是(     )‎ A、1 B、0 C、2 D、不存在 ‎6、四名同学根据各自的样本数据研究变量x，y之间的相关关系，并求得回归直线方程，分别得到以下四个结论：‎ ‎①y与x负相关且＝2.347x－6.423；‎ ‎②y与x负相关且＝－3.476x＋5.648；‎ ‎③y与x正相关且＝5.437x＋8.493；‎ ‎④y与x正相关且＝－4.326x－4.578.‎ 其中一定不正确的结论的序号是(　　)‎ A、①② B、②③ C、③④ D、①④‎ ‎7、用反证法证明命题：“已知为实数，则方程少有一个实根”时，要做的假设是(　　)‎ 6‎ A、方程没有实根 B、方程至多有一个实根 C、方程至多有两个实根 D、方程恰好有两个实根 ‎8、若曲线y=在点（0.b）处的切线方程是，则(　　)‎ A、， B、， ‎ C、， D、， 9、如图所示，程序框图(算法流程图)的输出结果是(　　)．‎ A、 B、 C、 D、‎ ‎10、甲、乙、丙、丁四位歌手参加比赛，只有其中一位获奖．有人走访了四位歌手，甲说：“是乙或丙获奖．”乙说：“甲、丙都未获奖．”丙说：“我获奖了．”丁说：“是乙获奖．”四位歌手的话只有两句是对的，则获奖的歌手是(   ) ‎ A、甲 B、乙 C、丙 D、丁 ‎11、设函数f(x)=ln(1+x)-ln(1-x)，则f(x)是(     ) ‎ A、奇函数，且在（0,1）上是增函数   B、奇函数，且在（0,1）上是减函数 C、偶函数，且在（0,1）上是增函数  D、偶函数，且在（0,1）上是减函数 ‎12、设函数f(x) 在R上可导，其导函数为(x),且函数f(x)在x=-2处取得极小值，则函数的图像可能是（ ）‎ 6‎ A. B. ‎ C. D.‎ 第Ⅱ卷 非选择题 二、填空题（每题5分；共20分）‎ ‎13、复数的模为 .‎ ‎14、已知集合A=，B=，则AB= .‎ ‎15、已知函数，则 .‎ ‎16、下面有三个命题：‎ 关于x的方程的解集恰有一个元素的充要条件是m=0或m=4；‎ ，使函数是奇函数；‎ 命题“x，y是实数，若x+y,则x或y”是真命题.‎ 其中真命题的序号是 .‎ 三、解答题（17题10分，其余每题12分）‎ ‎17、（10分）求下列函数的导数：‎ ‎（1） (2) ‎18、（12分）高中流行这样一句话“文科就怕数学不好，理科就怕英语不好”.下表是一次针对高三文科学生的调查所得的数据，试问：在出错概率不超过0.01的前提下文科学生总成绩不好与数学成绩不好有关系吗？ ‎ 6‎ 总成绩好 总成绩不好 总计 数学成绩好 ‎20‎ ‎10‎ ‎30‎ 数学成绩不好 ‎5‎ ‎15‎ ‎20‎ 总计 ‎25‎ ‎25‎ ‎50‎ ‎ ‎ P(K2≥k)‎ ‎0.100‎ ‎0.050‎ ‎0.010‎ ‎0.001‎ k ‎2.706‎ ‎3.841‎ ‎6.635‎ ‎10.828‎ ‎19、（12分）随着我国经济的发展，居民的储蓄存款逐年增长．设某地区城乡居民人民币储蓄存款（年底余额）如下表：‎ 年份 ‎2010‎ ‎2011‎ ‎2012‎ ‎2013‎ ‎2014‎ 时间代号t ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ 储蓄存款y（千亿元）‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎10‎ ‎（1）求y关于t的回归方程=t+．（7分）‎ ‎（2）用所求回归方程预测该地区2015年（t=6）的人民币储蓄存款．（5分）‎ 附：回归方程=t+中 ‎20、（12分）已知p：，q：，若p是q的充分条件，求正实数m的取值范围.‎ ‎21、（12分）已知函数 ‎（1）求f(x)的单调递减区间.（5分）‎ ‎（2）若f(x)在区间[-2，2]上的最大值为20，求它在该区间上的最小值.（7分）‎ ‎22、（12分）设函数f(x)= ‎（1）若,求f(x)的单调区间.（5分）‎ ‎（2）若当时，,求的取值范围.（7分）‎ 6‎ 高二文科数学答案解析 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ D B A C D D A A D C A B ‎13、 14、（-，）或15、16、 ‎17、 ‎18、解：依题意，计算K2的观测值：k＝≈8.333＞6.635. ∵P(K2≥6.635)＝0.01，∴犯错误的概率不超过0.01.所以在犯错误的概率不超过0.01的前提下，认为“文科学生总成绩不好与数学成绩不好有关系”. ‎ ‎19、由题意，=3，=7.2，‎ ‎=55﹣5×32=10，=120﹣5×3×7.2=12，‎ ‎∴=1.2，=7.2﹣1.2×3=3.6，‎ ‎∴y关于t的回归方程=1.2t+3.6．‎ ‎（Ⅱ）t=6时，=1.2×6+3.6=10.8（千亿元）．‎ ‎20、:解不等式x2-8x-20＞0得p:A={x|x＞10或x＜-2}.‎ 解不等式x2-2x+1-m2＞0得q:B={x|x＞1+m,或x＜1-m,m＞0}.‎ 依题意,pq,说明AB.‎ 于是，有解得0＜m≤3.‎ ‎∴正实数m的取值范围是0＜m≤3. ‎ 6‎ ‎21、解：（Ⅰ）， 令，解得x＜-1或x＞3， 所以函数f（x）的单调递减区间为； （Ⅱ）因为，，所以f（2）＞f（-2），于是有22+a=20，解得a=-2，故， 因为（-1，3）上，所以f（x）在[-1，2]上单调递增， 又由于f（x）在 [-2，-1]上单调递减，因此f（2）和f（-1）分别是f（x）在区间[-2，2]上的最大值和最小值， 因此f（-1）=1+3-9-2=-7， 即函数f（x）在区间[-2，2]上最小值为-7。‎ ‎22、解（Ⅰ）时，，。当时;当时，;当时，。故在，单调递增，在（-1，0）单调递减。‎ ‎（Ⅱ）。令，则。‎ 若，则当时，，为增函数，而，从而当x≥0时≥0，即≥0.‎ 若，则当时，，为减函数，而，从而当时＜0，即＜0.综合得的取值范围为 6‎