数学文（实验部）卷·2019届河北省安平中学高二上学期期末考试（2018-01）

数学文（实验部）卷·2019届河北省安平中学高二上学期期末考试（2018-01）

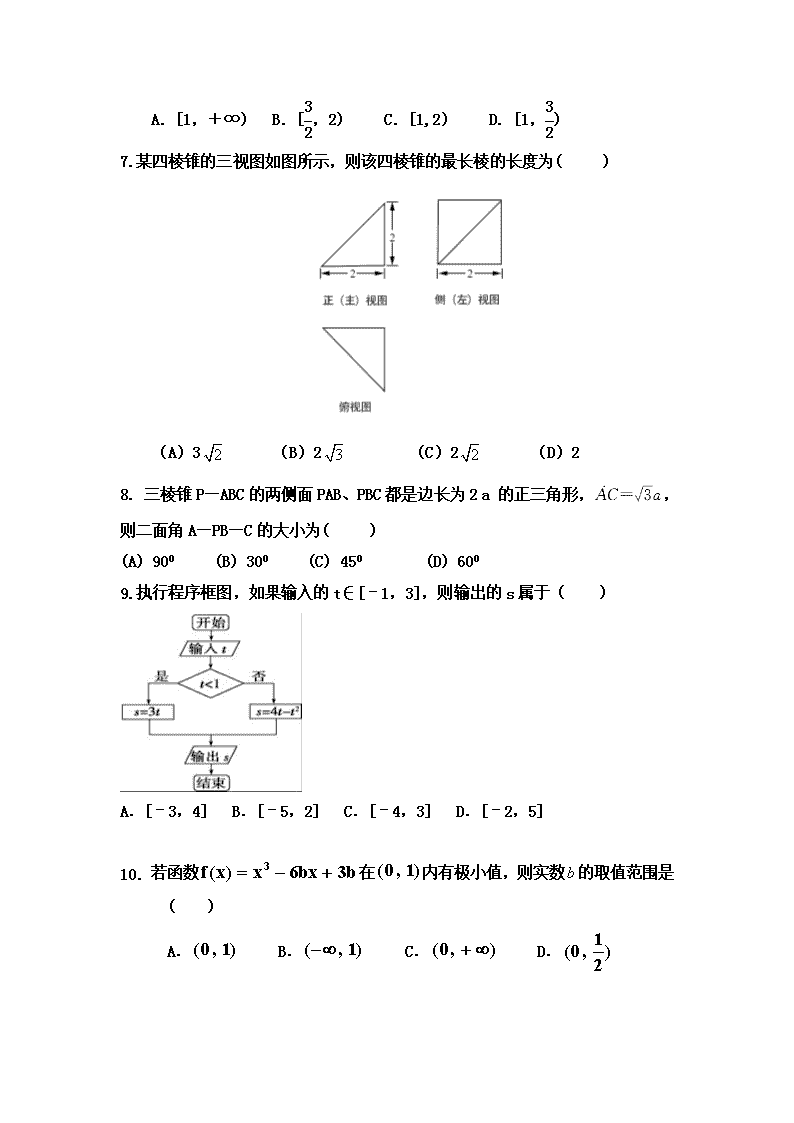
安平中学2017—2018学年上学期期末考试 ‎ ‎ 数学试题 （高二实验文）‎ 考试时间 120分钟 试题分数 150分 ‎ 一、 选择题：（每题只有一个正确选项。共12个小题，每题5分，共60分。‎ ‎1.复数的实部与虚部之差为（ ）‎ A．-1 B．‎1 C． D．‎ ‎2. “a = l”是“函数在区间上为增函数”的( )‎ ‎(A)充分不必要条件 （B)必要不充分条件 ‎(C)充要条件 (D)既不充分也不必要条件 ‎3.若复数（1–i）（a+i）在复平面内对应的点在第二象限，则实数a的取值范围是( )‎ ‎（A）（–∞，1）（B）（–∞，–1）（C）（1，+∞）（D）（–1，+∞）‎ ‎4.下列四个命题中，正确的是（ ）‎ A．若，则 B．若，则 ‎ C.若，则 D．若，则 ‎ ‎5.某产品在某零售摊位的零售价x（单位：元）与每天的销售量y（单位：个）的统计资料如表所示：‎ ‎ x ‎ 16‎ ‎ 17‎ ‎ 18‎ ‎ 19‎ ‎ y ‎ 50‎ ‎ 34‎ ‎ 41‎ ‎ 31‎ 由表可得回归直线方程=x+中的=﹣4，据此模型预测零售价为20元时，每天的销售量为　　　（　　）‎ A．26个 B．27个 C．28个 D．29个 ‎6．若函数在其定义域内的一个子区间(k－1，k＋1)内不是单调函数，则实数k的取值范围是( 　)‎ A． ‎[1，＋∞) B．[，2) C．[1,2) D．[1，) ‎ ‎7.某四棱锥的三视图如图所示，则该四棱锥的最长棱的长度为( 　)‎ ‎（A）3 （B）2 （C）2 （D）2‎ ‎8. 三棱锥P—ABC的两侧面PAB、PBC都是边长为‎2a的正三角形，，则二面角A—PB—C的大小为( 　)‎ ‎(A) 900 (B) 300 (C) 450 (D) 600‎ ‎9.执行程序框图，如果输入的t∈[﹣1，3]，则输出的s属于（　　）‎ A．[﹣3，4] B．[﹣5，2] C．[﹣4，3] D．[﹣2，5]‎ 10． 若函数在内有极小值，则实数的取值范围是( ) ‎ ‎ A． B． C． D．‎ ‎11.设双曲线的左、右焦点分别为，过作轴的垂线与双曲线在第一象限的交点为，已知，点是双曲线右支上的动点，且恒成立，则双曲线的离心率的取值范围是（ ）‎ A． B． C. D．‎ ‎12.已知函数的导数为，且对恒成立，则下列不等式一定成立的是（ ）‎ A． B． C. D．‎ 二. 填空题（共4个小题，每题5分，共20分。）‎ ‎13．某乡镇供电所为了调查农村居民用电量情况，随机抽取了500户居民去年的用电量（单位：kw/h），将所得数据整理后，画出频率分布直方图如图所示；其中直方图从左到右前3个小矩形的面积之比为1：2：3．该乡镇月均用电量在37～39之内的居民共有　　　　户．‎ 14. 在[﹣1，1]上任取一数a，在[1，2]上任取一数b，则点（a，b）满足 a2+b2≤2的概率为 .‎ ‎15.已知整数的数对列如下:‎ ‎(1,1),(1,2),(2,1),(1,3),(2,2),(3,1),(1,4),(2,3),‎ ‎(3,2),(4,1),(1,5), (2,4),…‎ 则第60个数对是 .‎ ‎16.现有一个关于平面图形的命题：如图所示，同一个平面内有两个边长都是a的正方形，其中一个的某顶点在另一个的中心，则这两个正方形重叠部分的面积恒为.类比到空间，有两个棱长均为a的正方体，其中一个的某顶点在另一个的中心，则这两个正方体重叠部分的体积恒为 .‎ ‎ ‎ ‎ ‎ 一、 解答题：（解答题应写出必要的文字说明和演算步骤） ‎ 17． ‎（本小题满分10分）‎ 已知函数，其中．‎ ‎（Ⅰ）当时，求曲线在点处的切线方程；‎ ‎（Ⅱ）当时，求函数的单调区间．‎ ‎18．（本小题满分12分）某高校经济管理学院在‎2014年11月11日“双11购物节”期间，对[25，55]岁的人群随机抽取了100人进行调查，得到各年龄段人数频率分布直方图．同时对这100人是否参加“商品抢购”进行统计，结果如下表：‎ ‎（1）求统计表中a和p的值；‎ ‎（2）从年龄落在（40，50]内的参加“商品抢购”的人群中，采用分层抽样法抽取6人参加满意度调查，在抽取的6人中，有随机的2人感到“满意”，设感到“满意”的2人中年龄在（40，45]内的人数为X，求X的分布列和数学期望．‎ ‎（3）通过有没有95%的把握认为，进行“商品抢购”与“年龄低于40岁”有关？说明你的理由．‎ 组数 分组 抢购商品的人数 占本组的频率 第一组 ‎[25，30）‎ ‎12‎ ‎0.6‎ 第二组 ‎[30，35）‎ ‎18‎ p 第三组 ‎[35，40）‎ ‎10‎ ‎0.5‎ 第四组 ‎[40，45）‎ a ‎0.4‎ 第五组 ‎[45，50）‎ ‎3‎ ‎0.3‎ 第六组 ‎[50，55）‎ ‎1‎ ‎0.2‎ 附：K2=‎ P（χ2≥k）‎ ‎0.100‎ ‎0.050‎ ‎0.010‎ ‎0.001‎ k ‎2.706‎ ‎3.841‎ ‎6.635‎ ‎10.828‎ ‎19.（本小题满分12分）如图，在四棱锥中，平面，，，，，，.‎ ‎（I）求异面直线与所成角的余弦值；‎ ‎（II）求证：平面；‎ ‎（Ⅲ）求直线与平面所成角的正弦值.‎ ‎20.（本小题满分12分）‎ 已知抛物线C：y2=2px过点P（1，1）.过点（0，）作直线l与抛物线C交于不同的两点M，N，过点M作x轴的垂线分别与直线OP，ON交于点A，B，其中O为原点.‎ ‎（Ⅰ）求抛物线C的方程，并求其焦点坐标和准线方程；‎ ‎（Ⅱ）求证：A为线段BM的中点.‎ 21. ‎（本题满分12分）‎ 已知函数f（x）=excosx−x.‎ ‎（Ⅰ）求曲线y= f（x）在点（0，f（0））处的切线方程；‎ ‎（Ⅱ）求函数f（x）在区间[0，]上的最大值和最小值.‎ 21. ‎（本题满分12分）‎ ‎ 已知分别是焦距为的椭圆的左、右顶点，为椭圆上非顶点的点，直线的斜率分别为，且.‎ ‎（1）求椭圆的方程；‎ ‎（2）直线（与轴不重合）过点且与椭圆交于两点，直线与交于点，试求点的轨迹是否是垂直轴的直线，若是，则求出点的轨迹方程，若不是，请说明理由.‎ 高二(实验)文班数学答案 BABCD DBDAD AA ‎13. 125 14. 15.(5,7) 16. ‎ ‎17.（本题满分10分）‎ ‎（Ⅰ）当时，，，‎ 又，．‎ 所以，曲线在点处的切线方程为，‎ 即．‎ ‎（Ⅱ）．‎ 由于，以下分两种情况讨论：‎ ‎（1）当时，令，得到，．当变化时，的变化情况如下表：‎ ‎0‎ ‎0‎ 极小值 极大值 所以在区间，内为减函数，在区间内为增函数． ‎ ‎（2）当时，令，得到，当变化时，的变化情况如下表：‎ ‎0‎ ‎0‎ 极大值 极小值 所以在区间，内为增函数，在区间内为减函数．‎ ‎18.（本题满分12分）‎ 解：（1）因为总人数为100，‎ 所以在[40，45）岁的人数为100×5×0.03=15，‎ 所以a=15×0.4=6；‎ 因为年龄在[30，35）岁的人数的频率为 ‎1﹣5×（0.04+0.04+0.03+0.02+0.01）=0.3，‎ 所以年龄在[30，35）岁的人数为100×0.3=30，‎ 所以p==0.6；‎ ‎（2）依题意，抽取年龄在[40，45）岁之间4人，抽取年龄在[45，50）岁之间2人，‎ X可以取0，1，2；‎ P（X=0）==，P（X=1）==，P（X=2）==；‎ 所以X的分布列为 X ‎0‎ ‎1‎ ‎2‎ P 所以E（X）=0×+1×+2×=；‎ ‎（3）可得2×2列联表为 年龄在40以下 年龄不在40以下 合计 参加抢购 ‎40‎ ‎10‎ ‎50‎ 未参加抢购 ‎30‎ ‎20‎ ‎50‎ 合计 ‎70‎ ‎30‎ ‎100‎ 计算K2=，‎ 因此有95%的把握认为，进行“商品抢购”与“年龄低于40岁”有关．‎ ‎　19.（本题满分12分）（Ⅰ）解：如图，由已知AD//BC，故或其补角即为异面直线AP与BC所成的角.因为AD⊥平面PDC，所以AD⊥PD.在Rt△PDA中，由已知，得，故.‎ 所以，异面直线AP与BC所成角的余弦值为.‎ ‎（Ⅱ）证明：因为AD⊥平面PDC，直线PD平面PDC，所以AD⊥PD.又因为BC//AD，所以PD⊥BC，又PD⊥PB，所以PD⊥平面PBC.‎ ‎（Ⅲ）解：过点D作AB的平行线交BC于点F，连结PF，则DF与平面PBC所成的角等于AB与平面PBC所成的角.‎ 因为PD⊥平面PBC，故PF为DF在平面PBC上的射影，所以为直线DF和平面PBC所成的角.‎ 由于AD//BC，DF//AB，故BF=AD=1，由已知，得CF=BC–BF=2.又AD⊥DC，故BC⊥DC，在Rt△DCF中，可得,在Rt△DPF中，可得.‎ 所以，直线AB与平面PBC所成角的正弦值为. ‎ ‎20（本题满分12分）解：（Ⅰ）由抛物线C：过点P（1，1），得.‎ 所以抛物线C的方程为.‎ 抛物线C的焦点坐标为（，0），准线方程为.‎ ‎（Ⅱ）由题意，设直线l的方程为（），l与抛物线C的交点为，.‎ 由，得.则，.‎ 因为点P的坐标为（1，1），所以直线OP的方程为，点A的坐标为.‎ 直线ON的方程为，点B的坐标为.‎ 因为 ‎，‎ 所以.故A为线段BM的中点.‎ ‎21（本题满分12分）　‎ 解：（Ⅰ）因为，所以.‎ 又因为，所以曲线在点处的切线方程为.‎ ‎（Ⅱ）设，则 ‎.‎ 当时，，‎ 所以在区间上单调递减.‎ 所以对任意有，即.‎ 所以函数在区间上单调递减.‎ 因此在区间上的最大值为，最小值为.‎ ‎22.（本题满分12分）解：（1）设为椭圆上非顶点的点，，又 ‎，即，‎ ‎，故椭圆的方程为.‎ ‎（2）当过点直线斜率不存在时，不妨设，直线的方程是，直线的方程是，交点为.若，由对称性可知交点为.‎ 点在直线上，‎ 当直线斜率存在时，设的方程为，‎ 由得，‎ 记，则.‎ 的方程是的方程是，‎ 得，‎ 即 ‎.‎ 综上所述，点的轨迹方程为.‎