数学（文）卷·2018届河南省西平县高级中学高二下学期第二次月考（2017-03）

数学（文）卷·2018届河南省西平县高级中学高二下学期第二次月考（2017-03）

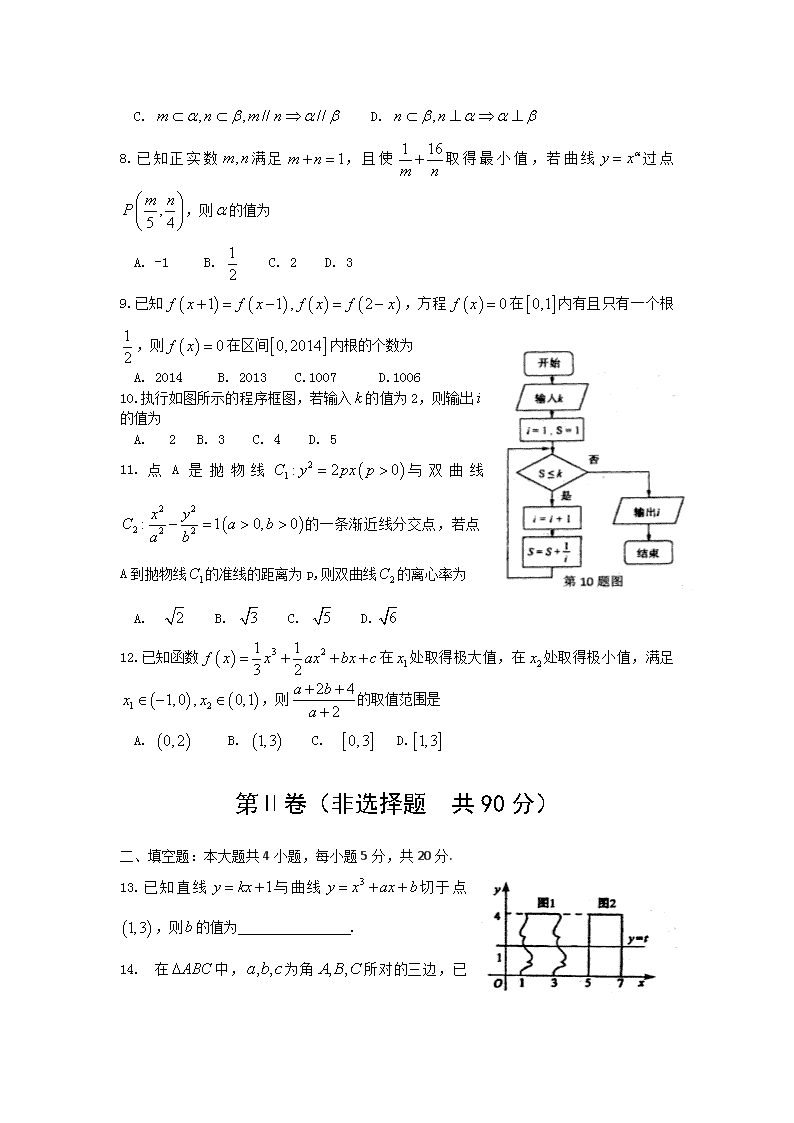
‎】2016—2017学年高二下期第二次月考 数学（文科）‎ 第Ⅰ卷（选择题 共60分）‎ 一、选择题：本大题共12小题，每小题5分，共60分.在每个小题给出的四个选项中，有且只有一项符合题目要求.‎ ‎1.设为虚数单位，则复数对应的点位于 ‎ A. 第一象限 B. 第二象限 C. 第三象限 D.第四象限 ‎2.平面向量与的夹角为，则等于 ‎ A. B. C. 12 D. ‎ ‎3.已知，函数与函数的图象可能是 ‎4.已知命题：对于,恒有成立，命题奇函数的图象必过原点，则下列结论正确的是 ‎ A. 为真 B. 为真 C. 为真 D. 为真 ‎5.已知实数满足，则的最小值为 ‎ A. -4 B. -3 C. 0 D. 1‎ ‎6.一个几何体的三视图如图所示，其中主（正）视图是边长为2的等边三角形，俯视图是正方形，那么该几何体的左（侧）视图面积时 ‎ A. B. C. 4 D. 2‎ ‎7.已知是不同的直线，是不同的平面，则下列说法正确的是 ‎ A. B. ‎ ‎ C. D. ‎ ‎8.已知正实数满足，且使取得最小值，若曲线过点，则的值为 ‎ A. -1 B. C. 2 D. 3‎ ‎9.已知，方程在内有且只有一个根，则在区间内根的个数为 ‎ A. 2014 B. 2013 C.1007 D.1006‎ ‎10.执行如图所示的程序框图，若输入的值为2，则输出的值为 ‎ A. 2 B. 3 C. 4 D. 5‎ ‎11.点A是抛物线与双曲线的一条渐近线分交点，若点A到抛物线的准线的距离为p,则双曲线的离心率为 ‎ A. B. C. D.‎ ‎12.已知函数在处取得极大值，在处取得极小值，满足，则的取值范围是 ‎ A. B. C. D.‎ 第Ⅱ卷（非选择题 共90分）‎ 二、填空题：本大题共4小题，每小题5分，共20分.‎ ‎13.已知直线与曲线切于点，则的值为 .‎ ‎14.在中，为角 所对的三边，已知，，则 .‎ ‎15.我国南北朝时期的数学家祖恒提出体积的计算原理（祖恒原理）“幂势既同，则积不容异”.“势”即是高，“幂”是面积.意思是：如果两等高的几何体在同高处截得两几何体的截面积恒等，那么这两个几何体的体积相等.类比祖恒原理，如图所示，在平面直角坐标系中，图1是一个形状不规则的封闭图形，图2是一个矩形，且当实数取上的任意值时，直线被图1和图2所截得的两线段长始终相等，则图1的面积为 . ‎ ‎16.在平面直角坐标系中，已知点在曲线上，点在直线上，则的最小值为 .‎ 三、解答题：本大题共6小题，共70分.解答应写出必要的文字说明或推理、验算过程.‎ ‎17.（本题满分12分）‎ ‎ 已知等差数列满足，数列的前项和为，且满足 ‎ （1）求数列，的通项公式；‎ ‎ （2）数列满足，求数列的前项和.‎ ‎18.（本题满分12分）如图，在四棱锥中，底面是正方形，底面，,点是的中点，,且交于点 ‎ （1）求证：平面；‎ ‎ （2）求点到平面的距离.‎ ‎19.（本题满分12分）‎ ‎ 某中学一位高三班主任对本班的50名学生学习积极性和对待班级工作的态度进行调查，得到的统计数据如下表所示：‎ ‎（1）如果随机调查这个班的一名学生，那么抽到不积极参加班级工作且学习积极性不高的学生的概率是多少？‎ ‎ （2）若不积极参加班级工作且学习积极性高的7名学生中有两名男生，现从中抽取2名学生参加某项活动，问两名学生中有1名男生的概率是多少？‎ ‎（3）学生的学习积极性与对待班级工作的态度是否有关系？请说明理由.‎ ‎20.（本题满分12分）已知椭圆上任意一点到两焦点距离之和为，离心率为 ‎ （1）求椭圆的标准方程；‎ ‎ （2）若直线的斜率为，直线与椭圆C交于A,B两点，点为椭圆上一点，求的面积的最大值.‎ ‎.‎ ‎21.（本题满分12分）已知函数 ‎ （1）若是的极值点，求的极大值；‎ ‎ （2）求的范围，使得恒成立 ‎22.（本题满分10分）选修4-4：参数方程与极坐标系 ‎ 在平面直角坐标系中，曲线的参数方程为（为参数），以坐标原点O为极点，轴的正半轴为极轴的极坐标系中，曲线的极坐标方程为, 曲线 ‎（1）求曲线与曲线交点M的直角坐标；‎ ‎（2）设点A,B分别是曲线曲线， 上的动点，求的最小值.‎