2019届二轮复习1-2集合的运算课件（17张）（全国通用）

2019届二轮复习1-2集合的运算课件（17张）（全国通用）

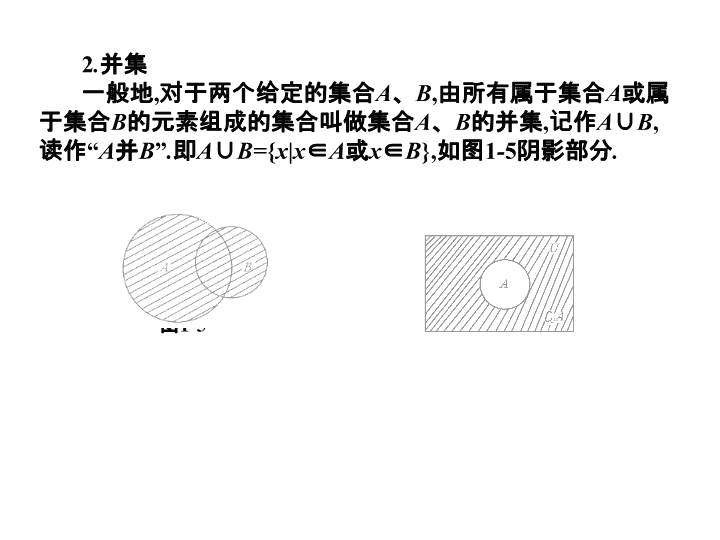
1.2 集合的运算 【考纲要求】　理解全集、交集、并集、补集的概念 . 【学习重点】　求交集、并集、补集 . 一、自主学习 ( 一 ) 知识归纳 1 . 交集 一般地 , 对于两个给定的集合 A 、 B , 由所有既属于集合 A 且属于集合 B 的元素组成的集合叫做集合 A 、 B 的交集 , 记作 A ∩ B , 读作 “ A 交 B ” . 即 A ∩ B= { x|x ∈ A 且 x ∈ B }, 如图 1 - 4 阴影部分 . 图 1 - 4 2 . 并集 一般地 , 对于两个给定的集合 A 、 B , 由所有属于集合 A 或属于集合 B 的元素组成的集合叫做集合 A 、 B 的并集 , 记作 A ∪ B , 读作 “ A 并 B ” . 即 A ∪ B= { x|x ∈ A 或 x ∈ B }, 如图 1 - 5 阴影部分 . 图 1 - 5 图 1 - 6 3 . 补集 我们在研究集合与集合之间的关系时 , 如果一些集合都是某一给定集合的子集 , 那么称这个给定的集合为这些集合的全集 , 通常用 U 表示 . 如果没有特别说明 , 我们通常把实数集 R 看作全集 . 一般地 , 设 U 是全集 ,A 是 U 的一个子集 ( 即 A⊆U), 由集合 U 中不属于集合 A 的所有元素组成的集合 , 叫做 A 在 U 中的补集 , 记作 ∁ U A, 读作 “ 集合 A 在集合 U 中的补集 ” . 即 ∁ U A={x|x∈U 且 x∉A}, 如图 1-6 阴影部分 . 4 . 集合运算的性质 一般地 , 我们把求交集、并集及补集的过程叫集合的运算 . (1) A ⊆ B ⇔ A ∩ B=A ⇔ A ∪ B=B. (2) A ∩(∁ U A ) = ∅, A ∪(∁ U A ) =U ,∁ U (∁ U A ) =A. (3) 德 · 摩根法则 : (∁ U A )∩(∁ U B ) = ∁ U ( A ∪ B ),(∁ U A )∪(∁ U B ) = ∁ U ( A ∩ B ) . ( 二 ) 基础训练 1 . 已知集合 A= {1,2,4}, B= {2,3,5}, 求 A ∩ B , A ∪ B. 解 :∵ A= {1,2,4}, B= {2,3,5} 　 ∴ A ∩ B= {2}, A ∪ B= {1,2,3,4,5} . 2 . 设集合 A= {8 的约数 }, B= {3,4,7,8,9}, 求 A ∩ B. 解 :∵ A= {8 的约数 }, B= {3,4,7,8,9} 　 ∴ A ∩ B= {4,8} . 3 . 设集合 A= {( x , y ) |x+ 2 y= 2}, B= {( x , y ) | 3 x-y= 13}, 则 A ∩ B= ( 　 ) A.( - 4,1) B.{( - 4,1)} C.(4, - 1) D.{(4, - 1)} 4 . (1) 若 U= { 小于 8 的正整数 }, A= {2,3,4}, 求 ∁ U A ; (2) 设 U= R, A= { x|x< 1}, 求 ∁ U A. 【 答案 】D 　 ∵ A= {( x , y ) |x+ 2 y= 2}, B= {( x , y ) | 3 x-y= 13} ∴ A ∩ B= {(4, - 1)}, 选 D . 解 :(1)∵ U= {1,2,3,4,5,6,7}, A= {2,3,4} 　 ∴∁ U A= {1,5,6,7} . 　 (2) ∵U= R, A= { x|x< 1} 　 ∴∁ U A= { x|x ≥1} . 二、探究提高 【例 1 】　 (1) 已知全集 U= {1,2,3,4,5,6}, 集合 M= {1,2,3,4}, 集合 N= {2,4,6}, 则 N ∩(∁ U M ) = ( 　　 ) A.{1,3} B.{1,2,3,4,5} C.{6} D.{1,2,3,4,6} 分析 : 先求 ∁ U M , 再求它与 N 的交集 . (2) 设 A= {( x , y ) |y=x+ 3}, B= {( x , y ) |y=- 2 x+ 6}, 求 A ∩ B. 【解】　 ∁ U M= {5,6}, N ∩(∁ U M ) = {6}, 答案为 C. 【小结】　注意从不同的角度理解交集、并集、补集的含义 ( 见下表 ): 形式 用列举法表示 用描述法表示 用韦恩图表示 A ∩ B 找公共元素 同时满足两个集合的限制条件 找公共部分 A ∪ B 找所有元素 至少满足一个集合的限制条件 找所有部分 ∁ U A 找剩余元素 满足全集条件 , 但不满足 A 的限制条件 找剩余部分 【例 2 】　已知集合 M= { x| 0 2}, B= { x| 0 0} B.{ x|x ≠2} C.{ x|x> 0 或 x ≠2} D.{ x|x> 0 且 x ≠2} 【 答案 】D 【 答案 】A 【 答案 】D 7 . 设集合 M= { x|x 2 = 1}, N= {0,1}, 则 M ∪ N= 　　　　　 .  8 . 已知全集 U= { x|- 5 3}, B= { x| 2

查看更多