- 2021-06-21 发布 |
- 37.5 KB |
- 4页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
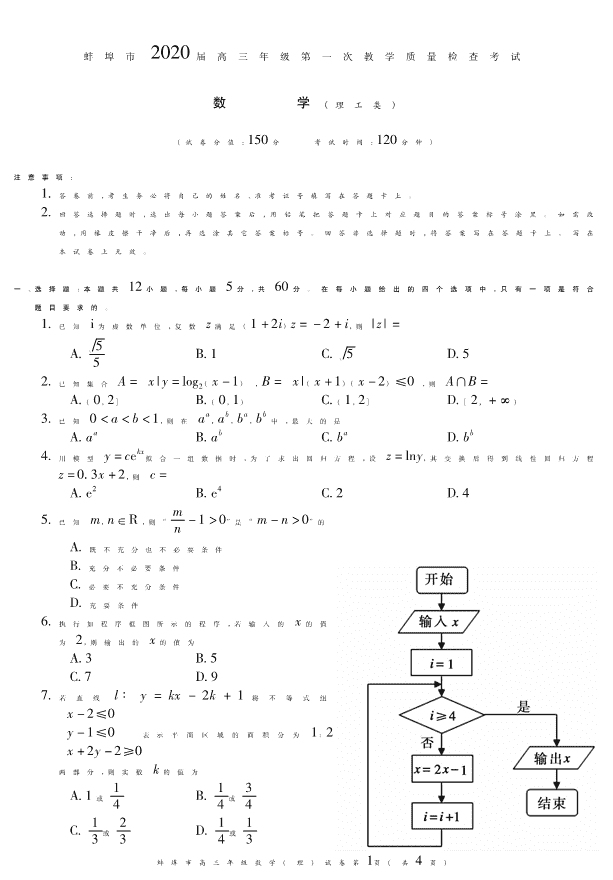
安徽省蚌埠市2020届高三9月第一次教学质量检查(理)试题
书书书 蚌埠市 2020届高三年级第一次教学质量检查考试 数 学(理工类) (试卷分值:150分 考试时间:120分钟) 注意事项: 1答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。 2回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改 动,用橡皮擦干净后,再选涂其它答案标号。回答非选择题时,将答案写在答题卡上。写在 本试卷上无效。 一、选择题:本题共 12小题,每小题 5分,共 60分。在每小题给出的四个选项中,只有一项是符合 题目要求的。 1已知 i为虚数单位,复数 z满足(1+2i)z=-2+i,则|z|= A槡5 5 槡B1 C 5 D5 2已知集合 A= x|y=log2(x-1{ }),B= x|(x+1)(x-2)≤{ }0,则 A∩B= A(0,2] B(0,1) C(1,2] D[2,+∞) 3已知 0<a<b<1,则在 aa,ab,ba,bb中,最大的是 Aaa Bab Cba Dbb 4用模型 y=cekx拟合一组数据时,为了求出回归方程,设 z=lny,其变换后得到线性回归方程 z=03x+2,则 c= Ae2 Be4 C2 D4 5已知 m,n∈R,则“m n-1>0”是“m-n>0”的 A既不充分也不必要条件 B充分不必要条件 C必要不充分条件 D充要条件 6执行如程序框图所示的程序,若输入的 x的值 为 2,则输出的 x的值为 A3 B5 C7 D9 7若 直 线 l∶ y=kx-2k+1将 不 等 式 组 x-2≤0 y-1≤0 x+2y-2≥{ 0 表示平面区域的面积分为 1:2 两部分,则实数 k的值为 A1或 1 4 B1 4或 3 4 C1 3或 2 3 D1 4或 1 3 )页4共(页1第卷试)理(学数级年三高市埠蚌 8定积分2 -2 ( 4-x槡 2 -sinx+x3)dx的值是 Aπ B2π C2π+2cos2 Dπ+2cos2 9已知三棱锥 P-ABC的所有顶点都在球 O的球面上,PA⊥平面 ABC,AB=AC=2,∠BAC= 120°,若三棱锥 P-ABC的体积为 槡23 3 ,则球 O的表面积为 A16π B20π C28π D32π 10已知椭圆 C∶x2 a2 +y2 b2 =1(a>b>0)的焦距为 槡23,椭圆 C与圆(x 槡+ 3)2+y2=16交于 M, N两点,且|MN|=4,则椭圆 C的方程为 Ax2 15+y2 12=1 Bx2 12+y2 9=1 Cx2 6+y2 3=1 Dx2 9+y2 6=1 11已知函数 f(x)=asinx+cosx,x∈ 0,π( )6 ,若x1≠x2,使得 f(x1)=f(x2),则实数 a的取值 范围是 A0,槡3( )2 B(0,槡3) C槡3 3,槡( )3 D0,槡3( )3 12已知棱长为 1的正方体 ABCD-A1B1C1D1,点 P是四边形 BB1D1D内(含边界)任意一点, Q是 B1C1中点,有下列四个结论: ①AC⊥BP =0;②当 P点为 B1D1中点时,二面角 P-AD-C的余弦值 1 2;③AQ与 BC所成 角的正切值为 槡22;④当 CQ⊥AP时,点 P的轨迹长为 3 2 其中所有正确的结论序号是 A①②③ B①③④ C②③④ D①②④ 二、填空题:本题共 4小题,每小题 5分,共 20分。 13已知平面向量a=(-3,4)与 A(1,m),B(2,1),且a∥AB,则实数 m的值为 14已知定义在R上的奇函数 f(x),对任意 x都满足 f(x+2)=f(4-x),且当 x∈[0,3], f(x)=log2(x+1),则 f(2019)= 15蚌埠市大力发展旅游产业,蚌埠龙子湖风景区、博物馆、张公山公园、花鼓灯嘉年华、禾泉 农庄、淮河闸水利风景区都是 4A风景区,还有荆涂山风景区、大明御温泉水世界、花博园 等也都是不错的景点,小明和朋友决定利用三天时间从以上 9个景点中选择 6个景点游 玩,每个景点用半天(上午、下午各游玩一个景点),且至少选择 4个 4A风景区,则小明这 三天的游玩有 种不同的安排方式 (用数字表示) 16已知 f(x)= x2 x≤0 ex-2 x{ >0 ,若方程 f(x)=m(m∈R)恰有两个实根 x1,x2,则 x1 +x2 的最 大值是 )页4共(页2第卷试)理(学数级年三高市埠蚌 三、解答题:共 70分。解答应写出文字说明、证明过程或演算步骤。 17(10分) 在△ABC中,角 A,B,C的对边分别为 a,b,c,若 cos(A-B)=4 5,且 A<B,tanB=4 3. (1)求 tanA; (2)若 b=2,求△ABC的周长 18(12分) 设数列{an}的前 n项和为 Sn,满足 Sn-2Sn-1=n (n≥2,n∈N ),且 a1=1 (1)求证:数列{an+1}是等比数列; (2)若 bn=log2(an+1)an+1,求数列{bn}的前 n项和 Tn 19(12分) 如图所示,在四棱锥 P-ABCD中,AD∥BC,BC⊥平面 PAB,PB=PA=AB=BC=2AD=2,E 为线段 PB的中点 第 19题图 (1)证明:AE∥平面 PDC; (2)求直线 DE与平面 PDC所成角的正弦值 )页4共(页3第卷试)理(学数级年三高市埠蚌 20(12分) 某高铁站停车场针对小型机动车收费标准如下:2小时内(含 2小时),每辆每次收费 5 元;超过 2小时不超过 5小时,每增加一小时收费增加 3元,不足一小时的按一小时计费; 超过 5小时至 24小时内(含 24小时)收费 15元封顶。超过 24小时,按前述标准重新计 费 为了调查该停车场一天的收费情况,现统计 1000辆车的停留时间(假设每辆车一天 内在该停车场仅停车一次),得到下面的频数分布表: T(小时) (0,2] (2,3] (3,4] (4,5] (5,24] 频数(车次) 600 120 80 100 100 以车辆在停车场停留时间位于各区间的频率代替车辆在停车场停留时间位于各区间的概 率。 (1)X表示某辆车在该停车场停车一次所交费用,求 X的概率分布列及期望 E(X); (2)现随机抽取该停车场内停放的 3辆车,ξ表示 3辆车中停车费用少于 E(X)的车辆数, 求 P(ξ≥2)的概率 21(12分) 已知点 A,B是抛物线 C:y2=2px(p>0)上关于 x轴对称的两点,点 E是抛物线 C的准线 与 x轴的交点 (1)若△EAB是面积为 4的直角三角形,求抛物线 C的方程; (2)若直线 BE与抛物线 C交于另一点 D,证明:直线 AD过定点 22(12分) 已知函数 f(x)=alnx x ,g(x)=aex-a-1,且 y=x-1是曲线 y=f(x)的切线 (1)求实数 a的值以及切点坐标; (2)求证:g(x)≥f(x) )页4共(页4第卷试)理(学数级年三高市埠蚌查看更多