2019-2020学年四川省南充高级中学高二上学期期中考试数学（理）试题 word版

2019-2020学年四川省南充高级中学高二上学期期中考试数学（理）试题 word版

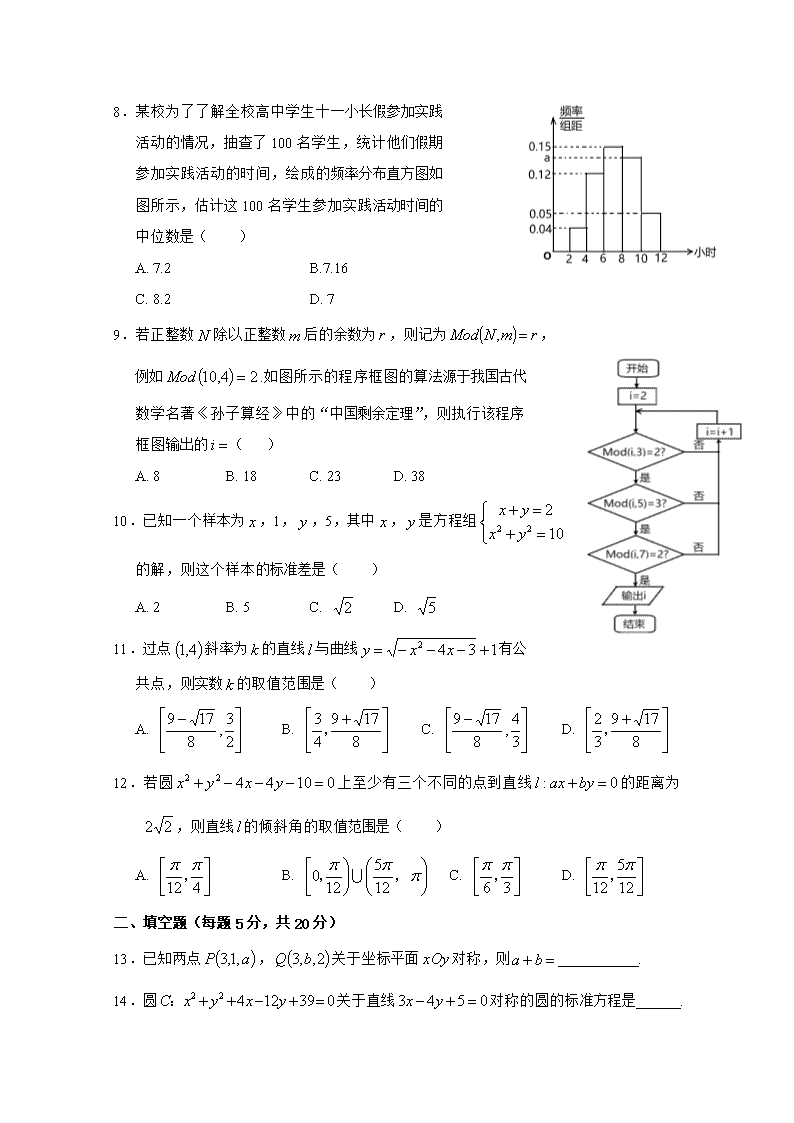
南充高中2019－2020学年度上学期期中考试 高2018级数学试题（理科）‎ ‎ ‎ 一、选择题（每题5分，共60分）‎ ‎1．某学校有小学生125人，初中生280人，高中生95人，为了调查学生的身体状况，需要从他们当中抽取一个容量为100的样本，采用较恰当的方法是（ ）‎ A. 抽签法 B. 随机数法 C. 系统抽样 D. 分层抽样 ‎ ‎2．下列函数为偶函数的是（ ）‎ A. B. C. D. ‎ ‎3．已知等差数列，若，，则的前7项和等于（ ）‎ A. 112 B. ‎51 ‎ C. 28 D. 18‎ ‎4．已知向量，，若，则实数（ ）‎ A. B. C. 3 D. ‎ ‎5．右图是一个边长为4的正方形二维码，为了测算图中黑色部分的面积，‎ 在正方形区域内随机投掷400个点，其中落入黑色部分的有225个点，‎ 据此可以估计黑色部分的面积为（ ）‎ A. 8 B. ‎9 ‎ C. 10 D. 12‎ ‎6．袋中装有白球3个，黑球4个，从中任取3个，下列各对事件中互为对立事件的是（ ）‎ A. 恰有1个白球和全是白球 B. 至少有1个白球和全是黑球 C. 至少有1个白球和至少有2个白球 D. 至少有1个白球和至少有1个黑球 甲 乙 ‎8‎ ‎9‎ ‎7‎ ‎6‎ ‎5‎ x ‎3‎ ‎8‎ ‎1‎ ‎2‎ y ‎6‎ ‎2‎ ‎9‎ ‎1‎ ‎1‎ ‎6‎ ‎7．某中学从甲、乙两个班中各选出7名学生参加数学竞赛，‎ 他们取得的成绩（满分100分）的茎叶图如图所示，其中 甲班学生成绩的众数是83，乙班学生成绩的平均数是 ‎86，‎ 则的值为（ ）‎ A. 7 B. ‎8 C. 9 D. 10‎ ‎8．某校为了了解全校高中学生十一小长假参加实践 活动的情况，抽查了100名学生，统计他们假期 参加实践活动的时间，绘成的频率分布直方图如 图所示，估计这100名学生参加实践活动时间的 中位数是（ ） ‎ A. 7.2‎‎ B.7.16 ‎ C. 8.2 D. 7‎ ‎9．若正整数除以正整数后的余数为，则记为，‎ 例如.如图所示的程序框图的算法源于我国古代 数学名著《孙子算经》中的“中国剩余定理”，则执行该程序 框图输出的（ ）‎ A. 8 B. ‎18 ‎ C. 23 D. 38‎ ‎10．已知一个样本为，1，，5，其中，是方程组 的解，则这个样本的标准差是（ ）‎ A. 2 B. ‎5 ‎ C. D. ‎ ‎11．过点斜率为的直线与曲线有公 共点，则实数的取值范围是（ ）‎ A. B. C. D. ‎ ‎12．若圆上至少有三个不同的点到直线的距离为，则直线的倾斜角的取值范围是（ ）‎ A. B. C. D. ‎ 二、填空题（每题5分，共20分）‎ ‎13．已知两点，关于坐标平面对称，则 .‎ ‎14．圆关于直线对称的圆的标准方程是 .‎ ‎15．已知两条直线与平行，则实数 .‎ ‎16．已知、两点分别在两直线，上运动，是 线段的中点，且，则的取值范围是 .‎ 三、 解答题（17题10分，18～22题每题12分）‎ ‎17.（10分）已知圆的方程是 （1） 求实数的取值范围；‎ （2） 若圆与圆外切，求实数的值.‎ ‎18.（12分）南充高中扎实推进阳光体育运动，积极引导学生走向操场，走进大自然，参加体育锻炼，每天上午第三节课后全校大课间活动时长35分钟。现为了了解学生的体育锻炼时间，采用简单随机抽样法抽取了100名学生，对其平均每日参加体育锻炼的时间（单位：分钟）进行调查，按平均每日体育锻炼时间分组统计如下表：‎ 分组 男生人数 ‎2‎ ‎16‎ ‎19‎ ‎18‎ ‎5‎ ‎3‎ 女生人数 ‎3‎ ‎20‎ ‎10‎ ‎2‎ ‎1‎ ‎1‎ 若将平均每日参加体育锻炼的时间不低于120分钟的学生称为“锻炼达人”.‎ （1） 将频率视为概率，估计我校7000名学生中“锻炼达人”有多少?‎ （2） 从这100名学生的“锻炼达人”中按性别分层抽取5人参加某项体育活动.‎ ‎①求男生和女生各抽取了多少人；‎ ‎②若从这5人中随机抽取2人作为组长候选人，求抽取的2人中男生和女生各1人的概率.‎ ‎19.（12分）已知的顶点，边上的中线所在直线方程为 ‎，边上的高所在直线方程为. 求：‎ （1） 直线的斜截式方程；‎ （2） 的面积.‎ ‎20.（12分）随着人们经济收入的不断增加，个人购买家庭轿车已不再是一种时尚。车的使用费用，尤其是随着使用年限的增多，所支出的费用到底会增长多少，一直是购车一族非常关心的问题。某汽车销售公司做了一次抽样调查，并统计得出某款车的使用年限与所支出的总费用（万元）有如表的数据资料：‎ 使用年限 ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ 总费用 ‎2.2‎ ‎3.8‎ ‎5.5‎ ‎6.5‎ ‎7.0‎ （1） 求线性回归方程；‎ （2） 估计使用年限为12年时，使用该款车的总费用是多少万元?‎ 线性回归方程中斜率和截距用最小二乘法估计计算公式如下：‎ ‎21.（12分）如图，为半圆的直径，点为半圆上一点，‎ ‎，平面，为中点，.‎ （1） 求证：；‎ （2） 求直线与平面所成角的正弦值.‎ ‎22.（12分）已知的三顶点坐标分别为...‎ （1） 求的外接圆圆的方程；‎ （1） 已知动点在直线上，过点作圆的两条切线，切点分别 为.‎ ‎①记四边形的面积分别为，求的最小值；‎ ‎②证明直线恒过定点.‎ 高2018级期中考试数学试题（理科）答案 一、 选择题 DBCBB BBACD AD 二、 填空题 13. ‎ 14. 15. 16. ‎ 三、 解答题 17. 解：（1）圆的标准方程是，则 故的取值范围是 （2） 由已知得圆的标准方程是 圆与圆相外切，则圆心距等于半径之和，即 18. 解：（1）由表可知，100名学生中“锻炼达人”的人数为10人，将频率视为概率，我校7000名学生中“锻炼达人”的人数为（人）‎ ‎（2）①由（1）知100名学生中的“锻炼达人”有10人，其中男生8人，女生2人。‎ 从10人中按性别分层抽取5人参加体育活动，则男生抽取4人，女生抽取1人。‎ ‎②抽取的5人中有4名男生和1名女生，四名男生一次编号为男1，男2，男3，男4，则5人中随机抽取2人的所有结果有：男1男2，男1男3，男1 男4，男1女，男2男3，男2男4，男2女，男3男4，男3女，男4女。共有10种结果，且每种结果发生的可能性相等。记“抽取的2人中男生和女生各1人”为事件，则事件包含的结果有男1女，男2女，男3女，男4女，共4个，故。‎ 19. 解：（1）设点，则点，由已知有 故点，同理可得点，故直线的方程为，化为斜截式方程为 ‎（2）由（1）知，直线的一般式方程为 边上的高即点到直线的距离为 17. 解：（1）由表可得 ‎，所求线性回归方程为 ‎（2）当时，，即使用12年的车的总费用大概为14.84万元。‎ ‎21. 解（1）‎ 又故 ‎（2）由（1）知，又，‎ 故 ‎，‎ 作 故是直线所成的角。 ‎ 由题意有 由与相似有，即 又 在中，‎ 故直线与平面所成角的正弦值是。‎ ‎22. 解：（1）设的外接圆圆的标准方程为 ‎，根据题意有 故所求的圆的方程为 ‎（2）①，故当最小时，最小。‎ 的最小值即为点到直线的距离 故 ‎②由圆的切线性质有，则，四点共圆，该圆是以为直径的圆，设圆心为点。点是直线上一动点，设，则圆的方程为 圆与圆相交于点 由消去得直线的方程为 即，令得 故直线恒过定点.‎