数学理卷·2018届黑龙江省伊春市第二中学高二下学期期末考试（2017-07）

数学理卷·2018届黑龙江省伊春市第二中学高二下学期期末考试（2017-07）

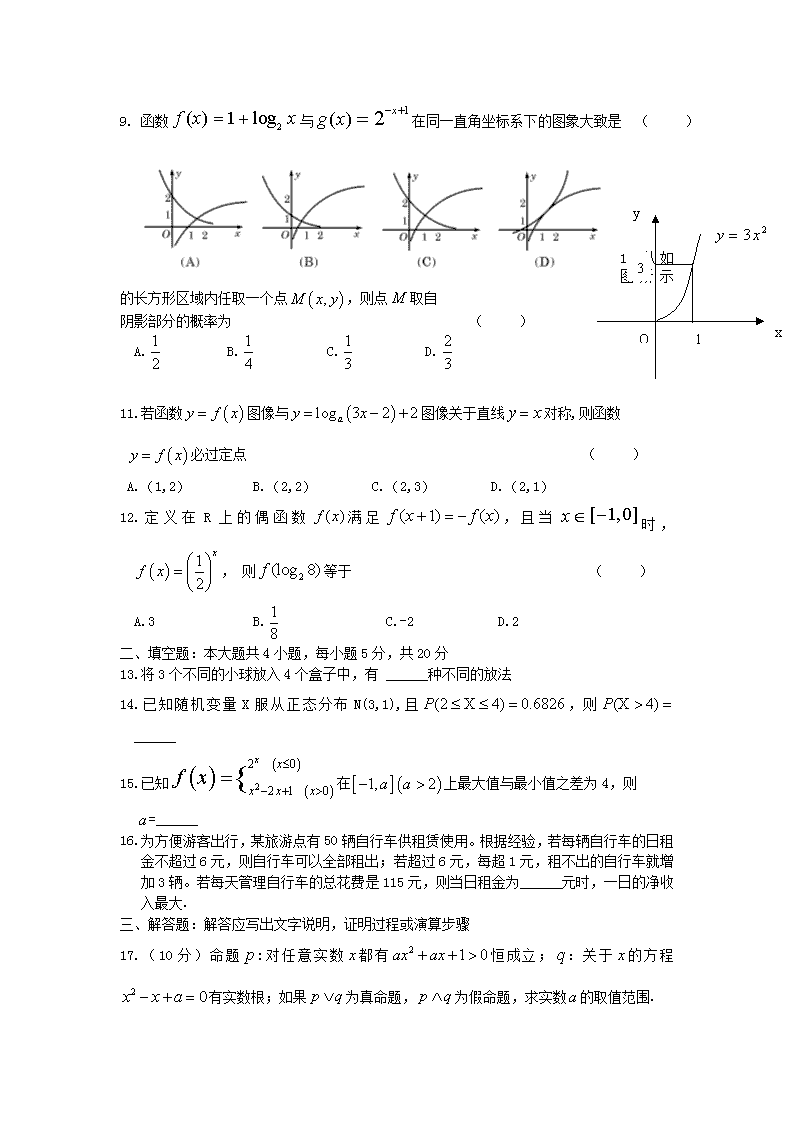
‎2016-2017学年度第二学期期末 高二数学（理）试题 时间：120分钟 分值：150分 一、选择题：本大题共12小题，每小题5分，共60分；在每小题给出的四个选项中，只有一项是符合题目要求的。‎ ‎1.设集合则 （ ） ‎ ‎ A． B. C. D. ‎ ‎2.设集合 ，则 （ ） ‎ A. B. C. D. ‎ ‎3.下列命题中真命题的个数是 （ 　 ）‎ ① ‎ ‎ ② 若 是假命题，则都是假命题 ‎ ‎ ③ 命题“”的否定为“”‎ A．0　　 B．‎1　　‎‎ ‎ C．2　　 D．3 ‎ ‎4.的一个必要不充分条件是 （ ）‎ ‎ A. B. C. D. ‎ ‎5.把一枚硬币任意掷两次，事件A=“第一次出现正面”，事件B=“第二次出现正面”，则P（B/A）= （ ）‎ A. B. C. D.‎ ‎6.方程根的个数为 ( )‎ A.0 B‎.1 ‎‎ C.2 D.3 ‎ ‎7.在的展开式中，常数项是 (　 )‎ A.7 B.‎-7 ‎‎ C.28 D.-28‎ ‎8.设 , , ,则 ( )‎ A. B. C. D.‎ ‎9. 函数与在同一直角坐标系下的图象大致是 （ 　）‎ ‎ ‎ O x y ‎1‎ ‎3‎ ‎ ‎ ‎10.从如图所示的长方形区域内任取一个点，则点取自 阴影部分的概率为 （ ） ‎ A. B. C. D. ‎ ‎11.若函数图像与图像关于直线对称,则函数 必过定点 （ ） A.（1,2） B.（2,2） C.（2,3） D.（2,1）‎ ‎12.定义在R上的偶函数满足，且当时，， 则等于 （ ）‎ A.3 B. C.-2 D.2‎ 二、填空题：本大题共4小题，每小题5分，共20分 ‎13.将3个不同的小球放入4个盒子中，有 ______种不同的放法 ‎14.已知随机变量X服从正态分布N(3,1),且，则 ______‎ ‎15.已知在上最大值与最小值之差为4，则 ‎=______‎ ‎16.为方便游客出行，某旅游点有50辆自行车供租赁使用。根据经验，若每辆自行车的日租金不超过6元，则自行车可以全部租出；若超过6元，每超1元，租不出的自行车就增加3辆。若每天管理自行车的总花费是115元，则当日租金为______元时，一日的净收入最大.‎ 三、解答题：解答应写出文字说明，证明过程或演算步骤 ‎17.（10分）命题:对任意实数都有恒成立；：关于的方程有实数根；如果为真命题，为假命题，求实数的取值范围.‎ ‎18.（12分）某种产品的广告费用支出 与销售额之间有如下的对应数据：‎ ‎（1）求回归直线方程；‎ ‎（2）据此估计广告费用为10时，销售收入的值. ‎ ‎2‎ ‎4‎ ‎5‎ ‎6‎ ‎8‎ ‎30‎ ‎40‎ ‎60‎ ‎50‎ ‎70‎ ‎( 参考公式：用最小二乘法求线性回归方程系数公式)‎ ‎19.（12分）从5名男生和3名女生中任选3人参加奥数训练，设随机变量X表示所选3人中女生的人数 ‎（1）求“所选3人中女生人数X>‎1”‎的概率.‎ ‎（2）求X的分布列及数学期望.‎ ‎20.（12分）调查在级风的海上航行中71名乘客的晕船情况，在男人中有12人晕船，25人不晕船，在女人中有10人晕船，24人不晕船. ‎ ‎（1）作出性别与晕船关系的列联表；‎ 晕船 不晕船 总计 男人 女人 总计 ‎（2）根据此资料，能否在犯错误的概率不超过0.1的前提下认为级风的海上航行中晕船与性别有关？‎ 附：.‎ ‎ ‎ ‎0.25‎ ‎0.15‎ ‎0.10‎ ‎0.05‎ ‎0.025‎ ‎ ‎ ‎1.323‎ ‎2.072‎ ‎2.706‎ ‎3.841‎ ‎5.024‎ ‎21.（12分）已知函数．（）‎ ‎（Ⅰ）当时，求在区间[1，e]上的最大值和最小值；‎ ‎（Ⅱ）求的极值.‎ ‎22.（12分）已知函数 ‎（Ⅰ）若函数在处的切线与直线平行，求的值；‎ ‎（Ⅱ）当时，不等式恒成立，求实数的取值范围．‎ ‎2016—2017学年度第二学期期末高二理科数学试卷答案 一、选择题（共12小题,每小题5分，共60分）‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ B A B B C D A A C C D D 二、填空题（共4小题,每小题5分，共20分）‎ ‎13、64 14、 0.1587 15、 3 16、 11‎ 三、解答题（共6个小题，第17题10分，第18—22题每题12分，共70分，） ‎ ‎17、解：P： 对任意实数x都成立 ‎ 当a=0时，1>0成立，当时， ‎ q:‎ p真q假： p假q真：‎ 则a的取值范围 ‎18、解：(1)＝5，＝50 ；x1y1＋x2y2＋…＋x5y5＝1380‎ a＝－b＝50－6.5×5＝17.5，于是所求的回归直线方程是y＝6.5x＋17.5．‎ ‎(2)当时， ‎ ‎19、解：(1) ‎ ‎(2)X的所有可能取值为0,1,2,3‎ ‎ ‎ X ‎0‎ ‎1‎ ‎2‎ ‎3‎ P ‎ ‎ ‎20解：（1）‎ 晕船 不晕船 总计 男人 ‎12‎ ‎25‎ ‎37‎ 女人 ‎10‎ ‎24‎ ‎34‎ 总计 ‎22‎ ‎49‎ ‎71‎ ‎（2）由公式得χ2＝＝≈0.08.‎ ‎∵χ2<2.706.‎ ‎∴不能在犯错误的概率不超过0.1的前提下认为级风的海上航行中晕船与性别有关．‎ ‎21 、解：（Ⅰ）当时，， ‎ 对于[1，e]，有，∴在区间[1，e]上为增函数， ‎ ‎∴，．-----4分 ‎ （Ⅱ）（x>0）‎ ‎①当，即时，‎ ‎ ，所以，在（0，+∞）是单调递增函数,故无极值点。‎ ‎②当，即时 ‎ 令，得（舍去）‎ ‎ 当变化时，的变化情况如下表：‎ ‎+‎ ‎0‎ ‎-‎ ‎ 由上表可知，时， …………12分 ‎22 、（Ⅰ） 则=3，所以a=-1‎ ‎（Ⅱ）不等式可化为 ‎，‎ 令，则问题可化为 要使上式成立，只需要是增函数即可 即在上恒成立，即在上恒成立，故 则实数a的取值范围是