- 2021-06-20 发布 |
- 37.5 KB |
- 15页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
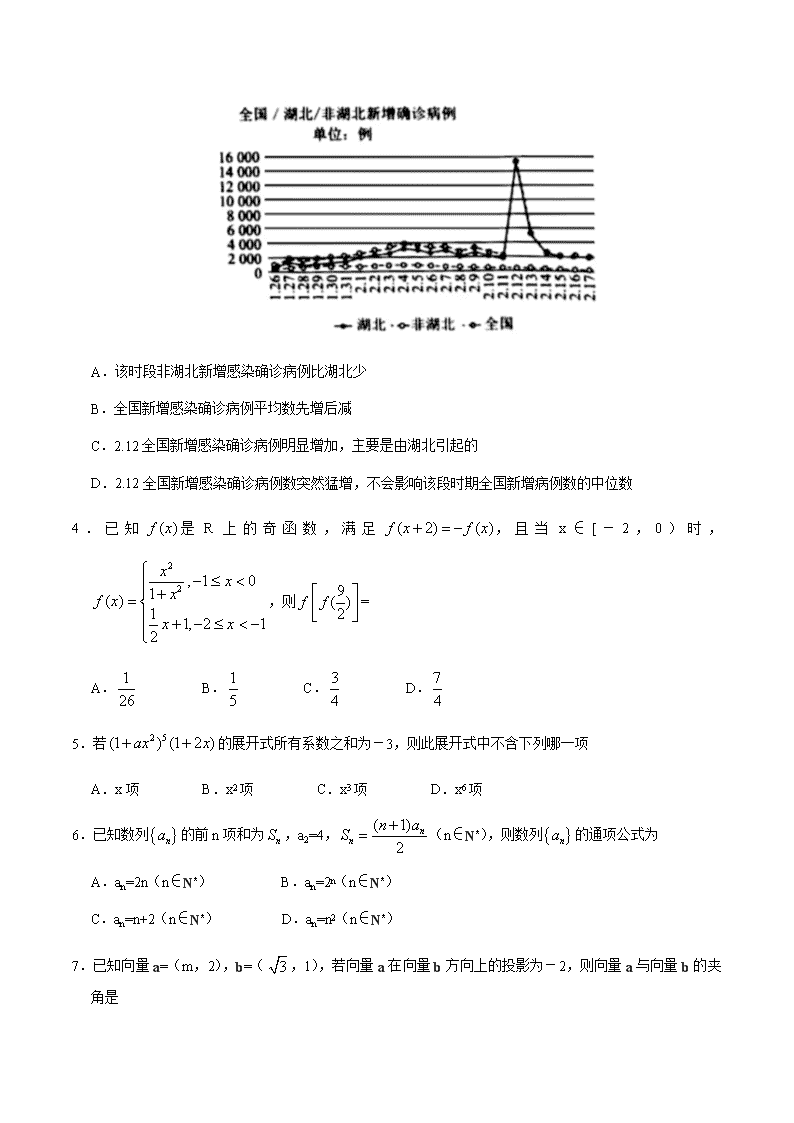
湘赣粤2020届高三6月大联考理科数学试题
姓名 准考证号 (在此卷上答题无效) 绝密★启用前 2020届湘赣粤高三(6月)大联考 理科数学 本试卷共4页。全卷满分150分,考试时间120分钟。 注意事项: 1.答题前,考生务必将自己的姓名、准考证号填写在答题卡上。 2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷上无效。 3.考试结束后,将本试卷和答题卡一并交回。 一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.设集合M={x|x2-x-2>0},集合N={x|),则M∩N= A.{x|x>2} B.{x|x>1} C.(x|x>2或x<-1) D.{x|x>1或x<-1} 2.设i为虚数单位,复数,则= A. B. C.2 D. 3.2019年12月12日我国出现了新型冠状病毒所感染的肺炎,新型冠状病毒的传染性极强.下图是2020年1月26号到2月17号全国/湖北/非湖北新增新型冠状病毒感染确诊病例对比图,根据图象下列判断错误的是 A.该时段非湖北新增感染确诊病例比湖北少 B.全国新增感染确诊病例平均数先增后减 C.2.12全国新增感染确诊病例明显增加,主要是由湖北引起的 D.2.12全国新增感染确诊病例数突然猛增,不会影响该段时期全国新增病例数的中位数 4.已知是R上的奇函数,满足,且当x∈[-2,0)时,,则= A. B. C. D. 5.若的展开式所有系数之和为-3,则此展开式中不含下列哪一项 A.x项 B.x2项 C.x3项 D.x6项 6.已知数列的前n项和为,a2=4,(n∈N*),则数列的通项公式为 A.an=2n(n∈N*) B.an=2n(n∈N*) C.an=n+2(n∈N*) D.an=n2(n∈N*) 7.已知向量a=(m,2),b=(,1),若向量a在向量b方向上的投影为-2,则向量a与向量b的夹角是 A.30° B.60° C.120° D.150° 8.由实数组成的等比数列的前n项和为.则“a1>0”是“S11>S10”的 A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件 9.骰子,古代中国民间娱乐用来投掷的博具,早在战国时期就有.最常见的骰子是正六面体,也有正十四面体、球形十八面体等形制的骰子,如图是满城汉墓出土的铜茕,它是一个球形十八面体骰子,有十六面刻着一至十六数字,另两面刻“骄”和“酒来”,其中“骄”表示最大数十七,“酒来”表示最小数零,每投一次,出现任何一个数字都是等可能的。现投掷铜茕三次观察向上的点数,则这三个数能构成公比不为1的等比数列的概率为 A. B. C. D. 10.已知双曲线(a>0,b>0)的左、右焦点分别为F1、F2,实轴的两个端点分别为A1、A2,虚轴的两个端点分别为B1、B2.以坐标原点O为圆心,|B1B2|为直径的圆O(b>a)与双曲线交于点M(位于第二象限),若过点M作圆的切线恰过左焦点F1,则双曲线的离心率是 A. B.2 C. D. 11.已知函数,x∈R,则下列命题中: ①的最小正周期是,最大值是; ②的单调增区问是(k∈Z); ③; ④将的图象向右平移个单位可得函数的图象, 其中正确个数为 A.1 B.2 C.3 D.4 12.在三棱锥A—BCD中,AB=BC=CD=DA=,BD=,二面角A—BD—C是钝角。若三棱锥A—BCD的体积为2.则三棱锥A—BCD的外接球的表面积是 A.12 B. C.13 D. 二、填空题:本大题共4小题,每小题5分,共21分 13.若点(x,y)在不等式组,所表示的区域内,则目标成数的最大值与最小值之和为 . 14.2018年5月至2019年春,在阿拉伯半岛和伊朗西南部,沙漠蚂虫迅速繁衍,呈现几何式的爆发,仅仅几个月,蝗虫数量增长了8000倍,引发了蝗灾,到2020年春季蝗灾已波及印度和巴基斯坦,假设蝗虫的日增长率为5%,最初有N0只.则经过 天能达到最初的16000倍(参考数据:ln1.05≈0.0488,ln1.5≈0. 4055,ln1600≈7.3778,ln16000≈9.6803). 15.设抛物线y2=2x的焦点为F,过焦点F作直线MN⊥x轴,交抛物线于M,两点,再过F点作直线AB使得AB∥OM其中O是坐标原点),交抛物线于A、B两点,则三角形ABN的面积是 . 16.函数在(0,1)内有两个零点,明实数b的取值范围是 . 三、解答题:共70分,解答题应写出文字说明、证明过程或演算步骤,第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答. (一)必考题:共60分. 17.(12分)已知△ABC的三个内角A,B,C所对的边分别为a,b,c.且=,cosA=,△ABC的面积S=21. (1)求边b和c; (2)求角B. 18.(12分)如图,四棱锥P—ABCD中,∠BAD=60°,AC平分∠BAD.AB⊥BC.AC⊥CD. (1)设E是PD的中点,求证:CE∥平面PAB; (2)设PA⊥平面ABCD,若PD与平面ABCD所成的角为45°,求二面角A—PC—B的余弦值. 19.(12分)已知椭圆的中心在原点,焦点在x轴上,长轴的两个端点分别为A1、A2.短轴的两个端点分别为B1,B2.菱形A1B1A2B2的面积为,离心率. (1)求椭圆的标准方程; (2)设M(-1,0),N(0,-),经过点M作斜率不为0的直线l交椭圆C于A、B两点,若,求直线l的方程. 20.(12分)已知函数(a∈R) (1)当a=-1时,证明函数在区间(-2.2)上有三个极值点; (2)若对于x∈R恒成立,求a的取值范围. 21.(12分)时至21世纪.环境污染已经成为世界各国面临的一大难题,其中大气污染是目前城市急需应对的一项课题。某市号召市民尽量减少开车出行以绿色低碳的出行方式支持节能减排。原来天天开车上班的王先生积极响应政府号召,准备每天从骑自行车和开小车两种出行方式中随机选择一种方式出行.从即日起出行方式选择规则如下:第一天选择骑自行车方式上班,随后每天用“一次性抛掷6枚均匀硬币”的方法确定出行方式,若得到的正面朝上的枚数小于4,则该天出行方式与前一天相同,否则选择另一种出行方式。 (1)求王先生前三天骑自行车上班的天数X的分布列; (2)由条件概率我们可以得到概率论中一个很重要公式——全概率公式.其特殊情况如下:如果事件A1A2相互对立并且P(Ai)>0(i=1,2),则对任一事件B有. 设(n∈N*)表示事件“第n天王先生上班选择的是骑自行车出行方式”的概率. (i)用表示(n≥2); (ii)王先生的这种选择随机选择出行方式有没有积极响应该市政府的号召,请说明理由. (二)选考题:共10分.请考生在22、23题中任选一题作答,如果多做,则按所做的第一题计分. 22.[选修4—4:坐标系与参数方程](10分) 已知圆C的极坐标方程为,直线l的参数方程为(t为参数,a∈R),假设极点与直角坐标原点重合,极轴与直角坐标的非负半轴重合. (1)求圆C的直角坐标的标准方程,并指出圆心和半径; (2)若直线l与圆C相交于A、B两点且|AB|=,求a的值. 23.[选修4—5:不等式选讲](10分) 已知函数. (1)解不等式; (2)当m≥-1时,函数的图象与x轴围成一个三角形,求实数m的取值范围.查看更多