安徽六校教育研究会2020届高三第二次素质测试 文科数学
·1·
安徽六校教育研究会 2020 届高三第二次素质测试
数学(文科)
一、选择题:本大题共 12 小题,每题 5 分.满分 60 分。在每小题给出的四个选项中,只有一个是
符合题目要求的。
1.己知集合 A={x|-2≤x<1 或 2
0,b>0)的右焦点为 F,O 为坐标原点,以 OF 为直径的圆与双曲
线 C 的一条渐近线交于点 O 及点 A ,则双曲线 C 的方程为
A. B. C. D.
8.《易经>包含着很多哲理,在信息学、天文学中都有广泛的应用,《易经》的博大精深, 对今
天的几何学和其它学科仍有深刻的影响,下图就是《易经》中记载的几何图形一一八卦田,图中正
八边形代表八卦,中间的圆代表阴阳太极图,图中八块面积相等的曲边梯形代表八卦田.已知正八
边形的边长为 l0m,代表阴阳太极图的圆的半径为 4m,则每块八卦田的面积约为
A.114 m2 B. 57m2 C.54 m2 D.48 m2
9.锐角△ABC 中,角 A,B,C 所对的边分别为 a,b,c,若
,则角 C 的大小为
A. B. C. D.
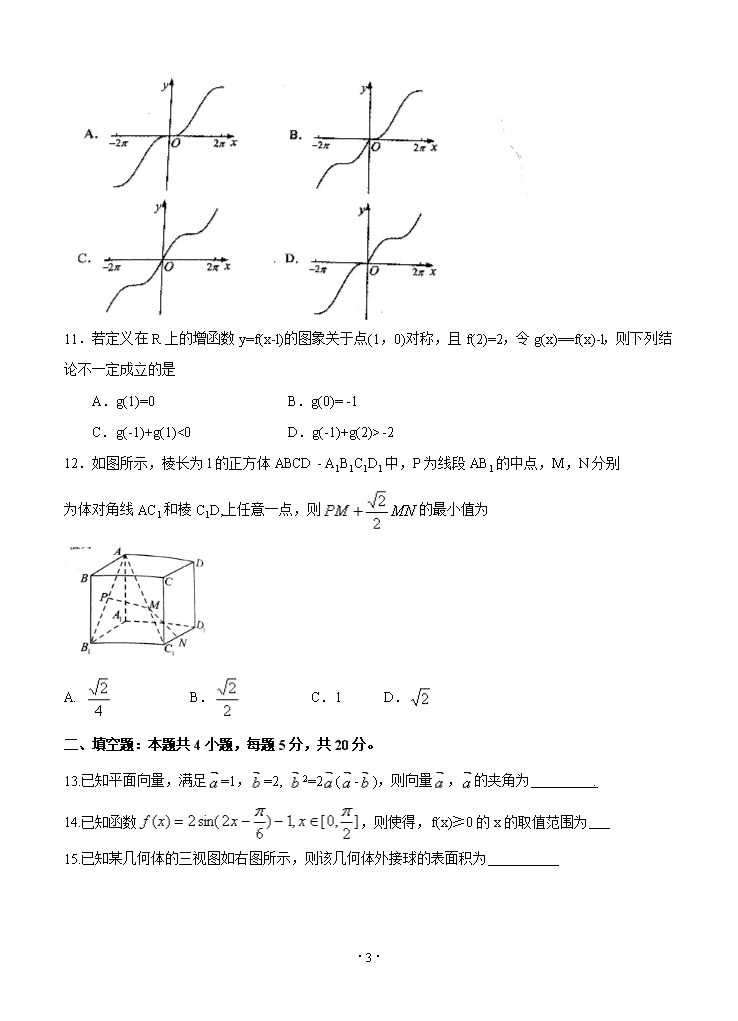
10.函数 y=sin|x|+x 在 x∈[-2 ,2 ]上的大致图象是
·3·
11.若定义在 R 上的增函数 y=f(x-l)的图象关于点(1,0)对称,且 f(2)=2,令 g(x)==f(x)-l,则下列结
论不一定成立的是
A.g(1)=0 B.g(0)= -1
C.g(-1)+g(1)<0 D.g(-1)+g(2)> -2
12.如图所示,棱长为 l 的正方体 ABCD - A1B1C1D1 中,P 为线段 AB1 的中点,M,N 分别
为体对角线 AC1 和棱 C1D,上任意一点,则 的最小值为
A. B. C.1 D.
二、填空题:本题共 4 小题,每题 5 分,共 20 分。
13.已知平面向量,满足 =1, =2, 2=2 ( - ),则向量 , 的夹角为 .
14.已知函数 ,则使得,f(x)≥0 的 x 的取值范围为
15.已知某几何体的三视图如右图所示,则该几何体外接球的表面积为
·4·
16.已知点 P 为直线 ax+y-4=0 上一点,PA,PB 是椭圆 C: (a>1)的两条切线,若恰好
存在一点 P 使得 P⊥PB,则椭圆 C 的离心率为 .
三、解答题:共 70 分。解答应写出文字说明、证明过程或演算步骤。第 17—21 题为必考题,每个
试题考生都必须作答。第 22、23 题为选考题,考生根据要求作答。
(一)必考题:60 分。
17. (12 分)
已知数列{an}的前 n 项和为 Sn,且 2Sn=3an-3n+1+3(n∈N*).
(1)设 bn= ,求证:数列{bn}为等差数列,并求出数列{an}的通项公式;
(2)设 ,Tn=cl+c2+c3+…+cn,求 Tn.
18. (12 分)
受“非洲猪瘟”的影响,10 月份起,某地猪肉的单价随着每周供应量的不足而上涨,具体情形
统计如下表所示:
(1)求猪肉单价 y 关于 x 的线性回归方程 ˆˆ ˆy bx a
(2)当地有关部门已于 11 月初购入进口猪肉,如果猪肉单价超过 30 元/斤,则释放进
·5·
口猪肉增加市场供应量以调控猪肉价格,试判断自受影响后第几周开始需要释放进口猪肉?
参考数据: ,参考公式:
19.(12 分)
如图,四棱锥 P-ABCD 中,侧面 PAB 是等腰直角三角形,PA=PB,BC⊥平面 PAB,AB=BC=2,
AD=BD= .
(1)求证:PA⊥平面 PBC:
(2)求顶点 C 到平面 PAD 的距离.
20.(12 分)
已知函数 f(x)=ex(ex-λcosx) -l,且曲线 y=f(x)在 x=0 处的切线经过点(1,6).
(l)求实数λ的值:
(2)若函数 g(x)= ,试判断函数 g(x)的零点个数并证明.
备注:原卷有错,红色为修正
21. (12 分)
已知抛物线 C:y2=4x 的焦点为 F,点 A(a,3),P 为抛物线 C 上一动点,O 为坐标原点.
(1)若|PA|+|PF|的最小值为 5,求实数 a 的值:
(2)若梯形 OPMN 内接于抛物线 C,OP∥MN,OM,PN 的交点恰为 A,且
|MN|=5 ,求直线 MN 的方程.
(二)选考题:共 10 分。请考生在第 22、23 题中任选一题作答。如果多做,则按所做的第一题计
分。
·6·
22.[选修 4-4:坐标系与参数方程](10 分)
在直角坐标系 xOy 中,曲线 C1 的参数方程为 (t 为参数,α为实数)
以坐标原点 O 为极点,x 轴的正半轴为极轴建立极坐标系,曲线 C2 的极坐标方程为
ρ =8sinθ,曲线 Cl 与曲线 C2 交于 A,B 两点,线段 AB 的中点为 M.
(1)求线段 AB 长的最小值;
(2)求点 M 的轨迹方程.
23.[选修 4-5:不等式选讲](10 分)
已知非零实数 a,b 满足 a
查看更多