数学文卷·2018届陕西省黄陵中学高三（普通班）上学期期末考试（2018

数学文卷·2018届陕西省黄陵中学高三（普通班）上学期期末考试（2018

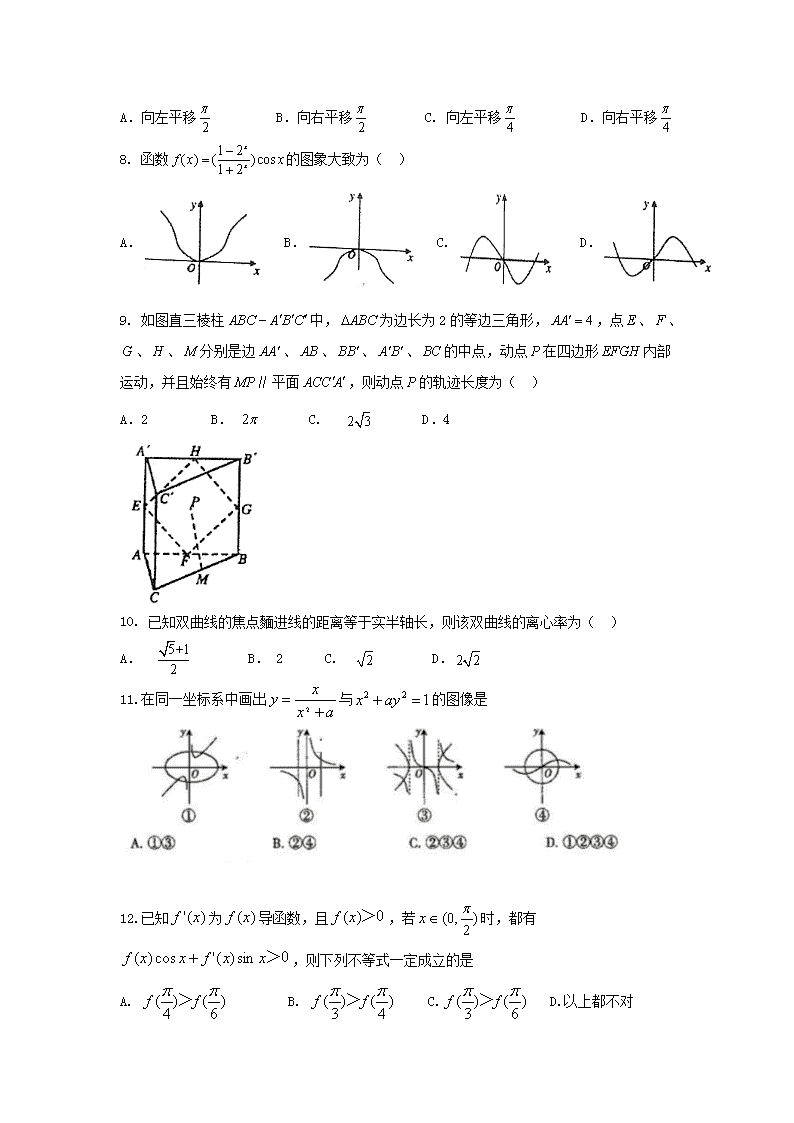
高三普通班期末考试数学试题（文）‎ 第I卷 一、选择题（本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．）‎ ‎1. 若集合,则的子集个数为( )‎ ‎ A．2 B．3 C．4 D．16‎ ‎2. 已知点A（0,1），B（3,2），向量=（-7，-4）,则向量=( )‎ A.（-4，-3） B.（10,5） C.（-1,4） D.（3，4）‎ ‎3. 已知为虚数单位，复数满足，则（ ）‎ A． B． C． D．‎ ‎4. 有5张卡片（除颜色外无差别），颜色分别为红、黄、蓝、绿、紫.从这5张卡片中任取2张不同颜色的卡片，则取出的2张卡片中含有红色卡片的概率为（ ）‎ A. B. C. D.‎ ‎5.已知点在以原点为顶点、以坐标轴为对称轴的抛物线上，抛物线的焦点为，准线为，过点作的垂线，垂足为，若，的面积为，则焦点到准线的距离为( )‎ A. B. C. D.‎ ‎6. 某几何体的三视图如图所示，则其体积为（ ）‎ A． 207 B． C. D． ‎ ‎7. 函数如何平移可以得到函数图象（ ）‎ A．向左平移 B．向右平移 C. 向左平移 D．向右平移 ‎ ‎8. 函数的图象大致为（ ）‎ A． B． C. D．‎ ‎9. 如图直三棱柱中，为边长为2的等边三角形，，点、、、、分别是边、、、、的中点，动点在四边形内部运动，并且始终有平面，则动点的轨迹长度为（ ）‎ A．2 B． C. D．4‎ ‎10. 已知双曲线的焦点麵进线的距离等于实半轴长，则该双曲线的离心率为（ ）‎ A． B． 2 C. D． ‎ ‎11.在同一坐标系中画出与的图像是 ‎12.已知为导函数，且，若时，都有，则下列不等式一定成立的是 A. B. C. D.以上都不对 二、填空题：本大题共4小题，每小题5分，共20分 ‎13．已知向量=（2，6），=（﹣1，λ），若，则 λ =　 　．‎ ‎14．若直线=1（a＞0，b＞0）过点（1，2），则2a+b的最小值为　 　．‎ ‎15. 已知直线与圆心为的圆相交于两点，‎ ‎ 若，则实数= ‎ ‎16. 已知函数是定义在上的奇函数，当时，，给出下列命题：‎ ‎ ① 当时，；‎ ‎ ② 函数的单调递减区间是；‎ ‎ ③ 对，都有.‎ ‎ 其中正确的命题是 （只填序号） ‎ 三、解答题：本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．‎ ‎17．（10分）‎ ‎ 在中，角所对边分别是，满足 ‎ （1）求的值；（2）若，求和的值. ‎ ‎18．（12分） ‎ ‎ 已知是等比数列，，是等差数列，，‎ ‎ （1）求和的通项公式；‎ ‎ （2）设，求数列的前项和.‎ ‎19.（本题满分12分）‎ 在中，三个内角，，所对的边分别记为，，，并且.‎ ‎（Ⅰ）若，求 ‎（Ⅱ）若，且的面积，求和的值.‎ ‎20..（本题满分12分）‎ 如图，几何体中，平面，是正方形，为直角梯形，,,是腰长为的等腰直角三角形.‎ ‎（Ⅰ）求证：；‎ ‎（Ⅱ）求几何体的体积.‎ ‎【来源：全,品…中&高*考+网】‎ ‎21.(本题满分12分)已知函数.‎ ‎(1)讨论f(x)的单调性; (2)设,若存在, ,且,使不等式成立,求实数k的取值范围.‎ ‎22.（本小题满分12分）‎ 在直角坐标系中，曲线（为参数且），其中，在以为极点，轴正半轴为极轴的极坐标系中，曲线．‎ ‎（Ⅰ）求与交点的直角坐标；‎ ‎（Ⅱ）若与相交于点，与相交于点，求当时的值．‎ ‎1--5 CAACD ‎ ‎6-10: BDCDC 11.C 12.D ‎13．﹣3　．　 14．8. ‎ ‎15. ; 16. ②③‎ 三、解答题 ‎17． ‎ 解（1）由题意得， ------------------2分 ‎ 所以 ‎ 因为 ‎ 所以 -----------------------------------------------------------------------------5分 ‎ (2）由得 ----------------------7分 ‎ 由可得 ------------------9分 ‎ 所以代入可得 ------------------10分 ‎18． ‎ 解（1）设的公比为，由得，所以 ------3分 ‎ 设的公差为，由得，所以 ------6分 ‎（2）的前n项和为： -----------------------9分 ‎ 的前n项和为： -------11分 ‎ 所以的前项和= -----------------------------12分 ‎19. (Ⅰ) ‎ ‎(Ⅱ)‎ ‎ ‎ 又 或 ‎20. (Ⅰ)易证面 (Ⅱ)‎ ‎21..解:(1)∵f′(x)=x+(2a-2)- = = (x＞0).令f′(x)=0得x=2或x=-2a.‎ ‎ ∴①当-2a=2,即a=-1时, f′(x)≥0在x＞0时恒成立,即f(x)在(0,+∞)上单调递增.……(2分)‎ ‎②当-2a＞2,即a＜-1时,f(x)在(0,2)和(-2a,+∞)上单调递增,在(2,-2a)上单调递减.………(3分)‎ ‎③当0＜-2a＜2,即-1＜a＜0时,f(x)在(0,-2a)和(2,+∞)上单调递增,在(-2a,2)上单调递减.…(4分)‎ ‎ ④当-2a≤0,即a≥0时,f(x)在(0,2)上单调递减,在(2,+∞)上单调递增. ………(5分)‎ ‎(2)由(1)知,当a=1时,f(x)在(2,+∞)上单调递增,不妨设x2＞x1＞2,‎ 则不等式|f(x1)-f(x2)|≤k|lnx1-lnx2|可化为f(x2)-f(x1)≤klnx2-klnx1.…………(7分)‎ f(x1)-klnx1≥f(x2)-klnx2,令g(x)= f(x)-klnx,则g(x)在(2,+∞)上存在单调递减区间. ……(9分)‎ ‎∴g′(x)= f′(x) - ＜0 在区间(2,+∞)有解,即- ＜0在x∈(2,+∞)上有解,…(10分)‎ ‎∴k＞x2-4, x∈(2,+∞),故k＞0. ……………(12分)‎ ‎22.解析：（Ⅰ）由题设有曲线的直角坐标方程为，‎ 曲线的直角坐标方程为，联立解得或， 即与交点的直角坐标为和 ‎（Ⅱ）曲线的极坐标方程为其中 因此的极坐标为，的极坐标为。‎ 所以，当时，.‎