数学理卷·2018届河北省沧州市第一中学高二12月学情检测（2016-12）word版

数学理卷·2018届河北省沧州市第一中学高二12月学情检测（2016-12）word版

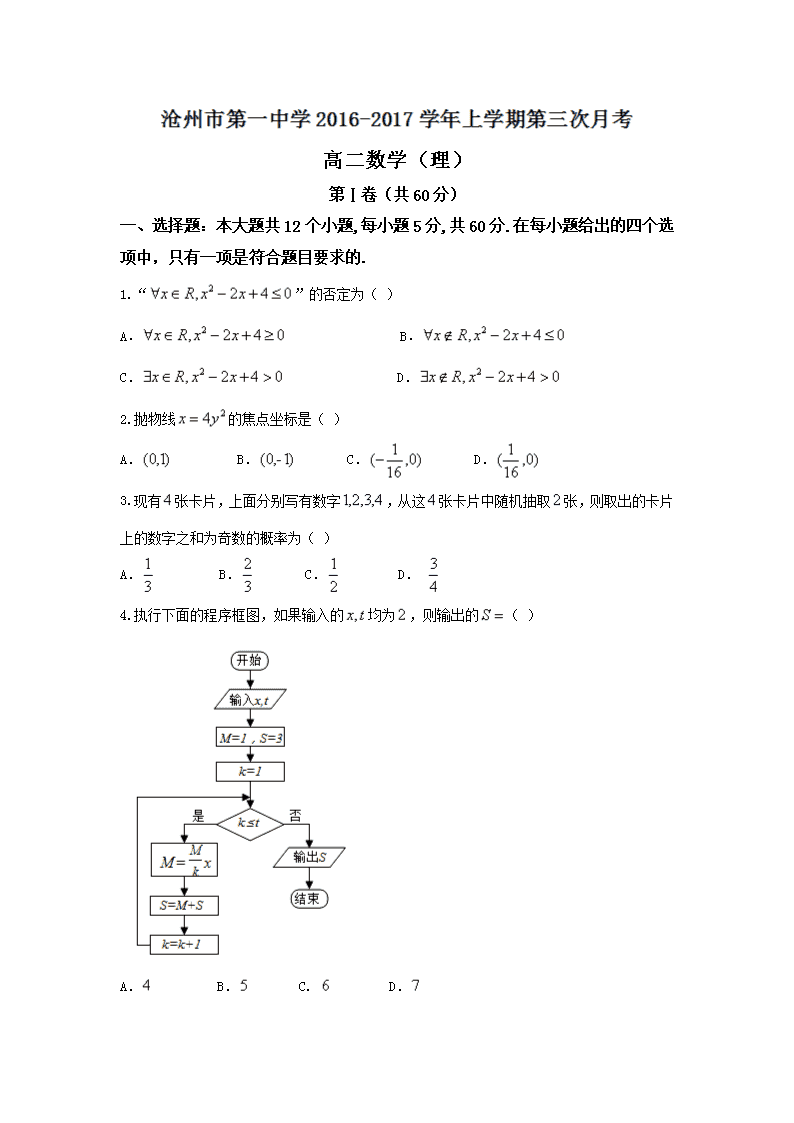
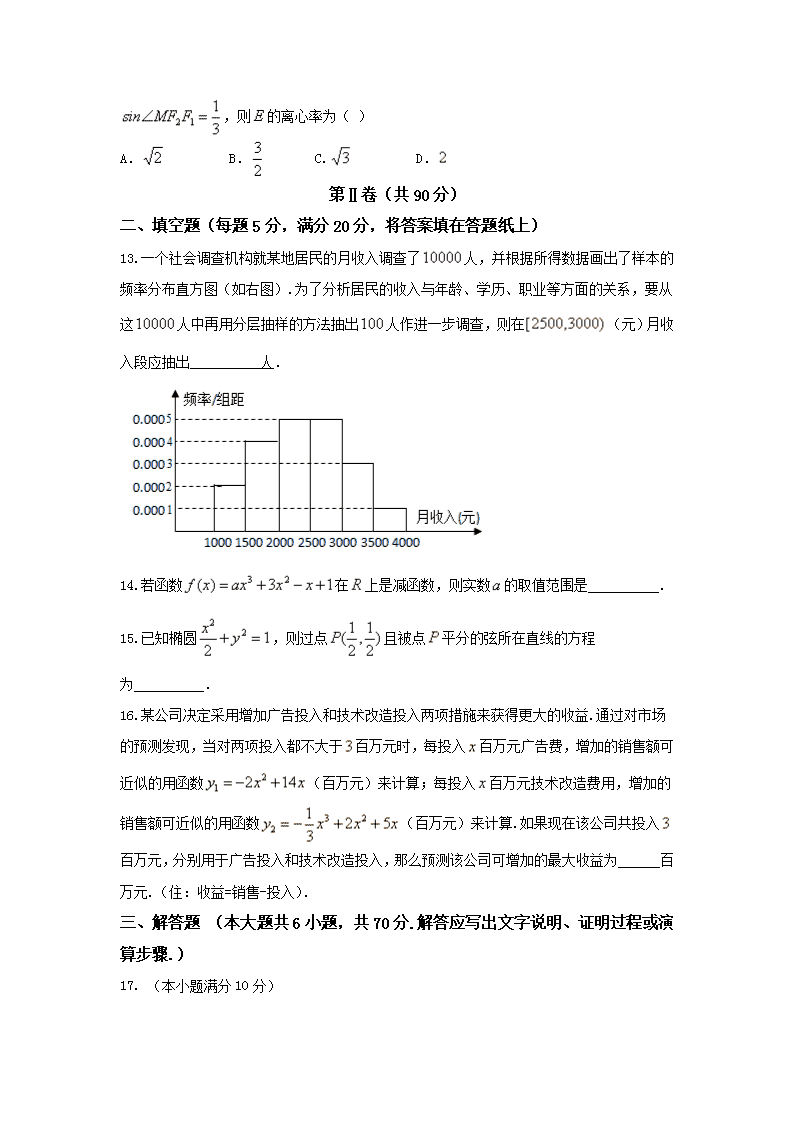
‎ ‎ 高二数学（理）‎ 第Ⅰ卷（共60分）‎ 一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1.“”的否定为（ ）‎ A． B． ‎ C． D．‎ ‎2.抛物线的焦点坐标是（ ）‎ A． B． C． D．‎ ‎3.现有张卡片，上面分别写有数字，从这张卡片中随机抽取张，则取出的卡片上的数字之和为奇数的概率为（ ）‎ A． B． C． D． ‎ ‎4.执行下面的程序框图，如果输入的均为，则输出的（ ）‎ A． B． C. D．‎ ‎5.下列条件中使点与点一定共面的是（ ）‎ A． B． ‎ C. D．‎ ‎6.直三棱柱中，，分别是的中点，，则与所成角的余弦值为（ ）‎ A． B． C. D．‎ ‎7.已知是双曲线的左右焦点，为双曲线上的一点，，则到轴距离为（ ）‎ A． B． C. D．‎ ‎8.长方形中，为的中点，在长方形内随机取一点，取到的点到的距离大于的概率为（ ）‎ A． B． C. D．‎ ‎9.曲线在点处的切线方程为，则（ ）‎ A． B． C. D．‎ ‎10.在棱长为的正方体中，点分别是棱的中点，则点到平面的距离是（ ）‎ A． B． C. D．‎ ‎11.点是抛物线上一动点，则点到点的距离与到直线的距离之和的最小值是（ ）‎ A． B． C. D．‎ ‎12.已知是双曲线的左右焦点，点在上，与轴垂直，‎ ‎，则的离心率为（ ）‎ A． B． C. D．‎ 第Ⅱ卷（共90分）‎ 二、填空题（每题5分，满分20分，将答案填在答题纸上）‎ ‎13.一个社会调查机构就某地居民的月收入调查了人，并根据所得数据画出了样本的频率分布直方图（如右图）.为了分析居民的收入与年龄、学历、职业等方面的关系，要从这人中再用分层抽样的方法抽出人作进一步调查，则在（元）月收入段应抽出 人．‎ ‎14.若函数在上是减函数，则实数的取值范围是 ．‎ ‎15.已知椭圆，则过点且被点平分的弦所在直线的方程为 ．‎ ‎16.某公司决定采用增加广告投入和技术改造投入两项措施来获得更大的收益.通过对市场的预测发现，当对两项投入都不大于百万元时，每投入百万元广告费，增加的销售额可近似的用函数（百万元）来计算；每投入百万元技术改造费用，增加的销售额可近似的用函数（百万元）来计算.如果现在该公司共投入百万元，分别用于广告投入和技术改造投入，那么预测该公司可增加的最大收益为______百万元.（住：收益=销售-投入）．‎ 三、解答题 （本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.） ‎ ‎17. （本小题满分10分）‎ 已知，且是的必要不充分条件，求实数的取值范围.‎ 18. ‎（本小题满分12分）‎ 已知函数在处取得极值为，求的值.‎ 19. ‎（本小题满分12分）‎ 某地区年至年农村居民家庭人均纯收入（单位：万元）的收据如下表：‎ 年份 年份代号 人均纯收入 （1） 求关于的线性回归方程；‎ （2） 利用（1）中的回归方程，分析年至年该地区农村居民家庭人均纯收入的变化情况，并预测该地区年农村居民家庭人均纯收入.‎ 附：回归直线的斜率和截距的最小二乘法估计公式分别为：‎ 20. ‎（本小题满分12分）‎ 如图，在三棱锥中，平面，，分别是的中点，，与交于点，与交于点，连接.‎ （1） 求证：；‎ ‎（2）求二面角的余弦值.‎ ‎21. （本小题满分12分）‎ 已知函数.‎ （1） 当时，求函数的单调区间；‎ ‎（2）若对定义域内的任意恒成立，求的取值范围.‎ ‎22. （本小题满分12分）‎ 如图，椭圆经过点，离心率，直线的方程为.‎ （1） 求椭圆的方程；‎ ‎（2）是经过右焦点的任一弦（不经过点），设直线与直线相交于点，记的斜率分别为.问：是否存在常数，使得？若存在，求的值；若不存在，请说明理由.‎ 沧州一中2016-2017高二上第三次月考（理）答案 一、选择题 ‎1-5:CDBDC 6-10:ABBDA 11、12：CA 二、填空题 ‎13. 14. 15. 16.‎ 三、解答题 ‎17.解：，‎ ‎∵是的必要不充分条件，∴.‎ ‎18.‎ ‎19.（1）‎ ‎（2）∵，∴年至年该地区人均纯收入稳步增长.预计到年，该区人均纯收入（万元），‎ 所以，预计到年，该区人均纯收入约万元左右.‎ 20. ‎（1）证明：因为分别是的中点，‎ （2） 在中，，所以，即，‎ 因为平面，所以，‎ 又，所以平面，由（1）知，‎ 所以平面，又平面，所以，同理可得，‎ 所以为二面角的平面角，设，‎ 在中，由勾股定理得，，‎ 在中，由勾股定理得，，‎ 又为的重心，所以，同理，‎ 在中，由余弦定理得，‎ 即二面角的余弦值为.‎ 21. 解：.‎ （1） ‎①当时，的变化情况如下表：‎ ‎+‎ ‎-‎ ‎+‎ 单调递增 极大值 单调递减 极小值 单调递增 所以函数的单调递增区间是，，单调递减区间是.‎ ‎②当时，的变化情况如下表：‎ ‎+‎ ‎-‎ ‎+‎ 单调递增 极大值 单调递减 极小值 单调递增 所以函数的单调递增区间是，，单调递减区间是.‎ ‎③当时，，此时单调递增.‎ 所以函数的单调递增区间是，没有单调递减区间.‎ ‎（2）由于，显然时，，此时对定义域内的任意不是恒成立的，当时，易得函数在区间的极小值，也是最小值即是，此时只要即可，解得，所以实数的取值范围是.‎ ‎22.解：（1）由在椭圆上得，，①‎ 依题意知，则，②‎ ‎②代入①解得，故椭圆的方程为.‎ （1） 设，则直线的方程为：，‎ 令，求得，从而直线的斜率为，‎ 联立，得，‎ 则直线的斜率为：，直线的斜率为：，‎ 所以，‎ 故存在常数符合题意.‎