- 2021-06-19 发布 |
- 37.5 KB |
- 7页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
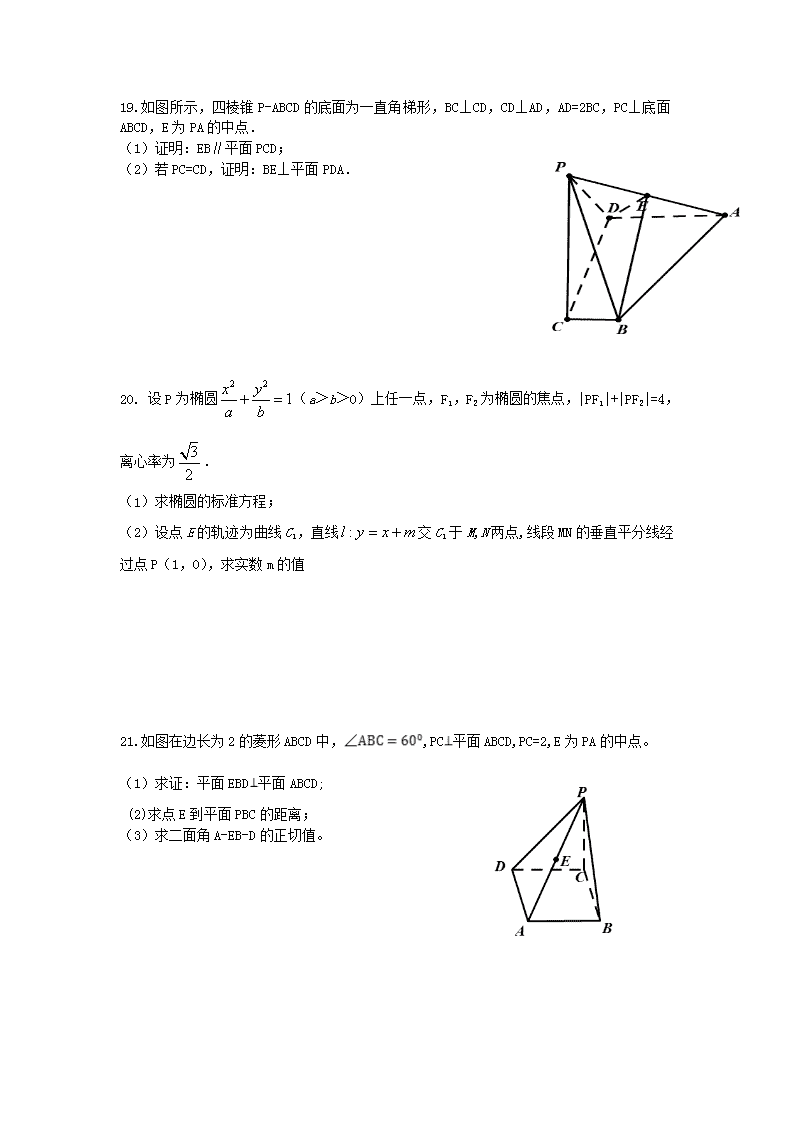
数学理卷·2018届安徽省池州市东至二中高二上学期12月份阶段考试(2016-12)
东至二中2016—2017学年第一学期高二年级阶段测试(2) 数 学(理)试 卷 考试时间:120分钟 命题人:周木新 一、选择题(本大题共12小题,共60分) 1.一个梯形采用斜二测画法作出其直观图,则其直观图的面积是原来梯形面积的( ) A.倍 B. 倍 C. 倍 D倍 2. 空间中,可以确定一个平面的条件是( ) A.三个点 B.四个点 C.三角形 D.四边形 3. 直线的倾斜角是( ) A.30° B. 120° C. 60° D.150° 4.若点P为两条异面直线l,m外的任意一点,则( ) A.过点P有且仅有一条直线与l,m都平行 B. 过点P有且仅有一条直线与l,m都异面 C.过点P有且仅有一条直线与l,m都相交 D. 过点P有且仅有一条直线与l,m都垂直 5.若直线l不平行于平面a,且la,则( ) A.a内所有直线与l异面 B. a内的直线与l都相交 C.a内存在唯一的直线与l平行 D. a内不存在与l平行的直线 6. 已知α,β是两个不同的平面,则“平面α∥平面β”成立的一个充分条件是( ) A.存在一条直线l,l⊂α,l∥β B.存在一个平面γ,γ⊥α,γ⊥β C.存在一条直线l,l⊥α,l⊥β D.存在一个平面γ,γ∥α,γ⊥β 7. 已知椭圆,直线,那么直线与椭圆位置关系() A相交 B相离 C相切 D不确定 8.已知点P(2,-3)、Q(3,2),直线与线段PQ相交,则的取值范围是( ) A. B. C. D. 9. 某几何体的三视图如图,其正视图中的曲线部分为半个圆弧,则该几何体的表面积为 10.已知直线ax+by+c=0(a,b,c都是正数)与圆 相切,则以a,b,c为三边长的三角形( ) A.锐角三角形 B. 直角三角形 C. 钝角三角形 D.不存在 11.设P,Q分别为直线x-y=0和圆上的点,则|PQ|的最小值为( ) A.4 B. C. D. 12.过点P(3,2)作曲线C:的两条切线,切点分别为A,B,则直线AB的方程为( ) A.2x-2y-3=0 B.2x+2y-3=0 C. x-y+1=0 Dx+y+1=0 二、填空题(本大题共4小题,共20分) 13. 点P(1,-1)到直线3x-4y+3=0的距离是 ______ . 14. 在空间直角坐标系中,点(1,2,3)关于平面xoy对称的点坐标是 ______ . 15. 已知M,N分别为椭圆C的左右焦点,P为椭圆C上的点,若椭圆C存在4个点满足条件,那么椭圆的离心率取值范围______ . 16. 已知椭圆,点F为椭圆的左焦点,点P为椭圆上任意一点,点A(5,4),那么的最小值______ . 三、解答题(本大题共6小题,共70分,其中17题10分,其余每题12分) 17.已知直线l1:2x-y-3=0,l2:x-my+1-3m=0,m∈R. (1)若l1∥l2,求实数m的值; (2)若l2在两坐标轴上截距相等,求直线l2的方程. 18. 已知p:实数x满足,其中a<0;q:实数x满足,且p是q的充分条件,求的取值范围. 19.如图所示,四棱锥P-ABCD的底面为一直角梯形,BC⊥CD,CD⊥AD,AD=2BC,PC⊥底面ABCD,E为PA的中点. (1)证明:EB∥平面PCD; (2)若PC=CD,证明:BE⊥平面PDA. 20. 设P为椭圆(a>b>0)上任一点,F1,F2为椭圆的焦点,|PF1|+|PF2|=4,离心率为. (1)求椭圆的标准方程; (2)设点E的轨迹为曲线C1,直线交C1于M,N两点,线段MN的垂直平分线经过点P(1,0),求实数m的值 21.如图在边长为2的菱形ABCD中,,PC平面ABCD,PC=2,E为PA的中点。 (1)求证:平面EBD平面ABCD; (2)求点E到平面PBC的距离; (3)求二面角A-EB-D的正切值。 22. 设圆的圆心为A,直线过点B(,0)且与x轴不重合,交圆A于C,D两点,过B作AC的平行线交AD于点E. (1)证明为定值,并写出点E的轨迹方程; (2)过点做直线MA,MB分别与椭圆相交与A,B两点,满足直线MA与MB的倾斜角互补,判断直线AB的斜率是否为定值,若为定值求出此定值,若不为定值说明理由。 东至二中2016-2017学年第一学期高二年级阶段测试(2) 数学(理)试卷答案 选择题1A 2C 3B 4D 5D 6C 7A 8C 9C 10D 11D 12B 填空题13. 2 14.(1,2,-3) 15. (0.5,1) 16. 5-2 解答题17(1)m=0.5 (2)m=或m=-1 18. 19. (1)证明取PD中点F,连结EF,CF 因为E为PA中点,F为PD中点 所以EF∥AD 且AD=2EF, 又因为BC⊥CD,AD⊥CD 所以CB∥AD, 又由AD=2CB 所以EF∥CB,CB=EF 所以四边形CBEF为平行四边形 所以 又因为CF平面PCD,BE平面PCD 所以BE∥平面PCD (2) F为PD中点, PC=CD 所以CF⊥PD PC⊥底面CBAD 所以PC⊥AD, 又AD⊥CD,PCCD=C 所以AD⊥平面PCD 又CF平面PCD 所以AD⊥CF 又PDAD=D 所以CF⊥平面PAD 由(1)知BE∥CF 所以BE⊥平面PAD 20(1)方程为 (2) 联立直线方程与椭圆方程消去y得 设M(),N(),线段MN的中点为Q() 则=,由得 又因为线段MN的垂直平分线经过点P(1,0) 所以线段MN的垂直平分线方程y=-x+1 解得 由=, 解得 m= 21(1)证明:连结BD,AC相交于点 O,连结EO 因为四边形ABCD为平行四边形 所以O为AC的中点 ,又因为E为PA的中点, 所以OE∥PC,由PC平面ABCD,所以OE平面ABCD 又因为OE平面EBD,所以平面EBD平面ABCD; (2) , PC=2 PC平面ABCD 所以A点到平面PBC的距离为 因为E为PA的中点 所以E点到平面PBC的距离为 (3)过点O作OF垂直BE于F点,连结OF,AF 由AOBD,AOOE,BDOE=O,所以AO平面BDE, AOBE, OFBE, AOOF=O,所以平面AOF 所以二面角A-EB-D的平面角为 在直角AFO中tan= 22(1)证明因为BE∥AC 所以 所以 又因为AD=AC=4 所以DE=BE 又因为AE+DE=4 所以EA+EA=4为定值 由椭圆定义知点E的轨迹方程 (y0) (2) 设A(),B(),直线MA方程y=k(x-1)+,则直线MB方程y=-k(x-1)+ 消去y得, , 用-k代替k得 -= k(-1)+ k(-1) 则直线AB的斜率==查看更多