数学（B）卷·2019届内蒙古巴彦淖尔市第一中学高二上学期期中考试（2017-11）

数学（B）卷·2019届内蒙古巴彦淖尔市第一中学高二上学期期中考试（2017-11）

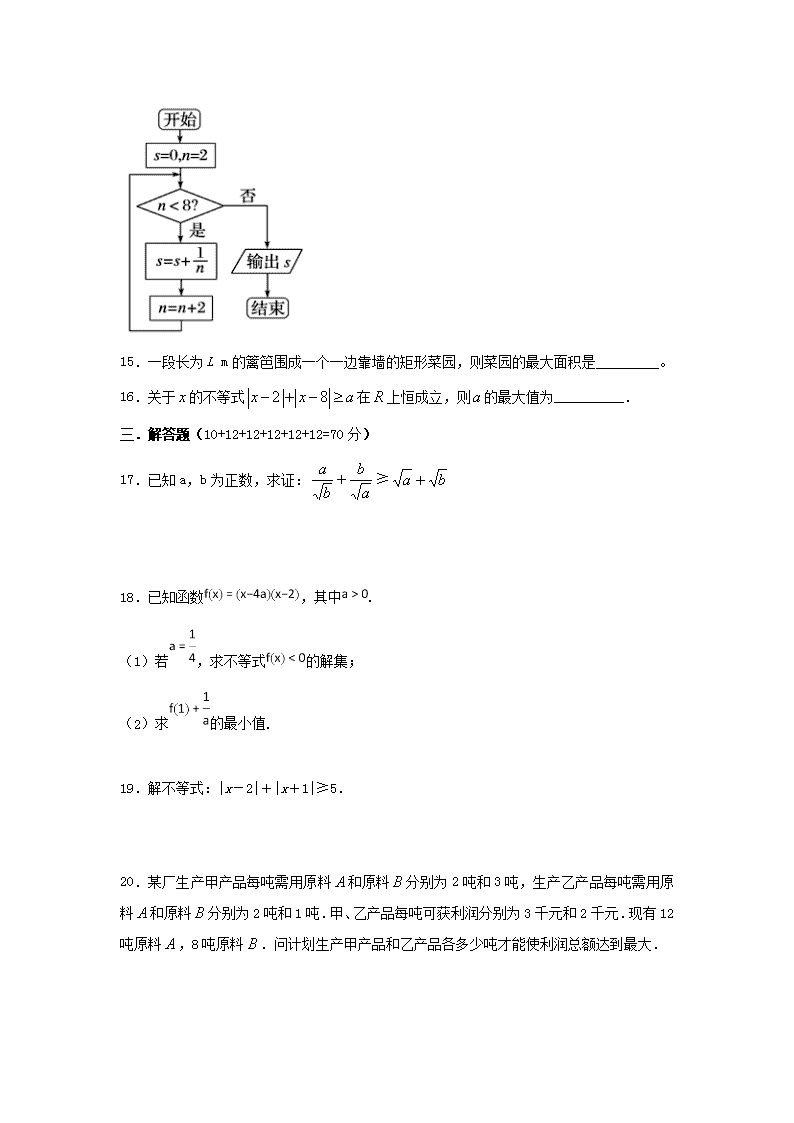
巴彦淖尔市第一中学2017-2018学年第一学期 ‎11月期中考试高二数学试题B卷 命题人:李瑛 一．选择题（5分×12=60分）在每小题给出的四个选项只有一项正确.‎ ‎1．已知且，则下列不等关系正确的是（ ）‎ A. B. C. D. ‎ ‎2．集合A={x|x2+2x＞0}，B={x|x2+2x﹣3＜0}，则A∩B=（　　）‎ A. （﹣3，1） B. （﹣3，﹣2） ‎ ‎ C. R D. （﹣3，﹣2）∪（0，1）‎ ‎3．设，则的最小值为（ ）‎ A. 4 B. ‎5 C. 6 D. 7‎ ‎4．在不等式表示的平面区域内的点是（ ）‎ A. B. C. D. ‎ ‎5若不等式的解集为，则的值为 ( 　 　)‎ A. B. C. D. ‎ ‎6 k进制数3651(k)，则k可能是( )‎ A. 2 B. ‎4 C. 6 D. 8‎ ‎7．不等式的解集是（ ）‎ A. . B. ‎ C. D. ‎ ‎8 函数的最小值为（ ）‎ A. 3 B. ‎4 C. 5 D. 6‎ ‎9．若x,y满足，则z=2x+y的最小值是（ ）‎ A. B. ‎8 C. D. 5‎ ‎10．函数的最小值为（ ）‎ A. B. C. D. ‎ ‎11下边程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”，执行该程序框图，若输入的a，b分别为14，18，则输出的a等于 (　　)‎ A. 0 B. ‎2 ‎ C. 4 D. 14‎ ‎12．已知则的最小值是（ ）．‎ ‎ A B C 2 D 1‎ 二．填空题（5分×4=20分）‎ ‎13．已知点和点在直线的两侧，则的取值范围是　　　　.‎ ‎14．如图所示，程序框图的输出结果是__________‎ ‎15．一段长为L m的篱笆围成一个一边靠墙的矩形菜园，则菜园的最大面积是 。‎ ‎16．关于的不等式在上恒成立，则的最大值为__________．‎ 三． 解答题（10+12+12+12+12+12=70分）‎ ‎17．已知a，b为正数，求证：≥‎ ‎18．已知函数，其中.‎ ‎（1）若，求不等式的解集；‎ ‎（2）求的最小值.‎ ‎19．解不等式：|x－2|＋|x＋1|≥5．‎ ‎20．某厂生产甲产品每吨需用原料和原料分别为2吨和3吨，生产乙产品每吨需用原料和原料分别为2吨和1吨．甲、乙产品每吨可获利润分别为3千元和2千元．现有12吨原料，8吨原料．问计划生产甲产品和乙产品各多少吨才能使利润总额达到最大．‎ ‎21．某工厂修建一个长方体无盖蓄水池，其容积为6400立方米，深度为‎4米．池底每平方米的造价为120元，池壁每平方米的造价为100元．设池底长方形的长为x米．‎ ‎（Ⅰ）求底面积，并用含x的表达式表示池壁面积；‎ ‎（Ⅱ）怎样设计水池能使总造价最低?最低造价是多少?‎ ‎22．已知函数.‎ ‎（Ⅰ）若，解不等式；‎ ‎（Ⅱ）若恒成立，求实数的取值范围.‎ 数学B卷参考答案 一选择题 ‎1D 2D ‎3C 4B 5 B 6D 7B ‎8A 9D ‎10A 11B ‎‎12A 二 填空题 ‎13. 14. 15. 16. 6‎ 三解答题 ‎17：证明 ∵ a>0，b>0，‎ ‎∴ ≥， ≥，‎ 两式相加，得 ‎≥，∴ ≥．‎ ‎18：（1）当时，.不等式的解集为.‎ ‎（2），‎ ‎.，，‎ 当且仅当即时取等号，故的最小值为3.‎ ‎19 解：(1)当x＜－1时，不等式可化为－x＋2－x－1≥5，解得x≤－2； ‎ ‎(2)当－1≤x≤2时，不等式可化为－x＋2＋x＋1≥5，此时不等式无解； ‎ ‎(3)当x＞2时，不等式可化为x－2＋x＋1≥5，解得x≥3； ‎ 所以原不等式的解集为(－∞，－2]∪[3，＋∞).‎ ‎20 解：设计划生产甲产品和乙产品分别为吨，则满足的约束条件为 ‎，总利润．约束条件如图所示，恰好在点处取得最大值，即计划生产甲产品和乙产品分别为1吨和5吨能使得总利润最大．‎ ‎21（Ⅰ）设水池的底面积为S1，池壁面积为S2，‎ 则有 (平方米)．池底长方形宽为米，则 S2＝8x＋8×＝8 (x＋)． ‎ ‎（Ⅱ）设总造价为y，则 y＝120×1 600＋100×8≥192000＋64000＝256000．当且仅当x＝，即x＝40时取等号． ‎ 所以x＝40时，总造价最低为256000元．‎ 答：当池底设计为边长‎40米的正方形时，总造价最低，其值为256000元．‎ ‎22 （Ⅰ）当时，，‎ 即. 解得.‎ ‎（Ⅱ） ，‎ 若恒成立，只需，‎ 即或，‎ 解得或.‎