2018-2019学年湖北省浠水县实验高级中学高二12月月考数学（理）试题 Word版

2018-2019学年湖北省浠水县实验高级中学高二12月月考数学（理）试题 Word版

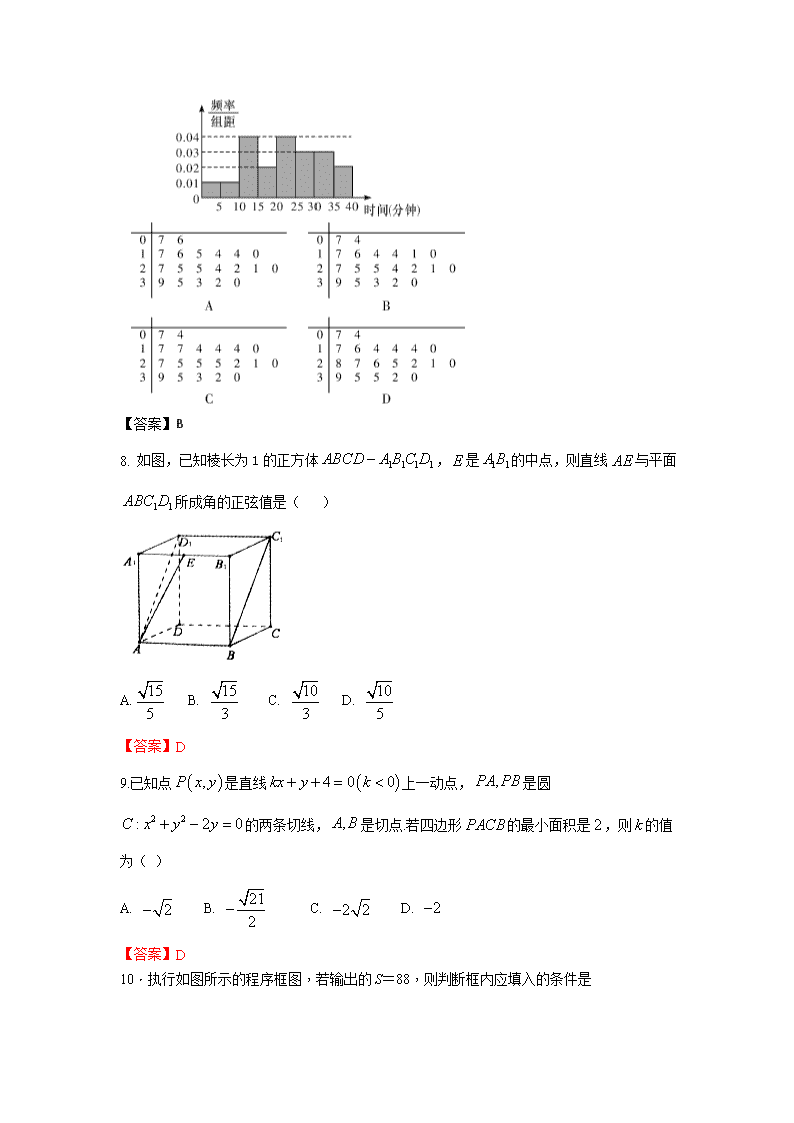
‎2018-2019学年湖北省浠水县实验高级中学高二12月月考理科数学试题 考试时间：120分钟 总分分值：150分 一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1. 设命题则为（ ）‎ A. B. ‎ C. D. ‎ ‎【答案】C ‎2. 抛物线的焦点到双曲线的渐近线的距离为（ ）‎ A. B. C. 1 D. ‎ ‎【答案】B ‎3. 有关下列命题，其中说法正确的个数是（ ）‎ ‎① 命题“若，则”的逆否命题是“若，则”‎ ‎②“”是“”的必要不充分条件 ‎③若是假命题，则都是假命题 ‎④命题“若，则方程有实根”的逆命题为假命题 A. 1 B. ‎2 C. 3 D.4‎ ‎【答案】C ‎4. 在空间直角坐标系，确定的平面记为，不经过点的平面的一个法向量为，则（ ）‎ A. B. C. 相交但不垂直 D. 所成的锐二面角为 ‎【答案】A ‎5．某初级中学有学生270人，其中七年级108人，八、九年级各81人，现要利用抽样方法抽取10‎ 人参加某项调查，考虑选用简单随机抽样、分层抽样和系统抽样三种方案，使用简单随机抽样和分层抽样时，将学生按七、八、九年级依次统一编号为1，2，…，270；使用系统抽样时，将学生统一随机编号1，2，…，270，并将整个编号依次分为10段.如果抽得号码有下列四种情况：‎ ‎ ①7，34，61，88，115，142，169，196，223，250；‎ ‎ ②5，9，100，107，111，121，180，195，200，265；‎ ‎ ③11，38，65，92，119，146，173，200，227，254；‎ ‎ ④30，57，84，111，138，165，192，219，246，270；‎ ‎ 关于上述样本的下列结论中，正确的是（ ）‎ A． ②、③都不能为系统抽样 B． ②、④都不能为分层抽样 C． ①、④都可能为系统抽样 D． ①、③都可能为分层抽样 ‎【答案】D ‎6. 我国古代数学著作《九章算术》中有如下问题：“今有器中米，不知其数，前人取半，中人三分取一，后人四分取一，余米五升．问米几何？”如图是解决该问题的程序框图，执行该程序框图，若输出的S＝5 (单位：升)，则输入k的值为（ ） 7. 5 15 20 25‎ ‎ 第6题图 ‎ ‎【答案】C ‎7．为了了解高一年级学生的体锻情况，学校随机抽查了该年级20个同学，调查他们平均每天在课外从事体育锻炼的时间(分钟)，根据所得数据的茎叶图，以5为组距将数据分为八组，分别是[0，5)，[5，10)，…[35，40]，作出的频率分布直方图如图所示，则原始的茎叶图可能是 ‎【答案】B ‎8. 如图，已知棱长为1的正方体，是的中点，则直线与平面所成角的正弦值是（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎9.已知点是直线上一动点，是圆的两条切线，是切点.若四边形的最小面积是，则的值为（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎10．执行如图所示的程序框图，若输出的S＝88，则判断框内应填入的条件是 A．k＞7 B．k＞‎6 C．k＞5 D．k＞4‎ ‎【答案】C ‎11．若样本的平均数是10，方差为1，则对于样本 ‎，下列结论正确的是（ ）‎ A．平均数为21，方差为2 B．平均数为21，方差为3‎ C．平均数为21，方差为4 D．平均数为21，方差为5‎ ‎【答案】C ‎12.若点分别是椭圆的左顶点和左焦点，过点的直线交曲线于两点，记直线的斜率为，其满足，则直线的斜率为 A.2 B. C. D.‎ ‎【答案】B 二、填空题：本题共4小题，每小题5分，共20分。‎ ‎13．二进制数化为十进制数是　109　．‎ ‎14．用秦九韶算法求当时的值时， _____14___．‎ ‎15．数学与文学之间存在着许多奇妙的联系．诗中有回文诗，如：“云边月影沙边雁，水外天光山外树”，倒过来读，便是“树外山光天外水，雁边沙影月边云”，其意境和韵味读来是一种享受！数学中也有回文数，如：88，454，7337，43534等都是回文数，无论从左往右读，还是从右往左读，都是同一个数，称这样的数为“回文数”，读起来还真有趣！‎ 二位的回文数有11，22，33，44，55，66，77，88，99，共9个；‎ 三位的回文数有101，111，121，131，…，969，979，989，999，共90个；‎ 那么，5位的回文数总共有　900　个．‎ ‎16.设F1，F2分别是椭圆的左、右焦点，直线过F1交椭圆C于A，B两点，交y轴于C点，若满足且，则椭圆的离心率为______‎ 三．解答题（本大题共6小题，共70分.应写出文字说明、证明过程或推演步骤）‎ ‎17.(本小题满分10分）下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量 (吨）与相应的生产能耗 (吨标准煤）的几组对照数据：‎ x ‎2‎ ‎4‎ ‎6‎ ‎8‎ y ‎4‎ ‎5‎ ‎7‎ ‎8‎ ‎（1）请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程；‎ ‎（2）已知该厂技改前生产100吨甲产品的生产能耗为90吨标准煤，根据（1)中求出的线性回归方程，预测生产100吨甲产品的生产能耗比技改前降低了多少吨标准煤？‎ 附：回归直线的斜率的最小二乘法估计为：‎ 解析：（1），，‎ 所以 ‎（2）‎ ‎18. (本小题满分12分) 已知命题方程表示圆；命题双曲线的离心率，若命题“”为假命题，“ ”为真命题，求实数的取值范围.‎ ‎【答案】 或 .‎ ‎【解析】试题分析：先化简命题，得到相应的数集；再根据真值表得到的真假性，再分类进行求解．‎ 试题解析：若命题为真命题 ，则，即 整理得，解得4分 若真，则有m>0且，解得8分 因为命题为假命题，为真命题，所以中一真一假， 10分 ‎①若P真q假，则,且m 即 ‎ ‎②若P假q真，则且 即 ‎ 综上，实m的取值范围是 或 .‎ ‎19. (本小题满分12分)某班100名学生期中考试语文成绩的频率分布直方图如图所示，其中成绩分组区间是：[50,60)，[60,70)，[70,80)，[80,90)，[90,100]．‎ ‎(1)求图中a的值；‎ ‎(2)根据频率分布直方图，估计这100名学生语文成绩的平均分；‎ ‎(3)若这100名学生语文成绩某些分数段的人数(x)与数学成绩相应分数段的人数(y)之比如下表所示，求数学成绩在[50,90)之外的人数．‎ 分数段 ‎[50,60)‎ ‎[60,70)‎ ‎[70,80)‎ ‎[80,90)‎ x∶y ‎1∶1‎ ‎2∶1‎ ‎3∶4‎ ‎4∶5‎ ‎【答案】（1）0.005（2）73（3）10‎ ‎【详解】(1)由频率分布直方图知(‎2a＋0.02＋0.03＋0.04)×10＝1，解得a＝0.005．‎ ‎(2)由频率分布直方图知这100名学生语文成绩的平均分为55×0.005×10＋65×0.04×10＋75×0.03×10＋85×0.02×10＋95×0.005×10＝73(分)．‎ ‎(3)由频率分布直方图知语文成绩在[50,60)，[60,70)，[70,80)，[80,90)各分数段的人数依次为0.005×10×100＝5；0.04×10×100＝40；0.03×10×100＝30；0.02×10×100＝20．‎ 由题中给出的比例关系知数学成绩在上述各分数段的人数依次为5；40×＝20；30×＝40；20×＝25．‎ 故数学成绩在[50,90)之外的人数为100－(5＋20＋40＋25)＝10．‎ ‎20.(本小题满分12分)已知直线与抛物线交于点两点，与轴交于点，直线的斜率之积为.‎ ‎(1)证明：直线过定点，并求出定点坐标；‎ ‎(2)以为直径的圆交轴于两点，为坐标原点，求的值.‎ ‎19.(1)设直线，A(x1，y1)，B(x2，y2)‎ 由消去得，‎ 则，那么满足Δ=‎4m2‎+8n>0‎ 即，即AB过定点(4，0)………………………………………………………6分 ‎(2)∵以为直径端点的圆的方程为 设，则是方程 即的两个实根 ‎∴有 ‎∴…………………………………………………12分 ‎21. (本小题满分12分) 如图，在四棱锥中，底面是平行四边形，平面，点分别为的中点，且，.‎ ‎（1）证明：平面；‎ ‎（2）设直线与平面所成角为，，求二面角的大小.‎ 试题解析：（Ⅰ）证明：取中点，连接，‎ 因为点分别为的中点，所以 四边形为平行四边形，则又平面，平面 所以平面.‎ ‎（Ⅱ以所在的直线分别为轴、轴、轴，建立如图所示的空间直角坐标系，则设则 于是，．‎ 设平面的一个法向量为，‎ 则由．得取则所以 又，‎ ‎，平面的一个法向量为 即二面角的大小 ‎22.(本小题满分12分)已知椭圆的一焦点与的焦点重合，点在椭圆上．直线过点，且与椭圆交于两点．‎ ‎（1）求椭圆的方程；‎ ‎（2）点满足,点为坐标原点，延长线段与椭圆交于点，四边形 能否为平行四边形？若能，求出此时直线的方程，若不能，说明理由．‎ ‎【解析】（1）抛物线的焦点为，故得，‎ 解得.‎ 所以椭圆的方程为 ………………..5分 ‎（2）四边形能为平行四边形，点M为线段AB的中点．‎ 法一：（1）当直线与轴垂直时，直线的方程为满足题意；‎ 的方程为．设点的横坐标为．‎ 由得，即．‎ 四边形为平行四边形当且仅当线段与线段互相平分，即．‎ 于是．由，得满足 所以直线的方程为时，四边形为平行四边形．‎ 综上所述：直线的方程为或 . ………………………….13分 法二：（1）当直线与轴垂直时，直线的方程为满足题意；‎ ‎（2）当直线与轴不垂直时，设直线，显然，，，．‎ 将代入得，‎ 故，.‎ 四边形为平行四边形当且仅当线段与线段互相平分，即 则. ‎ 由直线，过点，得.‎ 则，即解得解得满足 所以直线的方程为时，四边形为平行四边形．‎ 综上所述：直线的方程为或 . …………………………..12分