数学文卷·2018届北京市房山区高三上学期期末考试（2018

数学文卷·2018届北京市房山区高三上学期期末考试（2018

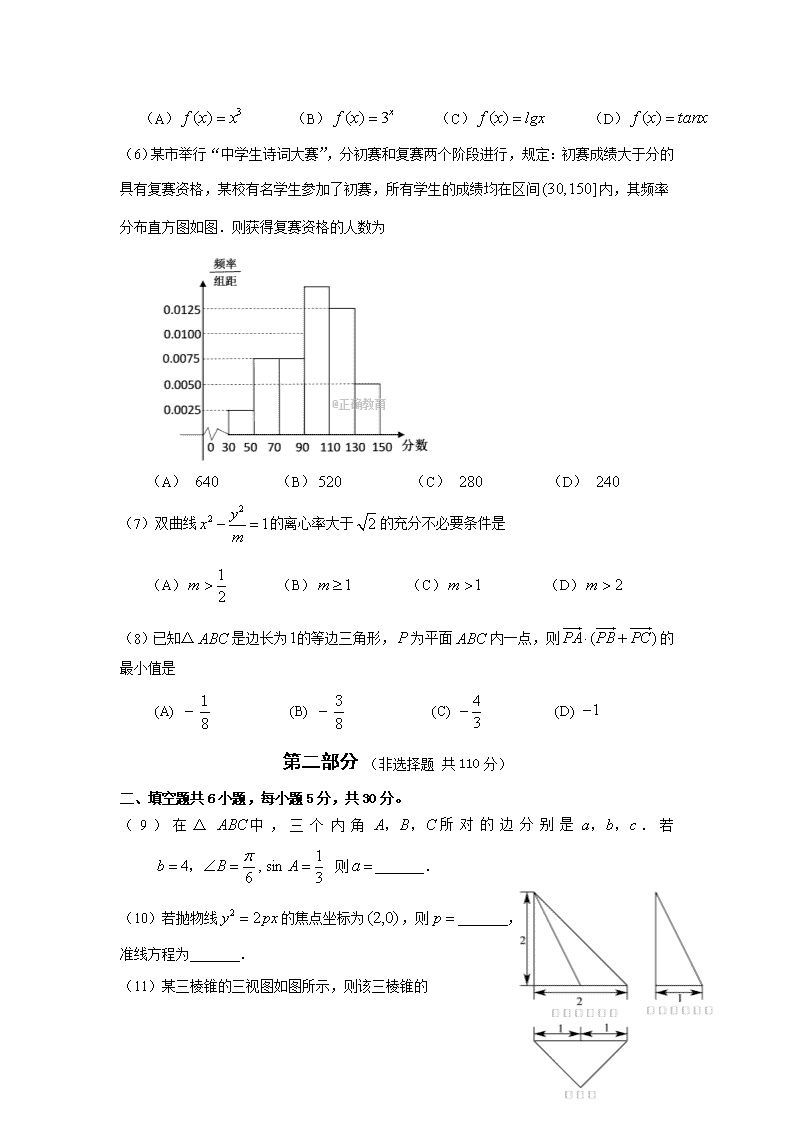
房山区2017-2018学年度第一学期期末考试试卷 高三年级数学学科（文）‎ 本试卷共5页，150分。考试时长120分钟。考生务必将答案答在答题纸上，在试卷上作答无效。考试结束后，将本试卷和答题纸一并交回。‎ 第一部分 （选择题 共40分）‎ 一、选择题共8小题，每小题5分，共40分。在每小题列出的四个选项中，选出符合题目要求的一项。‎ ‎（1）若集合，，则集合等于 ‎（A） （B） （C） （D）‎ ‎（2）在复平面内，复数在复平面中对应的点在 ‎（A）第一象限 （B）第二象限 （C）第三象限 （D）第四象限 ‎（3）若变量满足约束条件则的最大值为 ‎（A） （B） （C） （D）‎ ‎（4）某程序的框图如图所示， 执行该程序，若输入的为，则输出的的值分别为 ‎ ‎（A） ‎ ‎（B）‎ ‎（C） ‎ ‎（D）‎ ‎（5）下列函数中，满足且在定义域内是单调递增函数的是 ‎（A） （B） （C） （D）‎ ‎（6）某市举行“中学生诗词大赛”，分初赛和复赛两个阶段进行，规定：初赛成绩大于分的具有复赛资格，某校有名学生参加了初赛，所有学生的成绩均在区间内，其频率分布直方图如图．则获得复赛资格的人数为 ‎（A） （B） （C） （D） ‎ ‎（7）双曲线的离心率大于的充分不必要条件是 ‎（A） （B） （C） （D）‎ ‎（8）已知△是边长为的等边三角形，为平面内一点，则的最小值是 ‎(A) (B) (C) (D) ‎ 第二部分 （非选择题 共110分）‎ 二、填空题共6小题，每小题5分，共30分。‎ ‎（9）在△中，三个内角所对的边分别是．若 则 ．‎ ‎（10）若抛物线的焦点坐标为，则 ，准线方程为 ．‎ ‎（11）某三棱锥的三视图如图所示，则该三棱锥的 体积为 ．‎ ‎（12）如果直线把圆的面积分成相等的两部分．则________．‎ ‎（13）已知函数则=_______，若函数，则的零点个数为_______．‎ ‎（14）有三张卡片，分别写有和，和，和. 甲，乙，丙三人各取走一张卡片，甲看了乙的卡片后说：“我与乙的卡片上相同的数字不是”，乙看了丙的卡片后说：“我与丙的卡片上相同的数字不是”，丙说：“我的卡片上的数字之和不是”，若这三个人的说法都与事实相符，则甲的卡片上的数字是_______.‎ 三、解答题共6小题，共80分。解答应写出文字说明、演算步骤或证明过程。‎ ‎（15）（本小题分）‎ 已知函数．‎ ‎（Ⅰ）求函数的最小正周期；‎ ‎（Ⅱ）求函数在区间上的值域．‎ ‎（16）（本小题分）‎ 已知等差数列中，，．‎ ‎（Ⅰ）求数列的通项公式；‎ ‎（Ⅱ）设，求数列的前项和．‎ ‎（17）（本小题分）‎ 为加速京津冀一体化的旅游发展，以倡导亲子游览，增进和谐家庭为目的，由中国关心下一代工作委员会事业发展中心发起的北京亲子年票京津冀跨年版,共收入京津冀多个亲子游玩学习的好去处，年票单价元．某一旅游公司工作人员为了考察年票的使用情况，进行了抽样调查，各地区销售数量如下表所示．拟采用分层抽样的方法抽出容量为的样本．‎ 地区 北京 天津 河北 数量 ‎（Ⅰ）求这张年票中分别来自三个地区的年票数量；‎ ‎（Ⅱ）若在这张年票中随机抽取张，求至少有张来自于北京的概率；‎ ‎（Ⅲ）为迎接北京冬奥会，年票中特提供了多样化选择的平台，有十渡爱琴海滑雪场(房山)，陶然亭冰雪嘉年华（西城），八达岭滑雪场（延庆），钓鱼岛滑雪场（怀柔），门票价格分别是元，元，元, 元，年票规则是只允许使用一次．假设一名顾客在年票有效期内只在这四个滑雪场选择两个场所游玩，请回答去哪两个滑雪场更划算（只写结论）.‎ ‎（18）（本小题分）‎ 如图几何体中，是正方形，，，，，.‎ A B C D MN ‎（Ⅰ）求证：平面；‎ ‎（Ⅱ）求证：平面； ‎ ‎（Ⅲ）求三棱锥的体积.‎ ‎（19）（本小题分）‎ 已知椭圆的左顶点为，且过点.‎ ‎（Ⅰ）求椭圆的标准方程及离心率；‎ ‎（Ⅱ）若直线交椭圆于．‎ ‎（i）求证：；‎ ‎（ii）若△的面积为，求的值．‎ ‎（20）（本小题分）‎ ‎ 已知函数．‎ ‎（Ⅰ）当时，求曲线在点处的切线方程；‎ ‎（Ⅱ）若，都有成立，求的取值范围；‎ ‎（Ⅲ）当时，设,求在区间上的最大值．‎ 房山区2017-2018学年度第一学期期末考试试卷答案 高三年级数学学科（文）‎ 一、选择题共8小题，每小题5分，共40分。在每小题列出的四个选项中，选出符合题目要求的一项。‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ 答案 ‎（A）‎ ‎（A）‎ ‎（C）‎ ‎（D）‎ ‎（B）‎ ‎（B）‎ ‎（D）‎ ‎（B）‎ 二、填空题共6小题，每小题5分，共30分。‎ ‎（9） （10） （11） （12） （13） （14）‎ 三、解答题共6小题，共80分。解答应写出文字说明、演算步骤或证明过程。‎ ‎ (15)解：（Ⅰ）‎ ‎ ‎ ‎ …………………7分 ‎（Ⅱ）由（Ⅰ）得．‎ 因为，所以， ‎ 所以，因此，‎ 所以的值域为． …………………13分 ‎（16）解：（Ⅰ）设等差数列的首项为，公差为，则 解得．‎ 所以． …………………7分 ‎（Ⅱ）由（I）可得 所以． …………………13分 ‎（17）解：（Ⅰ）‎ ‎ ，，‎ 所以，来自北京、天津、河北三个地区的年票数量分别是.‎ ‎（Ⅱ）来自北京的年票记作；来自天津的年票记作；来自河北的年票记作.‎ 共种，其中至少有张来自于北京的年票共有12种。‎ 故至少有张来自于北京的概率 ‎(Ⅲ) 选择去陶然亭冰雪嘉年华（西城）和八达岭滑雪场（延庆）更划算 ‎ (18)解：（Ⅰ）在正方形中，；‎ 又，；‎ ‎ …………………5分 ‎（Ⅱ）四边形是正方形 ‎，，，‎ ‎，‎ ‎，‎ ‎ …………………10分 ‎ (Ⅲ) ‎ ‎ ‎ ‎ …………………14分 ‎（19）解：（Ⅰ）由题：‎ 又过点（），‎ ‎ …………………5分 ‎ ‎ ‎（Ⅱ）（1）由题 整理得：‎ ‎ …………………9分 （2） 由题，直线：恒过.设直线与x轴交于点M，则M ‎==‎ 或 ‎ …………………14分 ‎(20)解：(I)当时， ‎ 所以.‎ ‎ 所以，切点为.‎ ‎ 所以曲线在点处的切线方程为即 ‎ ‎…………………4分 ‎（Ⅱ）定义域为 设 令得 当变化时，，的变化如下表 ‎－‎ ‎0‎ ‎＋‎ ‎↘‎ ‎↗‎ 所以. ………………9分 所以 ‎（Ⅲ）因为，,令,则 当时, ,,为减函数 所以的最大值为 当时, 时 ‎+‎ ‎ 0‎ ‎ -‎ ‎↗‎ ‎ 极大值 ‎↘ ‎ 所以的最大值为 当时, 时，恒成立，为增函数 所以的最大值为 ………………13分