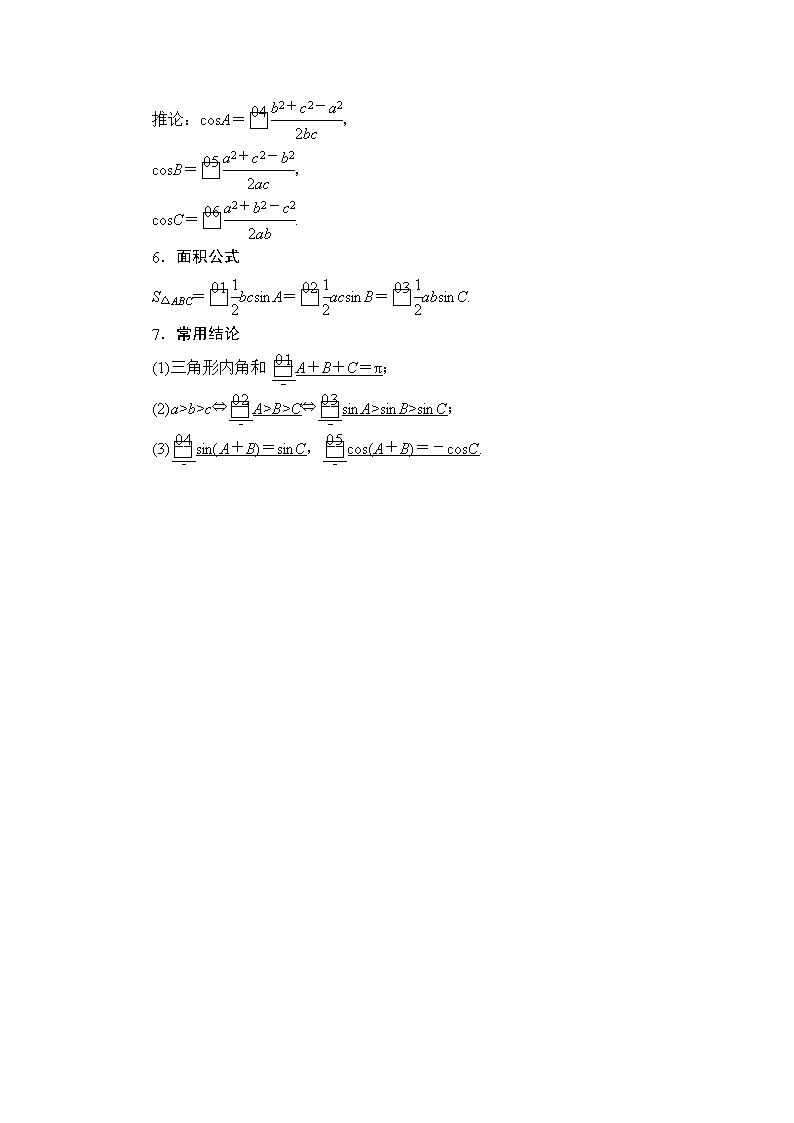高考数学二轮复习教案：第二编 专题二 第2讲 三角恒等变换与解三角形

高考数学二轮复习教案：第二编 专题二 第2讲 三角恒等变换与解三角形

第2讲　三角恒等变换与解三角形 ‎「考情研析」　　正弦定理、余弦定理以及解三角形问题是高考的必考内容，主要考查：1.边和角的计算．　2.三角形形状的判断．　3.面积的计算．　4.有关参数的范围问题．由于此内容应用性较强，与实际问题结合起来进行命题将是今后高考的一个关注点，不可轻视.‎ 核心知识回顾 ‎1.两角和与差的正弦、余弦、正切公式 sin(α±β)＝sinαcosβ±cosαsinβ；‎ cos(α±β)＝cosαcosβ∓sinαsinβ；‎ tan(α±β)＝.‎ ‎2．二倍角的正弦、余弦、正切公式 sin2α＝2sinαcosα；‎ cos2α＝cos2α－sin2α＝2cos2α－1＝1－2sin2α；‎ tan2α＝；‎ cos2α＝，sin2α＝.‎ ‎3．辅助角公式 asinα＋bcosα＝ sin(α＋φ).‎ ‎4．正弦定理 ＝＝＝2R(2R为△ABC外接圆的直径)．‎ 变形：a＝2RsinA，b＝2RsinB，c＝2RsinC.‎ sinA＝，sinB＝，sinC＝.‎ a∶b∶c＝sinA∶sinB∶sinC.‎ ‎5．余弦定理 a2＝b2＋c2－2bccosA，b2＝a2＋c2－2accosB，c2＝a2＋b2－2abcosC.‎ 推论：cosA＝，‎ cosB＝，‎ cosC＝.‎ ‎6．面积公式 S△ABC＝bcsinA＝acsinB＝absinC.‎ ‎7．常用结论 ‎(1)三角形内角和A＋B＋C＝π；‎ ‎(2)a>b>c⇔A>B>C⇔sinA>sinB>sinC；‎ ‎(3)sin(A＋B)＝sinC，cos(A＋B)＝－cosC.‎ 热点考向探究 考向1 三角恒等变换与求值 例1　(1)已知α为第一象限角，cosα＝，则 ＝(　　)‎ A. B． C． D．－ 答案　C 解析　∵cosα＝且α为第一象限角，∴sinα＝，sin2α＝2sinαcosα＝2××＝，cos2α＝2cos2α－1＝2×2－1＝－，∴＝＝＝.‎ ‎(2)已知θ∈(0，π)，且sin＝，则tan2θ＝(　　)‎ A. B． C．－ D． 答案　C 解析　∵sin＝(sinθ－cosθ)＝，∴sinθ－cosθ＝.∵θ∈(0，π)，且sin2θ＋cos2θ＝1，‎ ‎∴∴tanθ＝，tan2θ＝＝－.‎ ‎(3)(2019·四川德阳高三第二次诊断)已知α为锐角，且tanα＝，则cos＝(　　)‎ A．－ B．－ C． D． 答案　A 解析　cos＝－sin2α＝－2sinαcosα ‎＝＝＝－.‎ ‎(1)三角恒等变换的常用技巧是“化异为同”，即“化异名为同名”“化异次为同次”“化异角为同角”，其中涉及sin2，cos2时，常逆用二倍角余弦公式降幂．‎ ‎(2)常见的“变角”技巧：α＝(α＋β)－β＝β－(β－α)，α＝[(α＋β)＋(α－β)]，＋α＝－，α＝－等，使用“变角”技巧时，应根据已知条件中的角，选择恰当变角技巧．‎ ‎1．在△ABC中，若tanAtanB＝tanA＋tanB＋1，则cosC的值为(　　)‎ A．－ B． C． D．－ 答案　B 解析　由tanAtanB＝tanA＋tanB＋1，可得＝－1，即tan(A＋B)＝－1.又因为A，B是△ABC的内角，即A＋B∈(0，π)，所以A＋B＝，易知C＝，cosC＝.‎ ‎2．(2019·辽宁抚顺高三一模)已知函数f(x)＝sinx－cos，若在区间上f(x)≥a恒成立，则实数a的最大值是(　　)‎ A．－ B．－ C． D． 答案　A 解析　函数f(x)＝sinx－cos＝sinx－cosx＝sin，由于0≤x≤，故－≤x－≤，－≤sin≤.当x＝0时，函数的最小值为－.由于在区间上f(x)≥a恒成立，故a≤－，所以a的最大值为－.故选A.‎ ‎3．已知tan＝，且－<α<0，则等于(　　)‎ A．－ B．－ C．－ D． 答案　A 解析　由tan＝＝，得tanα＝－.又－<α<0，所以sinα＝－.故＝＝2sinα＝－.‎ 考向2 正弦定理与余弦定理的应用 例2　(2019·辽宁抚顺高三一模)已知a，b，c分别是△ABC的三个内角A，B，C的对边，若a＝10，角B是最小的内角，且3c＝4asinB＋3bcosA.‎ ‎(1)求sinB的值；‎ ‎(2)若c＝14，求b的值．‎ 解　(1)由3c＝4asinB＋3bcosA且A＋B＋C＝π，由正弦定理得3sinC＝4sinAsinB＋3sinBcosA，即3sin(A＋B)＝4sinAsinB＋3sinBcosA，由于00，整理可得3cosB＝4sinB，又sinB>0，所以sinB＝.‎ ‎(2)因为角B是最小的内角，所以00，所以AD＝3.‎ 真题押题 ‎『真题模拟』‎ ‎1．(2019·山东聊城高三一模)设函数f(x)＝sinx－cosx，若对于任意的x∈R，都有f(2θ－x)＝f(x)，则sin＝(　　)‎ A. B．－ C． D．－ 答案　B 解析　f(x)＝sinx－cosx＝sin，由f(2θ－x)＝f(x)，得x＝θ是函数f(x)的对称轴，得θ－＝＋kπ，k∈Z，得θ＝＋kπ，k∈Z.∴sin＝sin＝sin＝－.故选B.‎ ‎2．(2018·全国卷Ⅲ)△ABC的内角A，B，C的对边分别为a，b，c.若△ABC的面积为，则C＝(　　)‎ A. B． C． D． 答案　C 解析　由题可知S△ABC＝absinC＝，所以a2＋b2－c2＝2absinC.由余弦定理得a2＋b2－c2＝2abcosC，所以sinC＝cosC.∵C∈(0，π)，∴C＝.故选C.‎ ‎3．(2019·全国卷Ⅱ)已知α∈，2sin2α＝cos2α＋1，则sinα＝(　　)‎ A. B． C． D． 答案　B 解析　由2sin2α＝cos2α＋1，得4sinαcosα＝2cos2α.‎ 又∵α∈，∴tanα＝，∴sinα＝.故选B.‎ ‎4．(2019·河南顶级名校高三四模)已知α∈，β∈，sin(2α＋β)＝sinβ，cosβ的最小值为(　　)‎ A. B． C． D． 答案　A 解析　因为sin(2α＋β)＝sinβ，即sin[(α＋β)＋α]＝sin[(α＋β)－α]，则sin(α＋β)cosα＋cos(α＋β)sinα＝[sin(α＋β)cosα－cos(α＋β)sinα]，有sin(α＋β)cosα＝5cos(α＋β)sinα⇒tan(α＋β)＝5tanα，即＝5tanα，那么tanβ＝＝，∵α∈，β∈，∴tanα>0，tanβ>0，∴tanβ≤＝，当5tanα＝即tanα＝时等号成立．因此tan2β＝＝≤，即cos2β≥，又β∈‎ eq lc( c)(avs4alco1(0，f(π,2)))，cosβ>0⇒cosβ≥.故选A.‎ ‎5．(2018·全国卷Ⅱ)已知sinα＋cosβ＝1，cosα＋sinβ＝0，则sin(α＋β)＝______.‎ 答案　－ 解析　解法一：因为sinα＋cosβ＝1，cosα＋sinβ＝0，所以(1－sinα)2＋(－cosα)2＝1，所以sinα＝，cosβ＝，因此sin(α＋β)＝sinαcosβ＋cosαsinβ＝×－cos2α＝－1＋sin2α＝－1＋＝－.‎ 解法二：由(sinα＋cosβ)2＋(cosα＋sinβ)2＝1，得2＋2sin(α＋β)＝1，所以sin(α＋β)＝－.‎ ‎6．(2019·浙江高考)在△ABC中，∠ABC＝90°，AB＝4，BC＝3，点D在线段AC上．若∠BDC＝45°，则BD＝________，cos∠ABD＝________.‎ 答案　　 解析　如图，易知sin∠C＝，‎ cos∠C＝.在△BDC中，由正弦定理可得＝，‎ ‎∴BD＝＝＝.由∠ABC＝∠ABD＋∠CBD＝90°，可得cos∠ABD＝cos(90°－∠CBD)＝sin∠CBD＝sin[π－(∠C＋∠BDC)]＝sin(∠C＋∠BDC)＝sin∠C·cos∠BDC＋cos∠C·sin∠BDC＝×＋×＝.‎ ‎『金版押题』‎ ‎7．已知sinx＋cosx＝，则cos＝(　　)‎ A．－ B． C．－ D． 答案　B 解析　sinx＋cosx＝2＝2＝2cos＝，‎ 即cos＝.‎ ‎8．在△ABC中，角A，B，C所对的边分别是a，b，c，若＝，则cosB＝(　　)‎ A．－ B． C．－ D． 答案　B 解析　在△ABC中，由正弦定理，得＝＝1，‎ ‎∴tanB＝，又B∈(0，π)，∴B＝，cosB＝.故选B.‎ 配套作业 一、选择题 ‎1．在平面直角坐标系xOy中，已知角α的顶点与原点O重合，始边与x轴的非负半轴重合，终边上一点M的坐标为(，1)，则cos的值是(　　)‎ A．－ B．0‎ C． D．1‎ 答案　B 解析　由已知得sinα＝，cosα＝，所以cos＝cosα－sinα＝0.‎ ‎2. (2019·贵州凯里第一中学模拟)如图，是我国古代数学家赵爽的弦图，它是由四个全等的直角三角形与一个小正方形拼成的一个大正方形，如果大正方形的面积为225，小正方形的面积为9，直角三角形较小的锐角为α，则sin2α＝(　　)‎ A. B． C． D． 答案　D 解析　∵大正方形的面积为225，小正方形的面积为9，∴大正方形的边长为15，小正方形的边长为3.设四个全等的直角三角形的长直角边为x，则短直角边为x－3，由勾股定理得x2＋(x－3)2＝152，解得x＝12，α为直角三角形较小的锐角，所以sinα＝，cosα＝，所以sin2α＝2sinαcosα＝.‎ ‎3．在△ABC中，角A，B，C的对边分别是a，b，c.若 a＝b，A＝2B，则cosB＝(　　)‎ A. B． C． D． 答案　B 解析　∵a＝b，由正弦定理，得sinA＝sinB.①‎ 又∵A＝2B，∴sinA＝sin2B，sinA＝2sinBcosB.②‎ 由①②且角B为△ABC的内角得cosB＝.‎ ‎4．(2019·内蒙古呼和浩特市3月质检)在平面直角坐标系中，角α的终边过P(－2,1)，则cos2α－sin2α的值为(　　)‎ A. B． C． D． 答案　B 解析　∵在平面直角坐标系中，角α的终边过P(－2,1)，∴tanα＝＝－，则cos2α－sin2α＝＝＝，故选B.‎ ‎5．(2019·四川德阳第二次模拟)在△ABC中，BD是AC边上的高，A＝，cos∠ABC＝－，则＝(　　)‎ A. B． C． D． 答案　A 解析　∵cos∠ABC＝－，∴sin∠ABC＝＝，sinC＝sin＝(sin∠ABC＋cos∠ABC)＝，∵BD是AC边上的高，∴BD＝BCsinC＝BC，‎ 如图，由正弦定理可知＝，即AC＝BC，∴＝＝，故选A.‎ ‎6．如图，在△ABC中，B＝45°，D是BC边上一点，AD＝5，AC＝7，DC＝3，则AB＝(　　)‎ A. B． C． D． 答案　A 解析　在△ACD中，由余弦定理可得cosC＝＝，则sinC＝.在△ABC中，由正弦定理可得＝，则AB＝，选A.‎ ‎7．(2019·河南信阳高三模拟)已知函数f(x)＝2sinxcosx－2cos2x＋1，且y＝f(x)的图象沿x轴方向平移m个单位后所得的图象关于坐标原点对称，则|m|的最小值为(　　)‎ A. B． C． D． 答案　C 解析　f(x)＝2sinxcosx－2cos2x＋1＝sin2x－cos2x＝2sin，将y＝f(x)的图象向左平移m个单位(若m<0，则为向右平移－m个单位)，得到g(x)＝2sin，因为平移后图象关于点(0,0)对称，将(0,0)代入g(x)，得sin＝0，可得2m－＝kπ，k∈Z，m＝＋，k∈Z，则|m|的最小值为.故选C.‎ 二、填空题 ‎8．已知cos＋sinα＝，则cos的值是________．‎ 答案　－ 解析　∵cos＋sinα＝cos＝，‎ ‎∴cos＝2cos2－1＝－.‎ ‎9．(2019·辽宁辽南协作体高三一模)已知cosα＝，α∈，则的值为________．‎ 答案　－ 解析　由cosα＝，α∈，得sinα＝－＝－，∴＝＝‎ eq f(cosα,sinα)＝＝－.‎ ‎10．在△ABC中，内角A，B，C的对边分别是a，b，c，若sin2A－sin2B＝sinBsinC，sinC＝2sinB，则A＝________.‎ 答案　30°‎ 解析　根据正弦定理可得a2－b2＝bc，c＝2b，解得a＝b.根据余弦定理cosA＝ ‎＝＝，得A＝30°.‎ ‎11．已知不等式3sincos＋cos2－－m≤0对任意的－≤x≤恒成立，则实数m的取值范围是________．‎ 答案　[，＋∞)‎ 解析　依题意得，3sincos＋cos2－－m＝sin＋cos－m＝sin－m≤0在上恒成立，∴m≥sin在上恒成立，由于－≤＋≤，‎ ‎∴－≤ sin≤ ，故m≥ .‎ 三、解答题 ‎12．(2019·上海金山区第二学期质检)已知△ABC中，tanA＝，tanB＝，AB＝.求：‎ ‎(1)角C的大小；‎ ‎(2)△ABC中最小边的边长．‎ 解　(1)tanC＝tan[π－(A＋B)]＝－tan(A＋B)‎ ‎＝－＝－＝－1，所以C＝.‎ ‎(2)因为tanA0)，则在△ABD中，AD2＝AB2＋BD2－2AB·BDcosB，即＝25x2＋×49x2－2×5x××7x×，解得x＝1，所以a＝7，c＝5，故S△ABC＝ acsinB＝10.‎ 三角函数与解三角形类解答题 ‎(12分)已知函数f(x)＝sinωxcosωx－sin2ωx＋1(ω>0)的图象中相邻两条对称轴之间的距离为.‎ ‎(1)求ω的值及函数f(x)的单调递减区间；‎ ‎(2)已知a，b，c分别为△ABC中角A，B，C的对边，且满足a＝，f(A)＝1，求△ABC面积S的最大值．‎ 解题思路　(1)首先将函数解析式化为“一角一函数”的形式，然后利用函数图象中对称轴之间的距离确定函数的周期，从而求得ω的值，最后利用换元法求得函数的递减区间；(2)根据第(1)问所得，利用f(A)＝1求得角A，再根据余弦定理建立b，c的关系式，利用基本不等式求得bc的最大值，将其代入面积公式即可．‎ 解　(1)f(x)＝sin2ωx－＋1＝sin＋.(3分)‎ 因为函数f(x)的图象中相邻两条对称轴之间的距离为，所以T＝π，即＝π，所以ω＝1.(4分)‎ 所以f(x)＝sin＋.‎ 令＋2kπ≤2x＋≤＋2kπ(k∈Z)，解得＋kπ≤x≤＋kπ(k∈Z)．‎ 所以函数f(x)的单调递减区间为(k∈Z)．(6分)‎ ‎(2)由f(A)＝1得sin＝.因为2A＋∈，‎ 所以2A＋＝，得A＝.(8分)‎ 由余弦定理得a2＝b2＋c2－2bccosA，即()2＝b2＋c2－2bccos，(9分)‎ 所以bc＋3＝b2＋c2≥2bc，解得bc≤3，当且仅当b＝c时等号成立．(11分)‎ 所以S△ABC＝bcsinA≤×3×＝.‎ 故△ABC面积S的最大值为.(12分)‎ ‎1．化简：用诱导公式、和角公式、差角公式和倍角公式化简给3分．‎ ‎2．求ω值：运用三角函数的对称轴及周期性求ω值给1分．‎ ‎3．求单调区间：利用三角函数的单调区间求f(x)的单调区间给2分．‎ ‎4．求角：已知三角函数值求角给2分．‎ ‎5．建立关系式：利用余弦定理得出b，c的关系式给1分．‎ ‎6．求最值：利用基本不等式求出bc的最大值给2分．‎ ‎7．求面积最值：代入面积公式求最大值给1分．‎ ‎1．发现差异：观察角、函数运算的差异，即进行所谓的“差异分析”．‎ ‎2．寻找联系：运用相关公式，找出差异之间的内在联系．‎ ‎3．合理转化：选择恰当的公式促使差异的转化．‎ ‎4．挖掘隐含：如定义域、锐角、三角函数值的正负对角的范围的影响，将已知的三角函数值与特殊角的三角函数值比较、缩小角的范围等等．‎ ‎[跟踪训练]‎ ‎(2019·天津九校联考)(12分)在△ABC中，a，b，c分别是角A，B，C的对边，若b＝c，且2sinB＝sinA.‎ ‎(1)求sinB的值；‎ ‎(2)求cos的值；‎ ‎(3)若b＝2，求△ABC的面积．‎ 解　(1)因为2sinB＝sinA，‎ 所以2b＝a，即a＝b，(1分)‎ 所以cosB＝＝＝，(3分)‎ 因为B∈(0，π)，所以sinB＝.(4分)‎ ‎(2)由(1)可知cosB＝.(5分)‎ 因为sin2B＝2sinBcosB＝2××＝，‎ cos2B＝2cos2B－1＝2×2－1＝－.(6分)‎ 所以cos＝cos2Bcos－sin2Bsin ‎＝－×－×＝－.(8分)‎ ‎(3)因为b＝2，所以c＝2，a＝，(10分)‎ 所以S△ABC＝acsinB＝××2×＝.(12分)‎