数学理卷·2017届河南省八市重点高中高三12月联考试题（2016

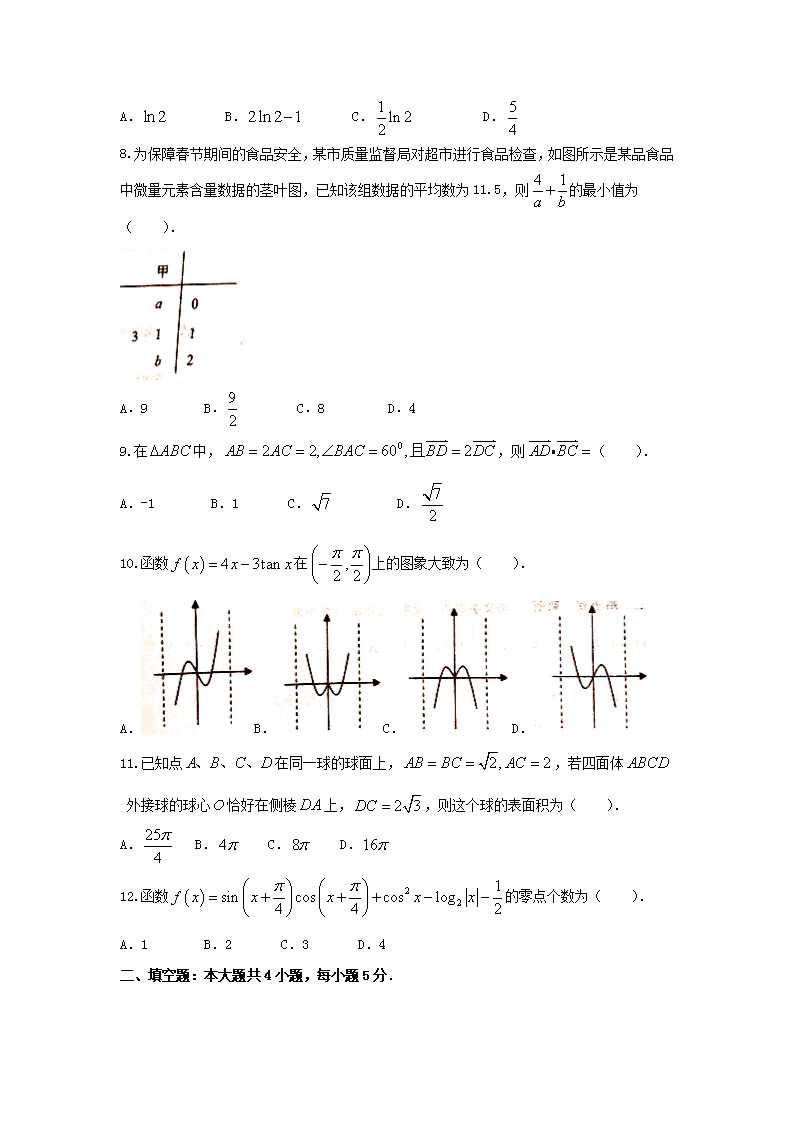
数学理卷·2017届河南省八市重点高中高三12月联考试题（2016

www.ks5u.com ‎ ‎ 理科数学 一、选择题：本大题共12小题,每小题5分,在每小题给出的四个选项中，只有一项 是符合题目要求的.‎ ‎1.设全集，集合和，则（ ）．‎ A． B． C． D．‎ ‎2.已知命题，命题“”是“”的充分不必要条件，则下列命题为真命题的是（ ）．‎ A． B． C． D．‎ ‎3.下列函数既是奇函数又在上是减函数的是（ ）．‎ A． B． C． D．‎ ‎4.在中，角所对的边分别为，若是方程的两根，且，则（ ）．‎ A．4 B． C．16 D．7‎ ‎5.已知函数，若，则（ ）．‎ A．2 B．1 C．-1 D．-2‎ ‎6.在等比数列中，，且数列的前项和，则此数列的项数等于（ ）．‎ A．4 B．7 C．6 D．5‎ ‎7.由直线，曲线及轴所围成的封闭图形的面积是（ ）．‎ A． B． C． D．‎ ‎8.为保障春节期间的食品安全，某市质量监督局对超市进行食品检查，如图所示是某品食品中微量元素含量数据的茎叶图，已知该组数据的平均数为11.5，则的最小值为（ ）．‎ A．9 B． C．8 D．4‎ ‎9.在中，，则（ ）．‎ A．-1 B．1 C． D．‎ ‎10.函数在上的图象大致为（ ）．‎ A．B．C．D．‎ ‎11.已知点在同一球的球面上，，若四面体外接球的球心恰好在侧棱上，，则这个球的表面积为（ ）．‎ A． B． C． D．‎ ‎12.函数的零点个数为（ ）．‎ A．1 B．2 C．3 D．4‎ 二、填空题：本大题共4小题，每小题5分．‎ ‎13.已知，其中为虚数单位，则____________．‎ ‎14.已知变量满足条件，且的最大值为6，则的值为____________．‎ ‎15.已知数列中，，则数列的前20项和为____________．‎ ‎16.如图是某几何体的三视图，当最大时，该几何体的体积为____________．‎ 三、解答题 ：解答应写出文字说明，证明过程或演算步骤. ‎ ‎17.（本小题满分12分）‎ 已知命题函数的值域为，命题指数函数为增函数，分别求出符合下列条件的实数的取值范围.‎ ‎（1）至少有一个是真命题；‎ ‎（2）中有且只有一个是真命题.‎ ‎18.（本小题满分12分）‎ 已知数列的前项和为，且满足. （1）求证数列是等比数列，并求数列的通项公式；‎ ‎（2）若，求数列的前项和.‎ ‎19.（本小题满分12分）‎ 在锐角三角形中，角的对边分别为，且 ‎.‎ ‎（1）求角；‎ ‎（2）若，求面积的最大值.‎ ‎20.（本小题满分12分）‎ 在如图所示的几何体中，四边形为矩形，直线平面，，点在棱上.‎ ‎（1）求证：；‎ ‎（2）若是的中点，求异面直线与所成角的余弦值；‎ ‎（3）若，求二面角的余弦值.‎ ‎21.（本小题满分12分）‎ 设公比为正数的等比数列的前项和为，已知，数列满足.‎ ‎（1）求数列和的通项公式；‎ ‎（2）若数列满足，为数列的前项和，求证：对任意.‎ ‎22.（本小题满分10分）‎ 已知函数.‎ ‎（1）设函数，讨论的单调性；‎ ‎（2）当时，恒成立，求整数的最大值.‎ 参考答案 一、选择题 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 B C C A B D A B A D D B 二、填空题 ‎13. 3 14. -3 15. 1123 16. ‎ 三、解答题 ‎17.【解析】命题为真时，合题意，时，时，为 ‎（2）中有且只有一个是真命题，有两种情况：‎ 真假时，，假真时，或，‎ ‎∴中有且只有一个真命题时，的取值范围为或或………………10分 ‎18.【解析】（1）当时，，解得，当时，‎ ‎，即 ‎，即，因为，故，所以是首项为-2，公比为2的等比数列，所以…………………………6分 ‎（2）由（1）知，所以，‎ 所以…………12分 ‎19.【解析】（1）由余弦定理得，代入已知式 ‎，‎ ‎，（*）‎ 又因为，所以化简（*）式得：，所以，因为 ‎，所以…………………………6分 ‎（2）∵，即，‎ ‎∴，‎ 所以，当且仅当时等号成立，所以，‎ 所以当时，的面积最大，最大值为………………………………12分 ‎20.【解析】（1）图（4分）‎ ‎（2）‎ 由如图所示：计算知异面直线所成的角的余弦值为……………………8分 ‎（3）因为平面，所以平面的一个法向量，由为知为的三等分点且此时.在平面中，，所以平面的一个法向量.所以，又因为二面角的大小为锐角，所以该二面角的余弦值为………………………………12分 ‎21.【解析】（1）设的公比为，则有，解得，‎ 则.‎ 即数列和的通项公式为…………………………5分 ‎（2）证明：，‎ ‎∴，‎ 易知当时，有成立，∴，‎ 令 ①‎ 则 ②‎ ‎①-②得，‎ 从而，即…………………………12分 ‎22.【解析】（1），定义域为，‎ ‎，‎ ‎①当，即时，令，∴，‎ 令，∴；‎ ‎②当，即时，恒成立，‎ 综上，当时在上单调递减，在上单调递增，‎ 当时，在上单调递增………………………5分 ‎（2）当时，恒成立，‎ 即在上恒成立，取，‎ 则，‎ 再取，则，‎ 故在上单调递增，‎ 而，‎ 故在上存在唯一实数根，‎ 故时，；时，，‎ 故，故……………12分