东城区2016届高三一模数学（文）试题及答案

东城区2016届高三一模数学（文）试题及答案

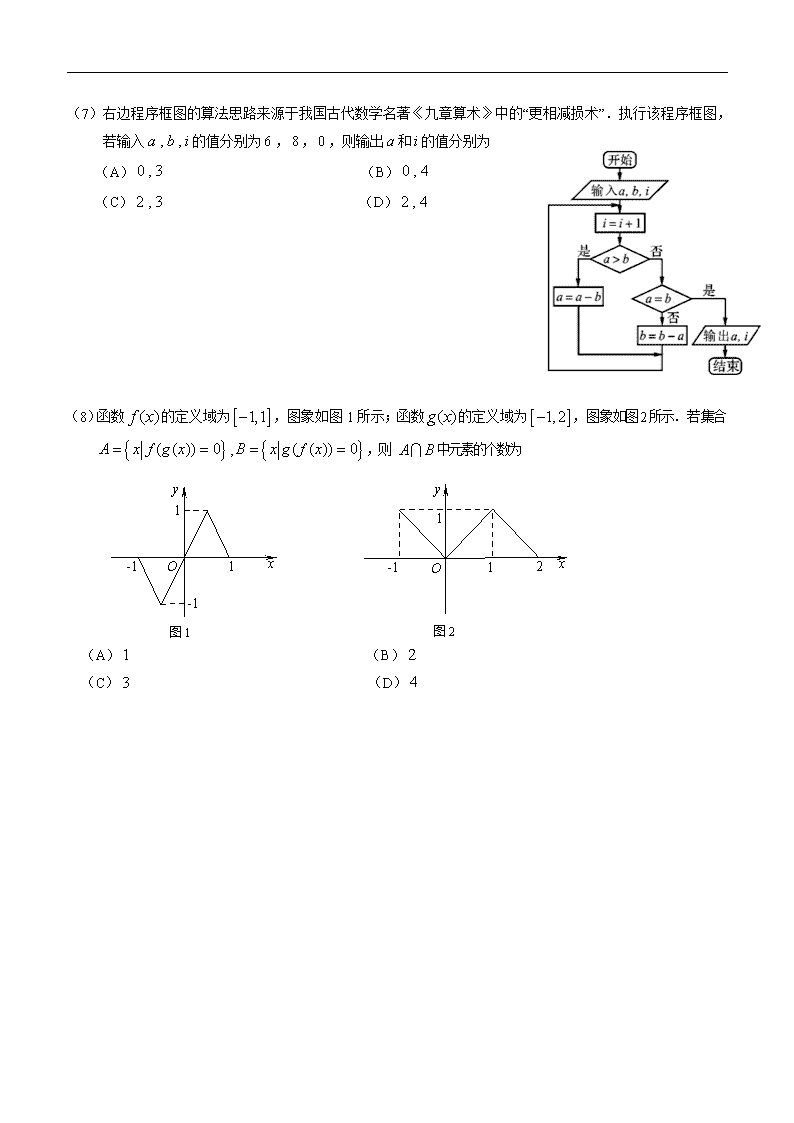
‎ ‎ 北京市东城区2015-2016学年度第二学期高三综合练习（一）‎ 数学 （文科） ‎ 本试卷共5页，共150分。考试时长120分钟。考生务必将答案答在答题卡上，在试卷上作答无效。考试结束后，将本试卷和答题卡一并交回。‎ 第Ⅰ卷（选择题 共40分）‎ 一、选择题（共8小题，每小题5分，共40分。在每小题列出的四个选项中，选出符合题目要求的一项）‎ ‎（1）若集合，，则 ‎（A） （B） ‎ ‎（C） （D）‎ ‎（2）已知直线与直线互相垂直，则 ‎（A） （B） ‎ ‎（C） （D）‎ ‎（3）已知，，，则三个数的大小关系是 ‎（A） （B） ‎ ‎（C） （D）‎ ‎（4）若满足则的最大值为 ‎（A） （B） ‎ ‎（C） （D）‎ ‎（5）已知数列的前项和，则 ‎ ‎（A） （B） ‎ ‎（C） （D）‎ ‎（6）在△中，角，，所对的边分别为，，，则“”是“”的 ‎ （A）充分而不必要条件 （B）必要而不充分条件 ‎ （C）充分必要条件 （D）既不充分也不必要条件 ‎ ‎ ‎（7）右边程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”．执行该程序框图，若输入的值分别为，，，则输出和的值分别为 ‎（A） （B） ‎ ‎（C） （D）‎ ‎（8）函数的定义域为，图象如图1所示；函数的定义域为，图象如图2所示．若集合,，则 中元素的个数为 ‎ x y ‎-1‎ O ‎1‎ ‎2‎ ‎1‎ 图2‎ x y ‎-1‎ O ‎1‎ ‎1‎ ‎-1‎ 图1‎ ‎（A） （B）‎ ‎（C） （D）‎ ‎ ‎ 第Ⅱ卷（非选择题 共110分）‎ 二、填空题共6小题，每小题5分，共30分。‎ ‎（9）若复数是实数，则 ． ‎ ‎（10）以抛物线的焦点为圆心且过坐标原点的圆的方程为 ． ‎ ‎（11）如图，在正方体ABCD－A1B‎1C1D1中，点P是上底面A1B‎1C1D1内一动点，则三棱锥P－ABC的正(主)视图与侧(左)视图的面积的比值为 ．‎ ‎（12）已知函数 ‎①若，则实数 ；‎ ‎②在①的条件下，若直线与的图象有且只有一个交点，则实数的取值范围是 ． ‎ ‎（13）如图，在矩形中，点，分别在线段，上，且满足，，若，则 ． ‎ ‎（14）每年的三月十二号是植树节，某学校组织高中个学生及其父母以家庭为单位参加“种一棵小树，绿一方净土”的义务植树活动．活动将个家庭分成两组，组负责种植棵银杏树苗，组负责种植棵紫薇树苗．根据往年的统计，每个家庭种植一棵银杏树苗用时，种植一棵紫薇树苗用时.假定两组同时开始种植,若使植树活动持续时间最短，则组的家庭数为 ，此时活动持续的时间为 ．‎ 三、解答题（共6小题，共80分。解答应写出文字说明，演算步骤或证明过程）‎ ‎（15）（本小题共13分）‎ 已知函数．‎ ‎(Ⅰ)求的最小正周期；‎ ‎(Ⅱ)求在区间上的最大值和最小值．‎ ‎（16）（本小题共13分）‎ 已知公差为正数的等差数列满足，，，成等比数列．‎ ‎(Ⅰ) 求的通项公式；‎ ‎(Ⅱ) 若，分别是等比数列的第项和第项，求使数列的前n项和的最大正整数．‎ ‎（17）（本小题共14分）‎ 如图，在四棱锥中，平面，底面是菱形，点是对角线与的交点，，，是的中点．‎ ‎(Ⅰ)求证： ∥平面；‎ ‎(Ⅱ)平面平面；‎ ‎(Ⅲ)当三棱锥的体积等于时，求的长．‎ ‎（18）（本小题共13分）‎ ‎“爱心包裹”是中国扶贫基金会依托中国邮政发起的一项全民公益活动，社会各界爱心人士只需通过中国邮政网点捐购统一的爱心包裹，就可以一对一地将自己的关爱送给需要帮助的人．某高校青年志愿者协会响应号召，组织大一学生作为志愿者，开展一次爱心包裹劝募活动．将派出的志愿者分成甲、乙两个小组，分别在两个不同的场地进行劝募，每个小组各人．爱心人士每捐购一个爱心包裹，志愿者就将送出一个钥匙扣作为纪念．以下茎叶图记录了这两个小组成员某天劝募包裹时送出钥匙扣的个数，且图中甲组的一个数据模糊不清，用x表示．已知甲组送出钥匙扣的平均数比乙组的平均数少1个．‎ 甲组 乙组 ‎(Ⅰ) 求图中的值；‎ ‎(Ⅱ) “爱心包裹”分为价值元的学习包，和价值元的“学习+生活”包，在乙组劝募的爱心包裹中元和元的比例为，若乙组送出的钥匙扣的个数即为爱心包裹的个数，求乙组全体成员劝募的爱心包裹的价值总额；‎ ‎(Ⅲ)在甲组中任选位志愿者，求他们送出的钥匙扣个数都多于乙组的平均数的概率．‎ ‎（19）（本小题共13分）‎ 已知和是椭圆：的两个焦点，且点在椭圆上．‎ ‎(Ⅰ)求椭圆的方程；‎ ‎(Ⅱ)直线与椭圆有且仅有一个公共点，且与轴和轴分别交于点，当面积取最小值时，求此时直线的方程．‎ ‎（20）（本小题共14分）‎ 已知函数，．‎ ‎(Ⅰ)若在处取得极值，求的值；‎ ‎(Ⅱ)求在区间上的最小值；‎ ‎(Ⅲ)在(Ⅰ)的条件下，若，求证：当时，恒有成立．‎ 北京市东城区2015-2016学年第二学期高三综合练习（一）‎ 数学（文科）参考答案 ‎ 一、选择题（本大题共8小题，每小题5分，共40分）‎ ‎（1）B （2）C （3）A （4）A ‎ ‎（5）D （6）C （7）D （8）C 二、填空题（本大题共6小题，每小题5分，共30分）‎ ‎（9） （10） ‎ ‎（11） （12） ‎ ‎（13） （14） ‎ 注：两个空的填空题第一个空填对得3分，第二个空填对得2分．‎ 三、解答题（本大题共6小题，共80分）‎ ‎（15）（共13分）‎ 解：（Ⅰ）‎ ‎. ……………………6分 所以的最小正周期. ……………………7分（Ⅱ）因为时，所以.‎ 于是当，即时，取得最大值；‎ 当，即时，取得最小值. ……………………13分 ‎（16）（共13分）‎ ‎ 解：（Ⅰ）设数列的公差为，‎ 由已知可得，即，‎ 整理得，解得 (舍去)或. ……………………4分 所以的通项公式为，． ……………………6分 ‎(Ⅱ) 由(Ⅰ)知，，所以等比数列的公比．‎ 于是是以为首项，以为公比的等比数列． ……………………9分 所以． ……………………11分 由，得，即，‎ 则满足不等式的最大正整数． ……………………13分 ‎（17）（共14分）‎ 证明：（Ⅰ）因为在△中，，分别是，的中点，‎ 所以∥． ‎ 又平面，平面，‎ 所以∥平面． ……………………5分 ‎(Ⅱ)因为底面是菱形，‎ 所以．‎ 因为平面，平面，‎ 所以．又，‎ 所以平面．‎ 又平面，‎ 所以平面平面． ……………………10分 ‎（Ⅲ）因为底面是菱形，且，， ‎ 所以．‎ 又，三棱锥的高为，‎ 所以，‎ 解得． ……………………14分 ‎（18）（共13分）‎ 解：（Ⅰ）由茎叶图可知乙组送出钥匙扣的平均数为．‎ 则甲组的送出钥匙扣的平均数为． ‎ 由，解得． ……………………4分 ‎(Ⅱ) 乙组送出钥匙扣的个数为，即劝募的总包裹数为，按照的比例，价值元的包裹有个，价值元的包裹有个，‎ ‎ 故所求爱心包裹的总价值元． ……………………8分 ‎（Ⅲ）乙组送出钥匙扣的平均数为个．甲组送出钥匙扣的个数分别为．‎ 若从甲组中任取两个数字，所有的基本事件为：，，，共个基本事件．‎ 其中符合条件的基本事件有，共个基本事件，‎ 故所求概率为． ……………………13分 ‎（19）（共13分）‎ 解：（Ⅰ）依题意， ，又，故. ‎ ‎ 所以.‎ 故所求椭圆的方程为. ……………………4分 ‎（Ⅱ）由消得.‎ 由直线与椭圆仅有一个公共点知， ‎ ‎，整理得． ……………………6分 由条件可得，，．‎ 所以 ． ①‎ 将代入①得．‎ 因为，所以，当且仅当，即时等号成立，‎ 有最小值．‎ ‎ 因为，所以，又，解得． ……………………11分 故所求直线方程为或． ……………………13分 ‎（20）（共14分）‎ 解：（Ⅰ）由，定义域为，‎ 得．‎ 因为函数在处取得极值，‎ 所以，即，解得．‎ 经检验，满足题意，所以． ………………………4分 ‎（Ⅱ）由（Ⅰ）得，定义域为．‎ 当时，有，在区间上单调递增，最小值为；‎ 当，由得，且．‎ 当时，，单调递减，当时，，单调递增，‎ 所以在区间上单调递增，最小值为；‎ 当时，，‎ 当时，，单调递减，当时，，单调递增，‎ 所以函数在取得最小值． ‎ 综上当时，在区间上的最小值为；‎ 当时，在区间上的最小值为． ………………9分 ‎（Ⅲ）由得．‎ 当时，，，‎ 欲证，只需证，‎ 即证，即． ………………11分 设，‎ 则．‎ 当时，，所以在区间上单调递增．‎ 所以当时，，即，‎ 故．‎ 所以当时，恒成立． ………………………..14分 ‎ ‎ ‎ ‎