内蒙古赤峰二中2019-2020学年高二上学期月考数学(理)试题
赤峰二中2018级高二上学期第二次考试
数学试题(理科)
选择题(每小题5分,共60分)
1.若,,则是的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
2.抛物线的焦点坐标是
A. (0,1) B.(1,0) C.(0, ) D.(0,2)
3.若函数有极值点, 则实数的取值范围为 ( )
4.已知点是抛物线上的一个动点,则点到点的距离与到该抛物线准线的距离之和的最小值为( )
A. B.3 C. D.
5.若函数f(x)=kx-lnx在区间(1,+∞)上单调递增,则k的取值范围是( )
A.(-∞,-2] B.(-∞,-1]
C.[1,+∞) D.[2,+∞)
6.已知点是双曲线(, )右支上一点, 是右焦点,若(是坐标原点)是等边三角形,则该双曲线离心率为( )
A. B. C. D.
7.定义域为R的函数f(x)满足f(1)=1,且f(x)的导函数f ′(x)>,则满足
2f(x)
1} D.{x|x>1}
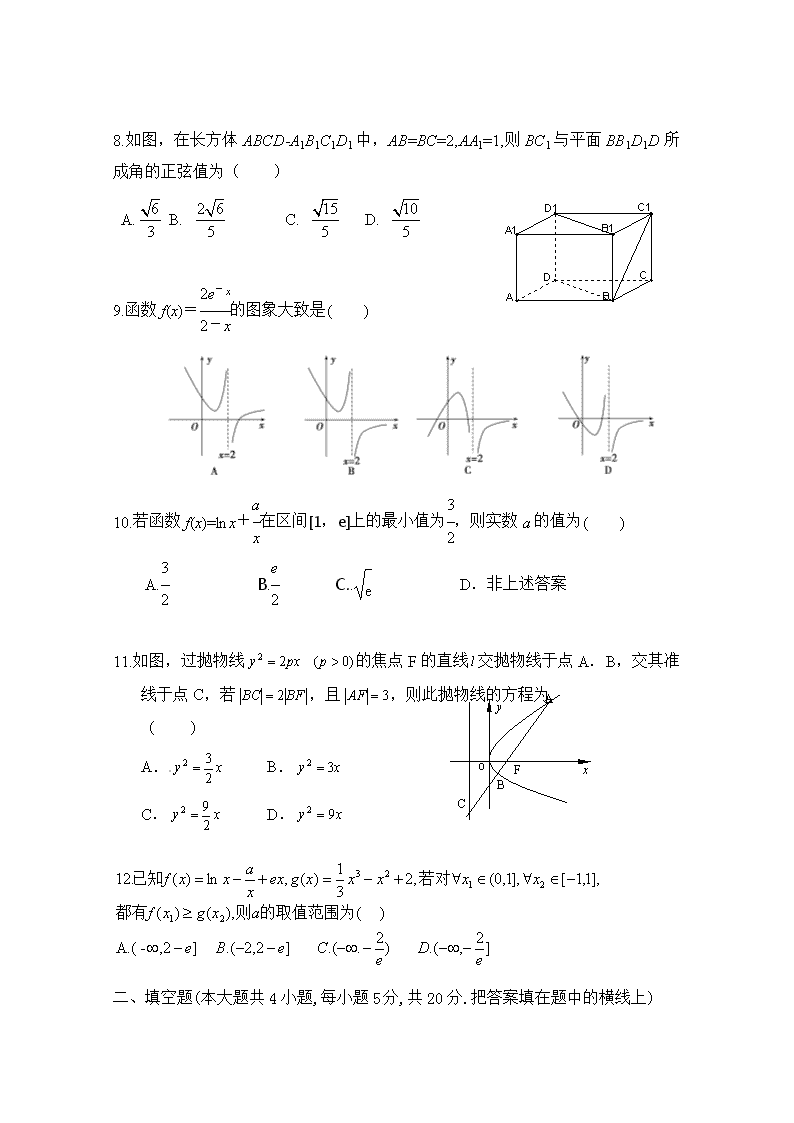
8.如图,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1,则BC1与平面BB1D1D所成角的正弦值为( )
A. B. C. D.
[来源:学#科#网]
9.函数f(x)=的图象大致是( )
10.若函数f(x)=lnx+在区间[1,e]上的最小值为,则实数a的值为( )
A. B. C.. D.非上述答案
F
x
y
A
B
C
O
11.如图,过抛物线的焦点F的直线交抛物线于点A.B,交其准线于点C,若,且,则此抛物线的方程为 ( )
A. B.
C. D. [来源:学。科。网]
二、 填空题(本大题共4小题,每小题5分,共20分.把答案填在题中的横线上)
__________.
14.
若函数的值为
15.已知直线L交椭圆 于M、N两点,椭圆与y轴的正半轴交于点B,若的重心恰好落在椭圆的右焦点F上,则直线L的方程是__________.
16已知函数有两个极值点,则的取值范围是__________
三简答题
17.(本题满分10分)已知函数
(1)求f(x)的单调区间;
(2)求f(x)在[0,3]上的最大值和最小值。
18.(本小题满分12分)D
A
C
O
B
E
如图,在四面体ABCD中,O、E分别是BD、BC的中点,
(Ⅰ)求证:平面BCD;
(Ⅱ)求AE与平面ACD所成角的正弦值.
19. (本小题满分12分已知抛物线C:上一点M(3,t)到焦点F的距离为4
(1) 求t,p的值.
(2) 过焦点F作直线L交抛物线C于A,B两点,交轴y于P点,且
,证明:为定值.
20. 如图,在直三棱柱中,,E是BC中点.AB=AC=AA1
=2(I)求证:平面
(Ⅲ)求平面与平面所成锐二面角的余弦值.
[来源:学&科&网]
21.(本题满分12分)已知椭圆(a>b>0)的焦距与椭圆的短轴长相等,且W与Ω长轴长相等,这两个椭圆在第一象限的交点为A,直线L与直线OA(O为坐标原点)垂直,且L与椭圆W交于M,N两点.
(1)求W的方程;
(2)求△MON的面积的最大值.
22.(本题满分12分)已知函数,(a>0)
(1) 讨论的单调性;
(2) 若有两个极值点,且,当恒成立时,求m的取值范围。
[来源:学科网ZXXK]
数学理科答案
一、选择题:
(1)A(2)C (3)A(4)A(5)C(6) D(7)B(8)D(9)B(10)C(11) B(12)D
二、填空题:
(13)(0,1) (14)2 (15)6x-5y-28=0 (16)(0,)
三简答题
18.
(2)
[来源:学科网ZXXK]
20.【答案】(I) 连接交于点,连接,如图所示,
由于四边形为正方形,
所以为中点,
又为中点,
所以,
又平面,平面,以平面. ………………4分
(Ⅱ)以为原点,为轴,为轴,为轴建立空间直角坐标系,如图所示,
则
,
,
设平面的法向量为,
则有所以
令则,所以是平面的一个法向量,
又平面,则是平面的一个法向量,
,
所以所求余弦值为
21.解:(1)由题意可得,∴,故W的方程为. 4分
(2)联立,得,∴,又A在第一象限,∴.
故可设l的方程为y=-3x+m.联立,得31x2-18mx+3m2-12=0,
设M(x1,y1),N(x2,y2),则,, ……7分
∴,
又O到直线l的距离为,则△MON的面积,……10分
∴,当且仅当m2=31-m2,即,满足Δ>0,故△MON的面积的最大值为. ……12分
22.(1)
所以,为减函数,所以