- 2021-06-19 发布 |
- 37.5 KB |
- 7页


申明敬告: 本站不保证该用户上传的文档完整性,不预览、不比对内容而直接下载产生的反悔问题本站不予受理。
文档介绍
高三数学二轮高考专题辅导与训练打包检测试题:专题六第3讲课时训练提能
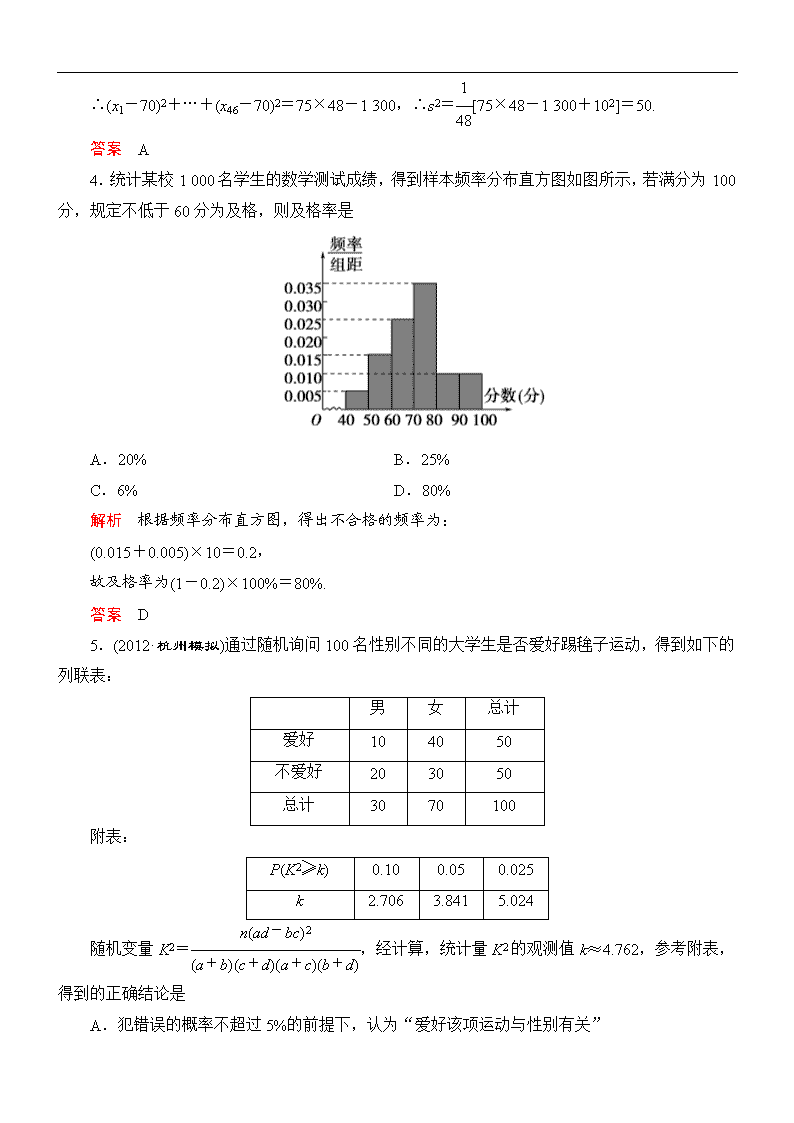
专题六 第 3 讲 统计、统计案例 课时训练提能 [限时 45 分钟,满分 75 分] 一、选择题(每小题 4 分,共 24 分) 1.(2012·淄博高三一模)某单位有青年职工 160 人,中年职工人数是老年职工人数的 2 倍,老、 中、青职工共有 430 人,为了解职工身体状况,现采用分层抽样方法进行调查,在抽取的样本中 有青年职工 32 人,则该样本中的老年职工人数为 A.16 B.18 C.27 D.36 解析 设老年职工人数为 x,则中年职工人数为 2x, ∴x+2x+160=430,∴x=90,据题意得 32 160 = y 90 ,∴y=18. 答案 B 2.(2012·惠州模拟)一个总体分为 A,B,C 三层,其个体数之比为 5∶3∶2,若用分层抽样的 方式抽取容量为 200 的样本,则应从 B 中抽取的个体数为 A.40 B.60 C.80 D.100 解析 设从 B 中抽取的个体数为 x,据题意得 x 3 = 200 5+3+2 ,∴x=60. 答案 B 3.(2012·福州模拟)某班有 48 名学生,在一次考试中统计出平均分为 70 分,方差为 75,后来 发现有 2 名同学的分数登错了,甲实得 80 分却记成了 50 分,乙实得 70 分却记成了 100 分,则更 正后平均分和方差分别是 A.70,50 B.70,75 C.70,72.5 D.65,70 解析 平均分不变. 原方差 s= 1 48[(x1-70)2+…+(x46-70)2+202+302], ∴(x1-70)2+…+(x46-70)2=75×48-1 300,∴s2= 1 48[75×48-1 300+102]=50. 答案 A 4.统计某校 1 000 名学生的数学测试成绩,得到样本频率分布直方图如图所示,若满分为 100 分,规定不低于 60 分为及格,则及格率是 A.20% B.25% C.6% D.80% 解析 根据频率分布直方图,得出不合格的频率为: (0.015+0.005)×10=0.2, 故及格率为(1-0.2)×100%=80%. 答案 D 5.(2012·杭州模拟)通过随机询问 100 名性别不同的大学生是否爱好踢毪子运动,得到如下的 列联表: 男 女 总计 爱好 10 40 50 不爱好 20 30 50 总计 30 70 100 附表: P(K2≥k) 0.10 0.05 0.025 k 2.706 3.841 5.024 随机变量 K2= nad-bc2 a+bc+da+cb+d ,经计算,统计量 K2 的观测值 k≈4.762,参考附表, 得到的正确结论是 A.犯错误的概率不超过 5%的前提下,认为“爱好该项运动与性别有关” B.在犯错误的概率不超过 5%的前提下,认为“爱好该项运动与性别无关” C.有 97.5%以上的把握认为“爱好该项运动与性别有关” D.有 97.5%以上的把握认为“爱好该项运动与性别无关” 解析 由表可知,犯错误的概率不超过 5%的前提下,认为“爱好该项运动与性别有关”,即 有 95%的把握认为“爱好该项运动与性别有关”.故选 A. 答案 A 6.(2012·泰安模拟)下列说法: ①将一组数据中的每个数据都加上或减去同一个常数后,方差恒不变; ②设有一个回归方程y ∧ =3-5x,变量 x 增加一个单位时,y 平均增加 5 个单位; ③线性回归方程y ∧ =bx+a 必过( x-, y-); ④在一个 2×2 列联表中,由计算得 K2=13.079,则有 99%的把握确认这两个变量间有关系. 其中错误的个数是 A.0 B.1 C.2 D.3 本题可以参考独立性检验临界值表 P(K2≥k) 0.5 0.40 0.25 0.15 0.10 k 0.455 0.708 1.323 2.072 2.706 P(K2≥k) 0.05 0.25 0.10 0.005 0.001 k 3.841 5.024 6.535 7.879 10.828 解析 ①③④皆正确;②错误,原因为变量 x 增加一个单位时,y 平均减少 5 个单位. 答案 B 二、填空题(每小题 5 分,共 15 分) 7.(2012·济南模拟)某企业 3 个分厂同时生产同一种电子产品,第一、二、三分厂的产量之比 为 1∶2∶1,用分层抽样方法(每个分厂的产品为一层)从 3 个分厂生产的电子产品中共取 100 件作 使用寿命的测试,由所得的测试结果算得从第一、二、三分厂取出的产品的使用寿命的平均值分 别为 980 h,1 020 h,1 032 h,则抽取的 100 件产品的使用寿命的平均值为________h. 解析 根据分层抽样原理,第一、二、三分厂抽取的产品数量分别为 25,50,25, 所以所求 100 件产品的平均寿命为 980×25+1 020×50+1032×25 100 =1 013 h. 答案 1 013 8.(2012·丰台二模)某地区恩格尔系数 y(%)与年份 x 的统计数据如下表: 年份 x 2004 2005 2006 2007 恩格尔系数 y(%) 47 45.5 43.5 41 从散点图可以看出 y 与 x 线性相关,且可得回归方程为y ∧ =bx+4 055.25,据此模型可预测 2012 年该地区的恩格尔系数(%)为________. 解析 由表可知 x-=2 005.25, y-=44.25. ∵ y-=b x-+4 055.25, 即 44.25=2 005.5b+4 055.25, ∴b=-2,∴回归方程为y ∧ =-2x+4 055.25, 令 x=2 012,得y ∧ =31.25. 答案 31.25 9.(2012·日照模拟)样本容量为 1 000 的频率分布直方图如图所示.根据样本的频率分布直方 图,计算 x 的值为________,样本数据落在[6,14)内的频数为________. 解析 4×(0.02+0.03×2+0.08+x)=1,∴x=0.09, 1 000×(4×0.08+4×0.09)=680. 答案 0.09 680 三、解答题(每小题 12 分,共 36 分) 10.某学生对其亲属 30 人的饮食习惯进行了一次调查,并用茎叶图表示 30 人的饮食指数, 如图所示.(说明:图中饮食指数低于 70 的人,饮食以蔬菜为主;饮食指数高于 70 的人,饮食以 肉类为主.) (1)根据茎叶图,帮助这位同学说明其亲属 30 人的饮食习惯; (2)根据以上数据完成如表所示的 2×2 列联表; 主食蔬菜 主食肉类 合计 50 岁以下 50 岁以上 合计 (3)能否有 99%的把握认为“其亲属的饮食习惯与年龄有关”?并写出简要分析. 附:K2= nad-bc2 a+bc+da+cb+d P(K2≥k0) 0.25 0.15 0.10 0.05 0.024 0.010 0.005 0.001 k0 1.323 2.072 2.706 3.841 5.024 6.635 7.879 10.828 解析 (1)30 位亲属中 50 岁以上的人多以食蔬菜为主,50 岁以下的人多以食肉为主. (2)列联表如表所示: 主食蔬菜 主食肉类 合计 50 岁以下 4 8 12 50 岁以上 16 2 18 合计 20 10 30 (3)K2= 30×8-1282 12×18×20×10 = 30×120×120 12×18×20×10 =10>6.635, 由附表知,有 99%的把握认为“其亲属的饮食习惯与年龄有关”. 11.某研究机构对高三学生的记忆力 x 和判断力 y 进行统计分析,所得数据如表所示: x 6 8 10 12 y 2 3 5 6 (1)请画出上表数据的散点图; (2)请根据上表提供的数据,用最小二乘法求出 y 关于 x 的线性回归方程y ∧ =bx+a; (3)试根据(2)求出的线性回归方程,预测记忆力为 9 的学生的判断力. (相关公式:b= ∑n i=1xiyi-n x-· y- ∑n i=1x2i -n x-2 ,a= y--b x-.) 解析 (1)如图所示. (2)∑4 i=1xiyi=6×2+8×3+10×5+12×6=158, x-=6+8+10+12 4 =9, y-=2+3+5+6 4 =4, ∑4 i=1x2i =62+82+102+122=344, b=158-4×9×4 344-4×92 =14 20 =0.7,a= y--bx =4-0.7×9=-2.3, 故线性回归方程为y ∧ =0.7x-2.3. (3)由回归直线方程预测,记忆力为 9 的学生的判断力约为 4. 12.以下茎叶图记录了甲、乙两组各四名同学的植树棵数.乙组记录中有一个数据模糊,无 法确认,在图中以 X 表示. 甲组 乙组 9 9 0 X 8 9 1 1 1 0 (1)如果 X=8,求乙组同学植树棵数的平均数和方差; (2)如果 X=9,分别从甲、乙两组中随机选取一名同学,求这两名同学的植树总棵数为 19 的 概率. (注:方差 s2=1 n[(x1- x-)2+(x2- x-)2+…+(xn- x-)2],其中 x-为 x1,x2,…,xn 的平均数) 解析 (1)当 X=8 时,由茎叶图可知,乙组同学的植树棵数是 8,8,9,10,所以平均数为 x-= 8+8+9+10 4 =35 4 ; 方差为 s2=1 4 8-35 4 2+ 8-35 4 2+ 9-35 4 2+ 10-35 4 2 =11 16. (2)记甲组四名同学为 A1,A2,A3,A4, 他们植树的棵数依次为 9,9,11,11; 乙组四名同学为 B1,B2,B3,B4, 他们植树的棵数依次为 9,8,9,10. 分别从甲、乙两组中随机选取一名同学, 所有可能的结果有 16 个,它们是: (A1,B1),(A1,B2),(A1,B3),(A1,B4), (A2,B1),(A2,B2),(A2,B3),(A2,B4), (A3,B1),(A3,B2),(A3,B3),(A3,B4), (A4,B1),(A4,B2),(A4,B3),(A4,B4), 用 C 表示:“选出的两名同学的植树总棵数为 19”这一事件,则 C 中的结果有 4 个,它们是: (A1,B4),(A2,B4),(A3,B2),(A4,B2), 故所求概率为 P(C)= 4 16 =1 4.查看更多