数学理卷·2018届山东省青岛二中高三上学期第二学段模块考试（2018

数学理卷·2018届山东省青岛二中高三上学期第二学段模块考试（2018

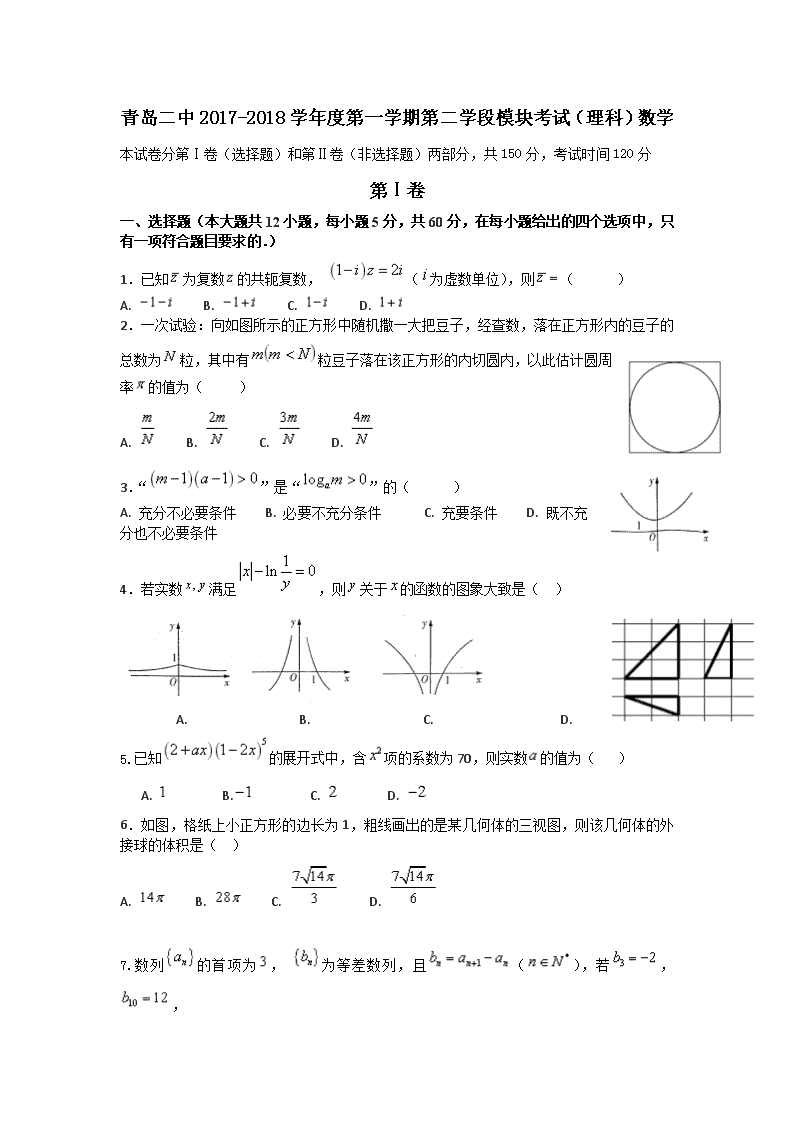
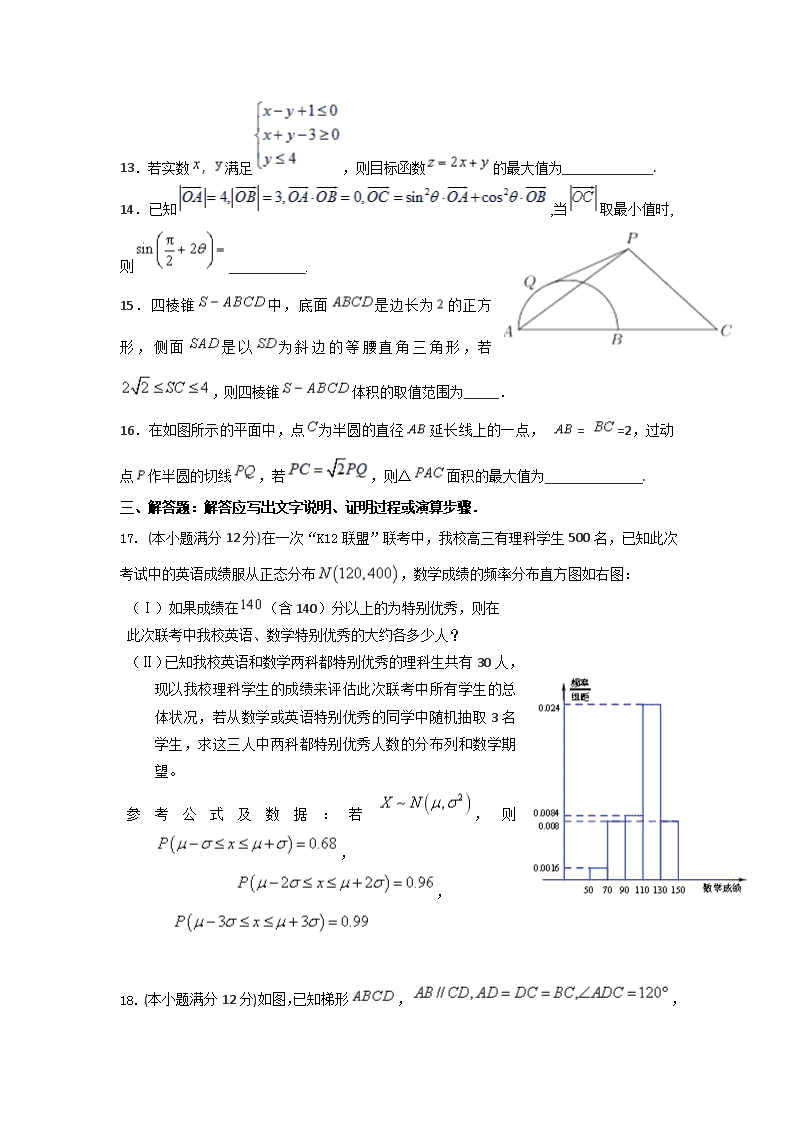
青岛二中2017-2018学年度第一学期第二学段模块考试（理科）数学 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，共150分，考试时间120分 第Ⅰ卷 一、选择题（本大题共12小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项符合题目要求的．）‎ ‎1．已知为复数的共轭复数， （为虚数单位），则（ ）‎ A. B. C. D. ‎ ‎2．一次试验：向如图所示的正方形中随机撒一大把豆子，经查数，落在正方形内的豆子的总数为粒，其中有粒豆子落在该正方形的内切圆内，以此估计圆周率的值为（ ）‎ A. B. C. D. ‎ ‎3．“”是“”的（ ）‎ A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件 ‎4．若实数满足，则关于的函数的图象大致是（ ）‎ ‎ ‎ A. B. C. D. ‎ ‎5.已知的展开式中，含项的系数为70，则实数的值为（ ）‎ A. B. C. D. ‎ ‎6．如图，格纸上小正方形的边长为1，粗线画出的是某几何体的三视图，则该几何体的外接球的体积是（ ）‎ A. B. C. D. ‎ ‎ ‎ ‎7.数列的首项为， 为等差数列，且（），若， ，‎ 则（ ）‎ A. B. C. D. ‎ ‎8.如图，在中， 是边上的点，且满足， ， ，则（ ）‎ A. B. C. D. 0‎ ‎9．已知，函数的部分图象如图所示，则函数图象的一个对称中心是（ ）‎ A. B. C. D. ‎ ‎10．直线与双曲线的渐近线交于两点，设为双曲线上任一点，若（为坐标原点），则下列不等式恒成立的是（ ）‎ A. B. C. D. ‎ ‎11．如图所示：在杨辉三角中，斜线上方箭头所连的数组成一个齿形的数列：记这个数列前项和为，则等于( ) ‎ A. 128 B. 144 C. 155 D. 164 ‎ ‎12.已知函数.正实数满足，则下述结论中正确的一项是( )‎ A. B. C. D. ‎ 第Ⅱ卷 本卷包括必考题和选考题两部分．第13~21题为必考题，每个试题考生都必须作答．第22~23题为选考题，考生根据要求作答．‎ 二、填空题：（本大题共4小题，每小题5分，共60分．把答案填在题中横线上）‎ ‎13．若实数, 满足，则目标函数的最大值为_____________.‎ ‎14．已知,当取最小值时,则___________.‎ ‎15．四棱锥中，底面是边长为的正方形，侧面是以为斜边的等腰直角三角形，若，则四棱锥体积的取值范围为_____．‎ ‎16．在如图所示的平面中，点为半圆的直径延长线上的一点， = =2，过动点作半圆的切线，若，则△面积的最大值为______________.‎ 三、解答题：解答应写出文字说明、证明过程或演算步骤．‎ ‎17. (本小题满分12分)在一次“K12联盟”联考中，我校高三有理科学生500名，已知此次考试中的英语成绩服从正态分布，数学成绩的频率分布直方图如右图：‎ ‎（Ⅰ）如果成绩在（含140）分以上的为特别优秀，则在 此次联考中我校英语、数学特别优秀的大约各多少人？‎ ‎（Ⅱ）已知我校英语和数学两科都特别优秀的理科生共有30人，现以我校理科学生的成绩来评估此次联考中所有学生的总体状况，若从数学或英语特别优秀的同学中随机抽取3名学生，求这三人中两科都特别优秀人数的分布列和数学期望。‎ 参考公式及数据：若，则，‎ ‎，‎ ‎ ‎ ‎18. (本小题满分12分)如图，已知梯形，‎ ‎， 四边形为正方形，且平面⊥平面．‎ ‎（Ⅰ）求证：平面；‎ ‎（Ⅱ）点在线段上运动，求平面与平面所成锐二面角余弦值的取值范围．‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎19．(本小题满分12分) 已知数列的前项和为，，且对任意正整数，都有 ‎，数列满足 ‎（Ⅰ）求数列，的通项公式；‎ ‎（Ⅱ）求证：‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎20. (本小题满分12分)如图，曲线由下半椭圆和部分抛物线连接而成，与的公共点为，其中的离心率为．‎ ‎（Ⅰ）求的值；‎ ‎（Ⅱ）过点的直线与，分别交于点，（均异于点），是否存在直线，使得以为直径的圆恰好过点，若存在，求出直线的方程；若不存在，请说明理由．‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎21. (本小题满分12分)已知函数， ，（其中， 为自然对数的底数， ……）.‎ ‎（Ⅰ）令，若对任意的恒成立，求实数的值；‎ ‎（Ⅱ）在（1）的条件下，设为整数，且对于任意正整数， ，求的最小值.‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ 选考部分 请考生在第22~23题中任选一题作答，如果多做，则按所做的第一题计分．作答时请写清题号 ‎22. (本小题满分10分) 选修4─4：坐标系与参数方程 在直角坐标系xOy中，曲线：‎ ‎(t为参数)．以坐标原点O为极点，x轴正半轴为极轴建立极坐标系，曲线：．‎ ‎（Ⅰ）求的普通方程与曲线的直角坐标方程，并说明方程所表示的曲线名称；‎ ‎（Ⅱ）判断曲线与曲线的位置关系，若相交，求出弦长．‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎23. (本小题满分10分) 选修4─5：不等式选讲 已知函数 ‎（Ⅰ）当时，求函数的定义域；‎ ‎（Ⅱ）若关于的不等式的解集是,求的取值范围.‎ ‎ ‎ ‎ ‎ ‎ ‎